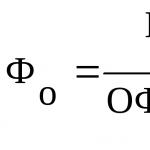ПОТРЕБЛЕНИЕ И СПРОС
2.1 Задачи
Задача № 1
Объем потребления некоторого товара домашним хозяйством
(q) в зависимости от дохода (I) описывается равенством:
Определить, при каких значениях дохода товар для
данного домашнего хозяйства является
а) низшим благом;
б) нормальным благом;
в) необходимым благом;
г) роскошным благом.
Задача № 2 Индивид потребляет два блага в количествах x и y соответственно. Согласуются ли приведенные ниже функции полезности с аксиомами потребительских предпочтений? (да/нет)
а) U(x, y) = x2 + y 2 ;
в) U(x, y) = +.
xy Задача № 3 Предпочтения индивида характеризуются предельными нормами замещения MRSxy = 2, MRSxz = 0.8. Найти предельные нормы замещения а) MRSyx, б) MRSzx, в) MRSyz, г) MRSzy.
16 Часть II.
Задача № 4 Домашнее хозяйство потребляет два блага в количествах x и y; его предпочтения описываются функцией полезности U(x, y). Найти функцию спроса домашнего хозяйства, если
а) U(x, y) = x3y2;
б) U(x, y) = xy.
Задача № 5 Предпочтения двух индивидов описываются функциями полезности xy U1 (x, y) = U2 (x, y) = ln x + ln y ln(x + y).
x+y Различаются ли предпочтения этих индивидов?
Задача № 6 Рассмотрим модель, в которой предпочтения потребителя относятся не к продуктам, а к характеристикам, которыми продукты обладают (модель Ланкастера). Допустим, что рассматривается множество продуктов, обладающих двумя характеристиками (X и Y).
Обозначим (xi, yi) количественные меры соответствующих характеристик в единице i-го продукта, причем простоты ради в качестве единицы каждого продукта принимается количество продукта, приобретаемое за одну денежную единицу. Будем считать, что предпочтения в пространстве Потребление и спрос. 17 характеристик удовлетворяют тем же аксиомам, что и предпочтения в пространстве благ в традиционной теории.
В таблице (см. выше) приведены данные по шести различным продуктам. Какие из них не имеют перспектив быть проданными на рынке?
Задача № 7 Домашнее хозяйство потребляет два блага, X и Y, в количествах x и y; его доход I = 60, а предпочтения опиxy сываются функцией полезности U(x, y) =.
а) Найти объемы спроса на каждое из благ при ценах благ pX = 9, pY = 4.
Задача № 8 Домашнее хозяйство потребляет два блага, X и Y, в количествах x и y; его предпочтения описываются функцией полезности U(x, y) = x + y. Известен доход: I = 60.
а) Найти объемы спроса на каждое из благ при ценах благ pX = 10, pY = 5.
б) Определить зависимости объемов спроса на каждое из благ от цен и дохода.
в) Определить характер взаимозависимости благ в потреблении.
Задача № 9
– – –
б) Определить зависимости от дохода объемов спроса на каждое из благ.
Задача № 10 Индивид потребляет два блага, X и Y, в количествах x и y соответственно.
Функция полезности индивида:
U = ax + by + xy, a 0, b 0.
а) Пусть a = 10, b = 25. Определить объемы потребления благ, если цены благ pX = 5, pY = 2 при доходе индивида I = 200;
б) то же при доходе индивида I = 100;
в) при каких соотношениях дохода и цен оптимум потребителя будет внутренним (x 0, y 0)?
Задача № 11
Домашнее хозяйство приобретает благо X, производимое естественной монополией, по цене pX = 10 в количестве x = = 5. Государство, регулирующее цену продукта естественной монополии, сочло целесообразным повысить цену до pX = = 14 и выплачивать домашнему хозяйству компенсацию в размере (pX – pX) x = 20.
а) Изменилось ли благосостояние домашнего хозяйства, и если да, то в какую сторону?
б) Проверить утверждение на следующем примере: домашнее хозяйство кроме блага X потребляет еще одно благо, Y, цена которого pY = 1 не изменилась; доход домашнего хозяйства I = 100, а функция полезности U(x, y) = xy.
Задача № 12 Классификация благ, основанная на кривых Энгеля, учитывает изменения доли дохода, направленной на покупку рассматриваемого блага, в зависимости от изменения дохода.
Докажите следующие утверждения:
Потребление и спрос. 19 если доля дохода, направляемая на покупку данного блага, увеличивается с ростом дохода, то эластичность объема потребления по доходу больше единицы;
если доля дохода, направляемая на покупку данного блага, уменьшается с ростом дохода, то эластичность объема потребления по доходу меньше единицы.
Задача № 13
Домашнее хозяйство потребляет три блага, X, Y и Z. Их доли в расходах составляют соответственно sX = 50%, sY = = 30%, sZ = 20%. Известны эластичности по доходу объемов потребления благ X и Y: EI[x] = 2, EI[y] = 0.6.
а) Найти эластичность объема потребления блага Z по доходу.
б) Определить, к какому типу относится каждое из благ.
Задача № 14 Докажите утверждение: если среди благ, потребляемых домашним хозяйством, есть хотя бы одно низшее, то среди них имеется также хотя бы одно роскошное.
Задача № 15 Телефонная компания предлагает потребителям услуг на выбор два варианта тарифов: (а) 4 ед./мин без абонентской платы; (б) 2 ед./мин и абонентская плата 20 ед.
Какой из тарифов выберет каждый из следующих потребителей:
1) функция полезности U1 = x0.5y0.5, доход I1 = 100 ед.;
2) функция полезности U2 = x0.25y0.75, доход I2 = 100 ед.;
3) функция полезности U3 = x0.25y0.75, доход I3 = 200 ед.
Здесь x - количество (в минутах) потребляемых услуг телефонной компании, y - объем потребления всех других благ, цена которых равна 1 ед.
20 Часть II.
2.2 Решения Решение Задачи № 1 Из графика видно, что с ростом дохода от нуля до некоторого уровня объем потребления товара возрастает, так что благо является нормальным; при дальнейшем росте дохода данный товар вытесняется некоторым заменителем, объем его потребления снижается и товар становится низшим.
– – –
Комментарии.
1. Знак производной всегда совпадает со знаком эластичности. Поэтому ответы на все вопросы задачи можно было получить, рассматривая диапазоны уровней дохода, в пределах которых значения EI[q] превышают единицу, лежат между нулем и единицей и оказываются отрицательными.
2. Современная классификация потребляемых благ берет начало с исследований Э. Энгеля, выполненных в середине XIX в. и, естественно, не использовавших понятия эластичности функций. Проанализировав структуру потребительских бюджетов, Энгель установил, что с ростом дохода сумма расходов на питание возрастает, но их доля в распределении дохода падает. Если мы рассматриваем определенный товар, потребляемый в количестве q и покупаемый по цене p (которую мы считаем здесь неизменной), то расходы равны pq.
Доля, приходящаяся на данный товар, равна pq/I; если она с ростом дохода убывает, то EI 0. Воспользовавшись свойствами эластичности (см. Приложение) и учитывая неизменность цены, представим это соотношение в виде EI[q] – 1 0, или EI[q] 1. При этом абсолютная сумма расходов возрастает, EI = EI[q] 0. Таким образом, закон Энгеля применительно к необходимому благу (подобно продуктам питания) формулируется в виде двойного неравенства 0 EI[q] 1.
22 Часть II.
– – –
от цены другого блага, а доля расходов на данное благо в величине дохода зависела только от параметров функции полезности и не зависела ни от дохода, ни от цен.
Постоянство доли расходов (независимость от дохода) означает, что оба блага занимают пограничное положение между необходимыми и роскошными благами. Независимость объема спроса на каждое благо от цены другого блага означает, что блага независимы в потреблении.
Доли расходов на каждое благо зависели не от абсолютных значений параметров и, а лишь от их соотношения.
Так, решение в п. а) не изменилось бы, если бы показатели степени равнялись не 3 и 2, а, скажем, 15 и 10 или 0.3 и
0.2. Последнее обстоятельство связано с тем, что функции полезности, связанные монотонно возрастающим преобразованием, представляют одну и ту же систему предпочтений (порядковая концепция полезности). Пусть x - вектор, представляющий набор благ, U1(x) и U2(x) - функции полезности, причем U2(x) = (U1(x)), где - монотонно возрастающая функция. В этом случае если U1(x1) U1(x2), то и U2(x1) U2(x2), т. е. набор, оцениваемый функцией U1 как более предпочтительный, так же оценивается и функцией U2. Возведение в положительную степень - монотонно возрастающее преобразование, и функция x15y10 = (x3y2)5 описывает ту же систему предпочтений, что и функция в задании a). Тот же результат дает и, например, логарифмирование:
U3(x) = 3 ln x + 2 ln y = ln(x3y2).
В заданиях потребитель ограничивался двумя благами, но выводы остаются справедливыми при произвольном числе благ. Пусть x = (x1, x2, …, xn) и n U (x) = xii, (1) i =1
– – –
Решение Задачи № 5 Нетрудно заметить, что U1(x, y) = ln U2(x, y). Логарифм - возрастающая функция. Если первый потребитель предпочитает набор (x1, y1) набору (x2, y2), т. е. если U1(x1, y1) U1(x2, y2), то U2(x1, y1) U2(x2, y2), а это означает, что второй потребитель также предпочитает первый набор второму. В рамках порядковой теории полезности предпочтения потребителей неразличимы.
Потребление и спрос. 27
– – –
Решение Задачи № 6 Одна из аксиом потребительских предпочтений - аксиома ненасыщаемости («больше лучше, чем меньше»). Поэтому представляется очевидным, что любой потребитель предпочтет продукт 2 продукту 1 (x2 x1 и y2 y1) - продукт 2 доминирует над продуктом 1. На рисунке область доминирования по отношению к продукту 1 («северо-восточный угол») показана штриховыми линиями; точка, соответствующая продукту 2, располагается в этой области. Если по отношению к данному продукту есть доминирующий (на графике он располагался бы правее и выше данного), то ни один потребитель не выберет данный продукт. Таким образом, продукт 1 не может быть продан.
Кроме того, продукт не может быть продан, если он уступает по обеим характеристикам некоторому набору продуктов, приобретаемому за ту же цену. Если в набор входят n продуктов в количествах i, таких что n
– – –
и если каждый из продуктов мог быть куплен за одну денежную единицу, то и набор может быть куплен также за одну единицу. Если некоторый продукт доминируется набором из других продуктов, то каждый потребитель предпочтет ему этот набор.
Если выбор осуществляется в пространстве двух характеристик, достаточно ограничиться двухпродуктовыми наборами; все возможные наборы из двух конкретных продуктов графически представляются отрезками, соединяющими точки, обозначающие эти продукты. Таким образом, если на графике правее и выше данного продукта имеются точки отрезка, соединяющего два других продукта, то это означает, что существуют наборы, доминирующие над данным продуктом. Если составить набор из третьего и пятого продуктов в количествах 3 =, 5 =, то мы получим набор с характеристиками x = 6 = x4 и y = 6 y4 (точка 4 на рисунке), доминирующий по отношению к четвертому продукту (для доминирования i над j требуется xi xj и yi yj, причем по крайней мере одно из неравенств должно быть строгим).
30 Часть II.
Решение Задачи № 7
– – –
жается при росте цены этого блага, но возрастает с увеличением цены другого блага. Это означает, что блага являются взаимно заменяющими.
Решение Задачи № 9
– – –
нарушении этого условия домашнее хозяйство полностью отказывается от блага Y, так что y = 0. Но в таком случае и выражение для x становится неверным: так как весь доход расходуется на благо X, объем его потребления равен x = I/pX.
Для проверки этого предположения выясним, какие значения принимает предельная норма замены на бюджетной границе, описываемой равенством pXx + pYy = I. Из условия y 0 следует, что pXx I и x I /pX. Поэтому на бюджетной границе p2 162 MRS XY = 2 X = 2.
I2 x I Равенство MRSXY = pX /pY = 16/25 = 0.625 есть условие внутреннего потребительского оптимума. При I = 70 предельная норма замены на бюджетной границе не меньше 162/702 0.052, и в некоторой точке (а именно x = 1.25, y = = 2) она равна 0.625. Это и есть найденный выше внутренний оптимум. При I = 15 на бюджетной границе MRSXY 162/152 1.138 и значения, равного 0.625, на бюджетной линии не существует. Это означает, что потребительский оптимум занимает граничное, или, как его чаще называют в экономике, угловое положение. Таким образом, Комментарий.
Если при некоторых значениях (x, y), лежащих на бюджетной границе, имеет место неравенство MRSXY pX /pY, то в интересах потребителя несколько увеличить потребление блага X, соответственно сократив потребление блага Y. Если неравенство имеет противоположный знак, то потребитель может повысить полезность потребляемого набора, сместившись вдоль бюджетной границы в сторону уменьшения Потребление и спрос. 33 потребления блага X и увеличения потребления блага Y.
Если в некоторой внутренней точке бюджетной границы выполняется равенство MRSXY = pX / pY, то, как следует из выпуклости кривых безразличия к началу координат, и увеличение, и уменьшение значения x привели бы к снижению полезности. Это и означает, что в данной точке достигается потребительский оптимум. Но если на бюджетной границе всюду имеет место соотношение MRSXY pX/pY, то в каждой внутренней точке границы потребитель заинтересован в увеличении x, так что оптимум достигается при полном расходовании дохода на покупку блага X и отказе от блага Y.
Решение Задачи №10
– – –
объем потребления невозможен, полученный результат означает, что внутренний оптимум потребителя при данных условиях не существует. Следовательно, оптимум принимает граничное положение: x = 0, y = I/pY = 50. См. комментарий к предыдущей задаче.
Решение Задачи № 11
– – –
от дохода рассматривается в предположении фиксированных цен, для эластичности доли справедливо равенство EI[s] = EI = EI[x] – 1 (см. Приложение). Для возрастающей доли EI[s] 0, для убывающей доли EI[s] 0, откуда следуют оба утверждения.
Светуньков С.Г.
Точка пересечения кривой спроса с осью координат характеризует некоторый объем спроса, который зависит от дохода потребителя. Для того, чтобы изучить эту зависимость, мне придется использовать основные достижения теории мотивации.
Точка пересечения кривой спроса с осью объемов интересна тем, что цена товара при этом оказывается равной нулю. Таким образом, она характеризует тот объем товара, который согласен взять бесплатно покупатель при данном доходе - ведь единица товара при этом ничего не стоит! Естественно, что указанный объем характеризует способность покупателя при том доходе, который он имеет, транспортировать и хранить данный товар, а также его желание (и потребность) сделать это.
Значит, этот объем характеризует тот предел бесплатного пользования товаром, при переходе за который пользователь несет столь значительные неудобства, что он готов их нести только за вознаграждение (переход в отрицательную часть значений цены). Поэтому назову этот объем "граничным объемом потребления".
Как меняется этот граничный объем потребления в зависимости от дохода? С одной стороны, в русском языке такая ситуация получила емкое определение: "На халяву и уксус сладкий", и кажется, что этот предел не определен и устремляется в бесконечность при стремлении в бесконечность самого дохода. Однако, с другой стороны, очевидно, что мультимиллионер совершенно спокойно обойдется и без "халявного уксуса", предпочтя ему другие ценности - по крайней мере, он ограничится небольшим объемом уксуса, необходимого ему для рационального потребления. Человек с минимальным уровнем дохода при этом предложении готов взять столько "халявного уксуса", сколько он окажется в состоянии взять, транспортировать и разместить.
Таким образом, точка пересечения кривой спроса с осью объемов представляет собой достаточно сложную и нелинейную функцию зависимости граничных объемов спроса от дохода покупателя, которая требует дополнительного исследования. Оговорюсь сразу, что в данном случае мною рассматривается конечный потребитель - домохозяйство. Для этого потребителя характерны все человеческие ценности и мотивы поведения.
Если доход такого потребителя равен нулю, то и объема платежеспособного спроса как такового не существует. Впрочем, можно утверждать и другое - потребитель с нулевым доходом не имеет ни жилья, ни одежды, ни денег. Трудно себе представить, каким образом голый потребитель будет брать предлагаемый бесплатно товар. Поэтому утверждение о том, что при нулевом доходе будут нулевые покупки, мне представляется очень логичным и обоснованным.
При появлении минимальной величины дохода покупатель оказывается в состоянии более активно вступать в товарно-денежные отношения. При этом стремления покупателя взять необходимый товар бесплатно велики и ограничиваются только способностью покупателя это сделать - возможностью унести товар и где-то его хранить.
Чем выше становится доход у покупателя, тем в большем размере у покупателя появляется возможность взять товар впрок - он может уже использовать для переноса товара в зависимости от собственных доходов сетку, сумку, тележку, велосипед, автомобиль и т.п.
Хранить товар в этом случае в зависимости от собственных доходов (и соответственно от особенностей своего имущества) он может: в помещении на полу, в ящике, на полке, в шкафу, в комнате, в гараже и т.д. Значит, точка 1 имеет тенденцию к увеличению с увеличением дохода у потребителя.
В то же время доход характеризует степень богатства индивидуума, его способность удовлетворять все возрастающие потребности в разнообразных товарах, а значит, и его желание и способность терпеть или не терпеть те или иные неудобства. Трудно себе представить, что достаточно богатый человек предпочтет жить в прекрасном доме с великолепной мебелью, которая полностью забита впрок бесплатным сыром и с проходами между мебелью, загороженными коробками с этим товаром. Для богатого потребителя с очень большим доходом проще потратить деньги на приобретение и немедленное потребление небольшого объема товара, чем терпеть неудобства с его хранением впрок, хотя от некоторой части бесплатного товара он вряд ли откажется.
Таким образом, при незначительных доходах потребителя объемы потребления бесплатного товара ограничиваются способностью к сохранению этого товара потребителем, и этот участок функции может характеризоваться нелинейной возрастающей зависимостью граничного объема от дохода, причем вторая производная этой зависимости положительна.
При последующем увеличении дохода потребителя, несмотря на то, что способности к транспортировке и хранению бесплатного товара увеличиваются, потребитель перестает наращивать объемы потребления в такой же степени, как и при низких доходах - причиняемые при этом неудобства начинают уменьшать полезность больших объемов бесплатного продукта. В этой части зависимости она также имеет нелинейный характер, причем ее вторая производная становится отрицательной - интересы потребителя "переключаются" на удовлетворение других по иерархии потребностей.
При достижении определенного уровня дохода его дальнейшее увеличение не приводит к увеличению граничного объема потребления - интерес потребителя к данному товару не увеличивается. Бесплатного товара хватает с избытком, и потребитель начинает понимать, что такой объем бесплатного товара становится ему в тягость. Наступает насыщение - потребляется максимальный объем товара. Обозначу этот максимальный объем через Qmax. Это означает, что при достижении этого предела точка 1 перестает двигаться вдоль оси объемов в сторону увеличения с ростом дохода потребителя.
Что происходит, если доходы потребителя увеличиваются дальше? Потребности потребителя в данном товаре удовлетворены полностью и с большим запасом, а его все возрастающий доход начинает ориентировать его на новый товар или, по крайней мере, дает ему гарантию, что при появлении у данного, пока еще бесплатного товара, некоторой ненулевой цены, он без особых проблем сможет удовлетворить свою потребность в нем - доходы потребителя позволяют ему быть уверенным в этом. Большие запасы товара становятся потребителю в тягость, тем более, что появляется возможность удовлетворения потребностей более высокого уровня или, в предельном случае, получения бесплатно более интересного покупателю товара. Тогда объемы потребляемого бесплатно товара начинают уменьшаться. Сначала они уменьшаются постепенно, с ростом дохода (жаль ведь не брать бесплатный товар!), а затем - во все убывающих масштабах.
Таким образом, при достижении некоторого значения дохода Сtr происходит "переключение" интереса покупателя на новый товар и объемы бесплатного потребления данного товара начнут уменьшаться при доходе, который становится больше данного Сtr. Предел этого уменьшения может быть различным - это определяется характером товара, тем, является ли он предметом повседневного спроса или нет.
Так, если товар имеет альтернативу (например, ламповый радиоприемник имел альтернативу в виде транзисторного приемника), то объемы потребления этого товара падают до нуля - происходит полное переключение спроса на альтернативный товар с подобными же потребительскими свойствами.
Если же товар не имеет альтернативы, по крайней мере, в обозримой перспективе, например, картофель для большинства россиян, то объемы его потребления при дальнейшем увеличении дохода потребителя уменьшаются до некоторой степени и стабилизируются около отметки, которую следует назвать рациональной нормой потребления Qrat.
Естественно, что описанное выше поведение характерно для среднего потребителя, а не для каждого в отдельности. Вкусы каждого потребителя очень своеобразны - мы знаем, что порой достаточно обеспеченные люди обладают удивительными наклонностями к потреблению совершенно нехарактерных объемов продуктов для этого уровня обеспеченности. Так, я был хорошо знаком с одним российским доктором наук, который, достаточно прилично зарабатывая, тем не менее занимался активным огородничеством и за сезон выращивал и собирал на своем загородном участке пятьдесят мешков картофеля (две с половиной тонны). Как видно, в этом случае объемы потребления картофеля его семьей совершенно не соответствуют ее доходам и выбивается из приведенной закономерности.
Указанный пример еще раз подчеркивает то обстоятельство, что я рассматриваю поведение некоторого усредненного потребителя. Понятно, что если мы соберем статистические данные по всем докторам наук в современной России, то объем потребления картофеля семьей среднестатистического доктора наук будет значительно меньше двух с половиной тонн в год. Именно для такого характерного потребителя с увеличением его доходов граничные объемы потребления картофеля после достижения потребителем определенного уровня дохода начинают уменьшаться.
На графике рисунка 1 изображена схематически описанная выше нелинейная зависимость граничного объема потребления Q на некоторый товар от величины дохода С покупателя при нулевой цене на этот товар. На графике каждая точка, лежащая на кривой граничного объема, соответствует точкам, подобным точке 1 графика кривых спроса рисунка 3, то есть лежащим на оси ординат, для которых абсцисса (цена) является величиной постоянной и равной нулю.
Приведенные выше соображения, как уже говорилось, являются весьма абстрактными - трудно представить себе, чтобы какой-либо товар раздавался бесплатно, да еще в неограниченных количествах.
Рисунок 1. Кривая зависимости граничного объема потребления Q от величины дохода С
Поэтому все приведенные выше соображения могут показаться придирчивому читателю недостаточно обоснованными и лишенными какого-либо экономического смысла. Этот недостаток вполне может быть устранен. Обоснованными покажутся такому читателю подобные же рассуждения, если их провести при условии задания некоторой фиксированной, достаточно малой цены, не равной нулю. Но на самом деле и эта процедура легко может быть формализована в той же графической постановке, которая была только что использована. При этом будет получена та же самая зависимость.

Рисунок 2. Исходный график кривых спроса и предложения при условии задания фиксированной цены P0
Действительно, графически на плоскости объем-цена переход к ненулевым ценам означает перенос оси ординат (объема) вправо на величину, равную некоторой фиксированной цене P0. Эта процедура изображена на графике рисунка 2, где изображены кривые спроса. Точка 1 при этом перемещении оси ординат передвигается вправо вниз и обозначается на рисунке через 1". Рассуждения, приведенные выше для случая бесплатного товара, полностью подтвердятся и в этом случае. Изменятся лишь некоторые пропорции. Например, как это со всей очевидностью следует из рисунка 2, для каждой величины дохода объемы потребления товара уменьшатся по сравнению с вариантом его бесплатной раздачи.
Принципиальным отличием поведения объема потребления товара при фиксированной ненулевой цене в зависимости от поведения граничного объема потребления товара при нулевой цене заключается в том, что для некоторых товаров, не являющихся предметами повседневного спроса, зависимость объема потребления от дохода потребителя начинается не из точки начала координат (рисунок 3).
Действительно, если рассматриваемый товар не является товаром повседневного спроса, то он приобретается только после того, как будут удовлетворены потребности повседневного спроса и у покупателя появляется возможность реализовать при увеличении собственного дохода потребность в данном товаре. Поэтому кривая зависимости объема потребления товара от дохода потребителя в данном случае будет исходить из точки, для координат которой характерно следующее:
Доход потребителя положителен и не ниже фиксированной цены товара (Cmin > P0),
Объем приобретаемого товара равен нулю (Q0 = 0).

Рисунок 3. Кривая зависимости объема потребления Q от величины дохода С при цене товара, не равной нулю
Из графиков рисунков 1 и 3, которые изображают один тип и характер зависимости, следует ряд вполне очевидных вопросов на которые следует найти ответы:
Насколько два указанные графика похожи друг на друга и каковы их принципиальные отличия, как они взаимосвязаны;
Как поведет себя кривая зависимости объема потребления Q от величины дохода С при дальнейшем увеличении цены;
Как поведет себя величина максимального объема потребления Qmax и объем рационального потребления Qrat при увеличении цены на товар?
Возможны различные варианты ответов на поставленные вопросы в зависимости от того, какой товар предложен покупателю. Есть утверждения вполне очевидные, не требующие каких-либо особых доказательств. С увеличением цены на товар сама кривая, очевидно, будет сдвигаться вправо - нужны все большие доходы для того, чтобы приобрести данный объем товара по повышенной цене.
Что касается рациональной нормы потребления Qrat, то и здесь все достаточно очевидно. Эта величина не будет меняться, так как она характеризует отнюдь не покупательскую способность, а рациональные потребности, когда доход покупателя так велик, что он может не обращать особого внимания на цену данного товара, она с позиций его доходов почти равна нулю.
Сама кривая с увеличением цены товара, как уже говорилось, будет сдвигаться вправо. Этот сдвиг может являться параллельным, а может и не быть таковым.
Первый случай достаточно прост (рисунок 4) и, по-видимому, характеризует тот товар, который называют "предметом повседневного спроса". Для такого товара сложно предполагать что-либо другое - все характерные ординаты кривой остаются неизменными.

Рисунок 4. Движение кривой зависимости объема потребления Q от величины дохода С при увеличении цены товара повседневного спроса
Так, например, максимальный объем потребления, который характеризует некоторое ажиотажное потребление, также остается неизменным. Действительно, этот объем вполне определяется двумя факторами - данной ценой товара и доходом Сtr при котором происходит "переключение" интереса покупателя на новый товар. С увеличением цены на товар этот доход, характеризующий "переключение", также увеличивается на величину этого товара.
Но если товар не является предметом повседневного спроса (рисунок 5), то его цена начинает влиять на поведение потребителя. Так, например, если мне предложить бесплатно гаванские сигары лучших сортов, то я, человек не курящий, наверняка все же возьму их некоторое количество - угостить своих курящих друзей или для целей получения водяного настоя, уничтожающего садовых вредителей на даче.
Если же этот товар будет предложен мне за деньги, то при небольшой цене этих сигар, я, пожалуй, все-таки приобрету их некоторое количество, но уже в меньшем объеме.
Если цену на сигары повысить еще больше, то я ни при каких собственных доходах, какими бы высокими они ни были, их не приобрету - у меня есть куда потратить деньги, есть интересы и потребности, которые следует удовлетворить.
Подобное поведение, как я смею думать, вовсе не является особенностью моего характера. Аналогично поступит подавляющее большинство нормальных людей.
Графически такое поведение означает, что с ростом цены на товар максимальный объем его потребления будет уменьшаться (рисунок 5). Также будут меняться и некоторые пропорции самой кривой.

Рисунок 5. Движение кривой зависимости объема потребления Q от величины дохода С при увеличении цены товара, не являющимся предметом первой необходимости
При увеличении цены до определенного предела, кривая превратится в точку, лежащую на оси абсцисс. Таким образом, возможны два типа кривых зависимости объема потребления от дохода потребителя при изменяющейся цене - для товара повседневного спроса и для товара, таковым не являющимся. Это обстоятельство следует рассмотреть более подробно, и я в последующих параграфах работы остановлюсь именно на этих двух товарах. С сожалением могу констатировать, что четкого определения понятия <товар повседневного спроса> в научной литературе я не встречал. По-видимому, предполагается, что оно аксиоматично. Это досадное обстоятельство во многом помешает получить конкретные рекомендации в последних частях книги. Пока что приходится разделять товар на эти две группы, только основываясь на собственных представлениях о товаре.
МЕТОДИЧЕСКИЕ ПОЯСНЕНИЯ
Ниже приведены примеры решения типовых задач и упражнений
Тема 1. Система макроэкономических взаимосвязей
Задача 26 . На основании данных, приведенных в таблице, определите:
1) ВНП по доходам;
2) ВНП по расходам;
5) национальный доход.
Решение
1 Определяем ВНП по доходам. Он включает амортизацию, косвенные налоги на бизнес, заработную плату наемных работников, дивиденды, процент, доходы от индивидуальных вложений, арендную плату, нераспределенные прибыли, налоги на прибыль корпораций, арендную плату:
ВНП по доходам = 1 010 + 786 + 5 810 + 196 + 290 + 158 + 40 + 650 + 784 = 9 724 млн. долл.
2 Определяем ВНП по расходам:
ВНП по расходам = C + Ig + Xn + G,
где C – личные потребительские расходы;
Ig – валовые внутренние частные инвестиции;
G – государственные закупки товаров и услуг;
Xn – чистый экспорт.
ВНП по расходам = 6 452 + 1 530 – 186 + 1 928 = 9 724 млн. долл.
ВНП по расходам должен быть равен ВНП по доходам.
3 Определим ВВП:
ВВП = ВНП – Хn = 9 724 + 186 = 9 910 млн. долл.
4 Определим ЧНП:
ЧНП = ВВП – А = 9 910 – 1 010 = 8 900 млн. долл.
где А – амортизация.
5 Определим национальный доход:
НД = ЧНП – косвенные налоги на бизнес,
НД = 8 900 – 786 = 8 114 млн. долл.
Задача 27. ВНП равен 9 000 ден. ед., потребительские расходы – 5 200 ден. ед., государственные расходы – 1 900 ден. ед., а чистый экспорт – 180 ден. ед. Рассчитайте:
1) величину валовых инвестиций;
2) ЧНП, если сумма амортизации равна 850 ден. ед.;
Если в этом примере чистый экспорт выражается положительной величиной, может ли она быть отрицательной. В каком случае?
Решение
1 ВНП по рас = С + Ig + G + Xn ,
где С - потребительские расходы;
Ig - валовые инвестиции;
G - государственные расходы;
Xn - чистый экспорт.
Ig = ВНП – С – G – Xn,
Ig = 9000 – 5200 – 1900 – 180 = 1820;
2 ЧНП = ВНП – А,
ЧНП = 9000 – 850 = 8150.
3 Если импорт будет больше экспорта.
Тема 2. Потребление, сбережение, инвестиции
Задача 14. Экономика характеризуется следующими данными:
а) функция потребления С = Са + MPC· Y;
б) автономные инвестиции Ia единиц;
в) государственные закупки G единиц;
г) предельная ставка налогообложения t;
д) трансфертные платежи TR.
Существующие производственные мощности позволяют увеличить национальный доход в 1,25 раза. Как государство должно изменить свои закупки, чтобы обеспечить полное использование производственных мощностей при сбалансированности государственного бюджета? Каким может быть изменение трансфертных платежей?
Решение
Определим равновесный уровень доходов:
m =1/(1– mpc (1– t)) = 1/(1 – 0,55· (1 – 0,1)) = 1,98;
A = Ca + G + Ia +TR· mpc,
A = 50 + 100 + 400 + 200 · 0,55 = 660;
Y = 1,98 · 660 = 1 306,8.
Определим изменение равновесного объема производства:
Y2 = 1,25 · 1 306,8 = 1 633,5.
Определим, на сколько должны измениться государственные закупки:
DY = 1 633,5 – 1 306,8 = 326,7;
DG = 326,7/1,98 = 165.
Определим, на какую величину должны измениться трансфертные платежи:
DTR · mpc = 165;
DTR = 165/0,55 = 300.
Задача 16. Если функция сбережений описывается формулой S = –30+0,1Y, а автономные инвестиции составляют величину 125, то каков будет равновесный уровень национального дохода?
Решение
При равновесном уровне национального дохода величина автономных инвестиций равна сбережению.
Тогда I = S ,
125 = – 30 + 0,1 у,
Y равн = 1 550.
Ответ : равновесный уровень национального дохода 1 550.
Задача 17 . Функция потребления задана формулой С = 100 + 0,2 Y.
1) постройте график потребления;
2) постройте график сбережения;
3) определите равновесный объем национального дохода;
4) определите величину мультипликатора расходов при условии, что доход составляет 0; 200; 400; 600; 800.
Решение
Построим таблицу:
1 По данным таблицы строим график потребления:
Рассчитаем равновесный доход аналитически.
Приравняем Y = С, тогда Y = 100 + 0,2Y.
2 По данным таблицы строим график сбережения:
 |
Предельная склонность к сбережению равна:
MPS = 1 – MPC = 1– 0,2 = 0,8.
Тогда величина мультипликатора μ равна:
 .
.
Объем потребления некоторого товара домашним хозяйством (q) в зависимости от дохода (I) описьпвается равенством:
Определить, при каких значениях дохода товар для данного домашнего хозяйства является
а) низшим благом;
б) нормальным благом;
в) необходимьм благом;
г) роскошным благом.
ЗАДАЧА № 2
Индивид потребляет два блага в количествах x и y соответственно. Согласуются ли приведенные ниже функции полезности с аксиомами потребительских предпочтений? (да/нет)
а) U(x, y) = yjx2 + y2 ;
в) U(x, y) = - +
ЗАДАЧА № 3
Предпочтения индивида характеризуются предельными нормами замещения MRSxy = 2, MRSxz = 0.8. Найти предельные нормы замещения а) MRS , б) MRS , в) MRS , г) MRS .
А 1 / yx7 / zx7 " yz7 " zy
ЗАДАЧА № 4
Домашнее хозяйство потребляет два блага в количествах x и y; его предпочтения описываются функцией полезности U(x, y). Найти функцию спроса домашнего хозяйства, если
а) U(x, y) = x3y2;
б) U(x, y) = xaye.
ЗАДАЧА № 5
Предпочтения двух индивидов описываются функциями полезности
U-(x, y) = --; U2(x, y) = ln x + ln y ln(x + y).
Различаются ли предпочтения этих индивидов? ЗАДАЧА № 6
Рассмотрим модель, в которой предпочтения потребителя относятся не к продуктам, а к характеристикам, которыми продукты обладают (модель Ланкастера). Допустим, что рассматривается множество продуктов, обладающих двумя характеристиками (X и Y).
| Продукт (0 | ||
Обозначим (x., y) количественные меры соответствующих характеристик в единице і-го продукта, причем простоты ради в качестве единицы каждого продукта принимается количество продукта, приобретаемое за одну денежную единицу. Будем считать, что предпочтения в пространстве характеристик удовлетворяют тем же аксиомам, что и предпочтения в пространстве благ в традиционной теории.
В таблице (см. выше) приведены данные по шести различным продуктам. Какие из них не имеют перспектив быть проданными на рынке?
ЗАДАЧА № 7
Домашнее хозяйство потребляет два блага, X и Y, в количествах x и y; его доход I = 60, а предпочтения описываются функцией полезности U(x, y) = xy .
благ pX = 9, pY = 4.
из благ от цен и дохода.
ЗАДАЧА № 8
Домашнее хозяйство потребляет два блага, X и Y, в количествах x и y; его предпочтения описываются функцией
полезности U(x, y) = л/x + yfy . Известен доход: I = 60.
а) Найти объемы спроса на каждое из благ при ценах
благ pX = 10, pY = 5.
б) Определить зависимости объемов спроса на каждое
из благ от цен и дохода.
в) Определить характер взаимозависимости благ в потреблении.
ЗАДАЧА № 9
Домашнее хозяйство потребляет два блага, X и Y, в количествах x и y; его предпочтения описываются функцией по1
лезности U(x, y) = y , цены благ равны pX = 16, pY = 25.
x X а) Найти объемы спроса на каждое из благ при значениях дохода I = 70; I = 15.
б) Определить зависимости от дохода объемов спроса на каждое из благ.
ЗАДАЧА № 10
Индивид потребляет два блага, X и Y, в количествах x и y соответственно. Функция полезности индивида: U = ax + by + xy, a > 0, b > 0.
а) Пусть a = 10, b = 25. Определить объемы потребления благ,
если цены благ pX = 5, pY = 2 при доходе индивида I = 200;
б) то же при доходе индивида I = 100;
в) при каких соотношениях дохода и цен оптимум потребителя будет внутренним (x > 0, y > 0)?
ЗАДАЧА № 11
Домашнее хозяйство приобретает благо X, производимое естественной монополией, по цене pX = 10 в количестве x = = 5. Государство, регулирующее цену продукта естественной монополии, сочло целесообразным повысить цену до p"X = = 14 и выплачивать домашнему хозяйству компенсацию в размере (p"X pX) x = 20.
а) Изменилось ли благосостояние домашнего хозяйства,
и если да, то в какую сторону?
б) Проверить утверждение на следующем примере: домашнее хозяйство кроме блага X потребляет еще одно благо, Y, цена которого pY = 1 не изменилась; доход домашнего
хозяйства I = 100, а функция полезности U(x, y) = -Jxy .
ЗАДАЧА № 12
Классификация благ, основанная на кривых Энгеля, учитывает изменения доли дохода, направленной на покупку рассматриваемого блага, в зависимости от изменения дохода. Докажите следующие утверждения:
если доля дохода, направляемая на покупку данного блага, увеличивается с ростом дохода, то эластичность объема потребления по доходу больше единицы;
если доля дохода, направляемая на покупку данного блага, уменьшается с ростом дохода, то эластичность объема потребления по доходу меньше единицы.
ЗАДАЧА № 13
Домашнее хозяйство потребляет три блага, X, Y и Z. Их доли в расходах составляют соответственно sX = 50\%, sY = = 30\%, sZ = 20\%. Известны эластичности по доходу объемов потребления благ X и Y: EI[x] = 2, E^y] = 0.6.
а) Найти эластичность объема потребления блага Z по
б) Определить, к какому типу относится каждое из благ.
ЗАДАЧА № 14
Докажите утверждение: если среди благ, потребляемых домашним хозяйством, есть хотя бы одно низшее, то среди них имеется также хотя бы одно роскошное.
ЗАДАЧА № 15
Телефонная компания предлагает потребителям услуг на выбор два варианта тарифов: (а) 4 ед./мин без абонентской платы; (б) 2 ед./мин и абонентская плата 20 ед. Какой из тарифов выберет каждый из следующих потребителей:
функция полезности U1 = x0.5y0.5, доход 11 = 100 ед.;
функция полезности U2 = x0.25y0.75, доход 12 = 100 ед.;
функция полезности U3 = x0.25y0.75, доход I = 200 ед. Здесь x - количество (в минутах) потребляемых услуг
телефонной компании, y - объем потребления всех других благ, цена которых равна 1 ед.
2.2 РЕШЕНИЯ
РЕШЕНИЕ ЗАДАЧИ № 1
Из графика видно, что с ростом дохода от нуля до некоторого уровня объем потребления товара возрастает, так что благо является нормальным; при дальнейшем росте дохода данный товар вытесняется некоторым заменителем, объем его потребления снижается и товар становится низшим.
Найдем границы области возрастания объема потребления;
для этого продифференцируем объем потребления по доходу:
dq = _ 2I (I +10)8 8I2(I +10)2 = _ 20I -12
dI (I +10)6 (I +10)4.
Производная обращается в нуль при I = 20; при меньших значениях дохода производная положительна, и объем возрастает, при больших - убывает. Таким образом, товар является нормальным при I < 20 и низшим - при I > 20.
Для того чтобы выяснить, при каких уровнях дохода товар является необходимым благом, а при каких - роскошным, целесообразно воспользоваться эластичностью объема потребления по доходу: 1 q dl I +10
Для роскошного блага эластичность объема потребления по доходу больше единицы. Последнее равенство показывает, что EI[q] > 1 при 0 < I < 5. Если 5 < I < 20, то потребление растет с доходом, но медленнее, чем доход, BI[q] < 1, и рассматриваемый товар является необходимым благом.
Итак, рассматриваемый товар является низшим благом при I > 20 и нормальным - при I < 20; при 0 < I < 5 он является роскошным благом, при 5 < I < 20 - необходимым.
Комментарии.
Знак производной всегда совпадает со знаком эластичности. Поэтому ответы на все вопросы задачи можно было получить, рассматривая диапазоны уровней дохода, в пределах которых значения BI[q] превышают единицу, лежат между нулем и единицей и оказываются отрицательными.
Современная классификация потребляемых благ берет начало с исследований Э. Энгеля, выполненных в середине XIX в. и, естественно, не использовавших понятия эластичности функций. Проанализировав структуру потребительских бюджетов, Энгель установил, что с ростом дохода сумма расходов на питание возрастает, но их доля в распределении дохода падает. Если мы рассматриваем определенный товар, потребляемый в количестве q и покупаемый по цене p (которую мы считаем здесь неизменной), то расходы равны pq. Доля, приходящаяся на данный товар, равна pq/I; если она с ростом дохода убывает, то BI < 0. Воспользовавшись свойствами эластичности (см. Приложение) и учитывая неизменность цены, представим это соотношение в виде BI[q] 1 < 0, или BI[q] < 1. При этом абсолютная сумма расходов возрастает, EI = BI[q] > 0. Таким образом, закон Энгеля применительно к необходимому благу (подобно продуктам питания) формулируется в виде двойного неравенства 0 < EI[q] < 1.
РЕШЕНИЕ ЗАДАЧИ № 2
Аксиомы потребительских предпочтений:
полнота (сопоставимость любых потребительских наборов);
транзитивность;
ненасыщаемость («больше - лучше, чем меньше», предпочтительность набора, содержащего больший объем любого блага без уменьшения объемов остальных);
непрерывность;
выпуклость множества наборов, предпочтительных по отношению к любому данному.
Если система предпочтений потребителя задана функцией полезности, то аксиомы 1 и 2 тем самым выполняются. Аксиома 4 выполняется, если функция полезности непрерывна. Во всех вариантах а) - в) функции полезности непрерывны, так что требования аксиом 1, 2 и 4 можно считать выполненными.
Аксиома 3 выполняется, если функция полезности возрастает по каждому аргументу. Функция варианта а), очевидно, удовлетворяет этому требованию, варианта в) - нет, она является убывающей по каждому аргументу. Так как
т. е. значения функций б) и в) - взаимно обратные величины, функция б) является возрастающей (в чем можно убедиться и любым иным способом).
Аксиома 5 требует, чтобы каждая кривая безразличия
ограничивала снизу выпуклую область. Это означает, что
предельная норма замены MRS должна убывать с ростом
x и возрастать с ростом y. Функция а) этому требованию не
отвечает: соответствующие кривые безразличия - 90-градусные дуги окружностей с центром в начале координат.
Для функции б) ^ ^2 ґ 2
dU / dx = -2- I ; dU / dy =
так что 2 MRS ==Udx = (У1 .
Таким образом, функция б) удовлетворяет всем аксиомам предпочтений. Ответ:
а) нет; б) да; в) нет. РЕШЕНИЕ ЗАДАЧИ № 3
Если единица блага x замещается a единицами блага y с сохранением уровня полезности, то единица блага y замещается 1/a единицами блага x. Поэтому MRS = 1/MRS .
Если к тому же единица блага y замещается b единицами блага z при том же условии, то единица блага x замещается ab единицами блага z и поэтому
MRS MRS = MRS .
Это позволяет найти все неизвестные предельные нормы замещения по известным MRS и MRS .
Комментарий.
Более формализованный подход связывает предельные нормы замены с производными функции полезности:
MRS = Udx и т. п.,
откуда следуют приведенные выше соотношения. Заметим, что система предпочтений определяет функцию полезности неоднозначно: если функция U(x, y, ...) описывает предпочтения данного потребителя, то точно так же их описывает функция U1(x, y, ...) = cp(U(x, y, ...)), где ф - произвольная монотонно возрастающая функция. Но
dU1 / dx = (dp / dU) ■ (dU / dx) = dU / dx
dU1/dy ~ dp / dU) ■ (dU / dy) " dU / dy " так что отношение частных производных зависит не от количественной шкалы, в которой отображаются полезности, а лишь от предпочтений индивида.
а) 0.5; б) 1.25; в) 0.4; г) 2.5.
РЕШЕНИЕ ЗАДАЧИ № 4
а) Прежде всего, определим предельную норму замены
как функцию x и у:
U = 3x2y2; U = 2x3y, отсюда MRS = Ux = 3у.
При ценах благ p , p в точке оптимума потребителя соотношение цен p/p равно предельной норме замены, так что
Заметим, что p x и p у - это расходы потребителя соответственно на первое и второе блага. Отсюда ясно, как данный потребитель распределяет свой бюджет: долю 0.6 своего дохода он должен потратить на покупку первого блага, долю 0.4 - на покупку второго. Если его доход равен I, то объемы спроса на первое и на второе благо равны:
x = 0.6 -; у = 0.4 -.
Каждое из приведенных равенств описывает функцию спроса на соответствующее благо.
б) Те же рассуждения применительно к более общему
случаю приводят к соотношению:
откуда: РуУ Р
а + р px а+р py
Комментарий.
В приведенных задачах объем спроса на каждое благо зависел от дохода и от цены данного блага и не зависел
от цены другого блага, а доля расходов на данное благо в величине дохода зависела только от параметров функции полезности и не зависела ни от дохода, ни от цен.
Постоянство доли расходов (независимость от дохода) означает, что оба блага занимают пограничное положение между необходимыми и роскошными благами. Независимость объема спроса на каждое благо от цены другого блага означает, что блага независимы в потреблении.
Доли расходов на каждое благо зависели не от абсолютных значений параметров а и р, а лишь от их соотношения. Так, решение в п. а) не изменилось бы, если бы показатели степени равнялись не 3 и 2, а, скажем, 15 и 10 или 0.3 и 0.2. Последнее обстоятельство связано с тем, что функции полезности, связанные монотонно возрастающим преобразованием, представляют одну и ту же систему предпочтений (порядковая концепция полезности). Пусть x - вектор, представляющий набор благ, U^x) и U2(x) - функции полезности, причем U2(x) = ф(^1(х)), где ф - монотонно возрастающая функция. В этом случае если ^1(x1) > U^x2), то и U2(x^ > > U2(x2), т. е. набор, оцениваемый функцией U как более предпочтительный, так же оценивается и функцией U2. Возведение в положительную степень - монотонно возрастающее преобразование, и функция х15у10 = (х3у2)5 описывает ту же систему предпочтений, что и функция в задании a). Тот же результат дает и, например, логарифмирование:
U3(x) = 3 ln х + 2 ln y = 1п(х3у2).
В заданиях потребитель ограничивался двумя благами, но выводы остаются справедливыми при произвольном числе благ. Пусть x = (х1, х2, хп) и
Будем использовать обозначения для предельных по-лезностей,
Отсюда получаем выражение для предельных норм замены:
U. a. х. MRS.. = = , U. а.} х.
Полученное выражение позволяет при заданных ценах выразить расходы на все потребляемые блага через расходы на какое-нибудь одно, например первое:
MRS;/ = P = - Х, откуда:
р х\% = -рл. (3)
Теперь бюджетное ограничение можно представить в виде
так что с учетом равенства (2) p1x1 = a17, а равенство (3) показывает, что аналогичные выражения справедливы для всех благ: p.x. = aI. Таким образом, если функция полезности имеет вид (1), то доли расходов на отдельные блага в общей сумме не зависят ни от величины дохода, ни от цен. Они представляют собой постоянные величины, пропорциональные параметрам ai, а если эти параметры нормированы в соответствии с равенством (2), то доли совпадают с параметрами. Объем спроса на каждое благо равен х. = a.I/p..
РЕШЕНИЕ ЗАДАЧИ № 5
Нетрудно заметить, что U1(x, y) = In U2(x, y). Логарифм - возрастающая функция. Если первый потребитель предпочитает набор (х1, y1) набору (х2, y2), т. е. если U1(x1, y1) > U1(x2, y2), то U2(x1, y1) > U2(x2, y2), а это означает, что второй потребитель также предпочитает первый набор второму. В рамках порядковой теории полезности предпочтения потребителей неразличимы.
Комментарии.
По формульной записи функций полезности далеко не всегда легко догадаться, что одна из них является функцией от другой. Но это всегда можно выяснить, сравнив предельные нормы замены: если предельные нормы замены совпадают при любых комбинациях благ, то они выражают одну и ту же систему предпочтений индивидов. При решении задачи 2 определена предельная норма замены для первого индивида:
MRS1^ (x, y) = [Уj .
Для второго индивида
dU2 = 1 1 y dU2 = 1 1 x
dx x x + y x(x + y) dy y x + y y(x + y) так что
MRSxy (x, y) = dU/dx = {yT. xyK У" dU2/ dy ^ x J
Таким образом, для любых комбинаций (x, y) предельные нормы замены для обоих индивидов совпадают, следовательно, совпадают и их предпочтения.
Концепция порядковой полезности служит основой теории потребительского выбора при отсутствии риска. Для теоретического описания потребительского поведения в рисковой ситуации она оказывается недостаточной. В теории выбора в условиях риска утверждается существование такой функции полезности, к максимизации математического ожидания которой стремится потребитель (функция полезности фон Неймана-Моргенштерна). В этом отношении предпочтения индивидов в данной задаче различны, если условиями заданы функции полезности фон Неймана-Моргенштерна. Допустим, что в рассматриваемых примерах цены продуктов численно равны, так что, как легко проверить, в выбираемых обоими потребителями наборах x = y. Допустим также, что потребителю предлагают указать набор благ, столь же полезный, как лотерея из наборов (1, 1) и (5, 5) с равными вероятностями. Так как x x/(x + x) = x/2, первый потребитель укажет набор (x, x), удовлетворяющий условию:
0.5 .1 + 0.5 . 5 = x,
откуда x = 3, так что он укажет набор (3, 3). Соответствующее условие для второго потребителя:
0.5 . ln1 + 0.5 . ln5 = lnx,
откуда x = \ PxPy" Py +4 PxPy
в) Последние равенства показьпвают, что при фиксированной величине дохода объем спроса на каждое благо снижается
как при росте цены этого, так и при росте цены другого блага.
Это означает, что блага являются взаимно дополняющими.
РЕШЕНИЕ ЗАДАЧИ № 8
а, б) Рассуждая по аналогии с решением предыдущей задачи, находим:
MRSxy =л \% = ^ =
Отсюда y = x (p /pY)2 = 4x. Из равенства дохода и расходов, 10x + 5 4x = 60, находим x = 2, y = 8.
Зависимость объемов спроса от цен и дохода описывается равенствами
px ■ (1 + px / py) py ■ (1 + py / px)
в) Последние равенства показывают, что при фиксированной величине дохода объем спроса на каждое благо сни
жается при росте цены этого блага, но возрастает с увеличением цены другого блага. Это означает, что блага являются взаимно заменяющими.
РЕШЕНИЕ ЗАДАЧИ № 9
Найдем выражения для предельных полезностей: dU = J__ dU_ = 1
Так как в точке потребительского оптимума предельная норма замены равна соотношению цен, справедливо равенство
откуда непосредственно находится объем потребления блага X: x = Е = Ё5 = 1.25
Спрос на благо X, как мы видим, не зависит от дохода (в дальнейшем нам придется уточнить это утверждение). Спрос на Y явным образом от дохода зависит. При I = 70 имеем:
70 -у/16 25 „
Ясно, что объем потребления не может быть отрицательным. Но, согласно полученному выражению для у, условие у > 0 выполняется при I > 4~РхРу = 20 и нарушается в противном случае. Естественно предположить, что при нарушении этого условия домашнее хозяйство полностью отказывается от блага Y, так что y = 0. Но в таком случае и выражение для x становится неверным: так как весь доход расходуется на благо X, объем его потребления равен x = I/PX.
Для проверки этого предположения выясним, какие значения принимает предельная норма замены на бюджетной границе, описываемой равенством pXx + pYy = I. Из условия y > 0 следует, что pXx < I и x < I /pX. Поэтому на бюджетной границе
MRSxy = x > Т2" 7^Равенство MRSxy = pX /pY = 16/25 = 0.625 есть условие внутреннего потребительского оптимума. При I = 70 предельная норма замены на бюджетной границе не меньше 162/702 ~ 0.052, и в некоторой точке (а именно x = 1.25, y = = 2) она равна 0.625. Это и есть найденный выше внутренний оптимум. При I = 15 на бюджетной границе MRSxy > > 162/152 ~ 1.138 и значения, равного 0.625, на бюджетной линии не существует. Это означает, что потребительский оптимум занимает граничное, или, как его чаще называют в экономике, угловое положение. Таким образом,
У = при / > ^рхРу;