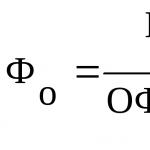Урок: как построить параболу или квадратичную функцию?
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Парабола — это график функции описанный формулой ax 2 +bx+c=0.
Чтобы построить параболу нужно следовать простому алгоритму действий:
1) Формула параболы y=ax 2 +bx+c
,
если а>0
то ветви параболы направленны вверх
,
а то ветви параболы направлены вниз
.
Свободный член c
эта точке пересекается параболы с осью OY;
2) , ее находят по формуле x=(-b)/2a , найденный x подставляем в уравнение параболы и находим y ;
3) Нули функции или по другому точки пересечения параболы с осью OX они еще называются корнями уравнения. Чтобы найти корни мы уравнение приравниваем к 0 ax 2 +bx+c=0 ;
Виды уравнений:
a) Полное квадратное уравнение имеет вид ax 2 +bx+c=0
и решается по дискриминанту;
b) Неполное квадратное уравнение вида ax 2 +bx=0.
Чтобы его решить нужно вынести х за скобки, потом каждый множитель приравнять к 0:
ax 2 +bx=0,
х(ax+b)=0,
х=0 и ax+b=0;
c)Неполное квадратное уравнение вида ax 2 +c=0.
Чтобы его решить нужно неизвестные перенести в одну сторону, а известные в другую. x =±√(c/a);
4) Найти несколько дополнительных точек для построения функции.
ПРАКТИЧЕСКАЯ ЧАСТЬ
И так теперь на примере разберем все по действиям:
Пример №1:
y=x 2 +4x+3
c=3 значит парабола пересекает OY в точке х=0 у=3. Ветви параболы смотрят вверх так как а=1 1>0.
a=1 b=4 c=3 x=(-b)/2a=(-4)/(2*1)=-2 y= (-2) 2 +4*(-2)+3=4-8+3=-1 вершина находится в точке (-2;-1)
Найдем корни уравнения x 2 +4x+3=0
По дискриминанту находим корни
a=1 b=4 c=3
D=b 2 -4ac=16-12=4
x=(-b±√(D))/2a
x 1 =(-4+2)/2=-1
x 2 =(-4-2)/2=-3
Возьмем несколько произвольных точек, которые находятся рядом с вершиной х=-2
х -4 -3 -1 0
у 3 0 0 3
Подставляем вместо х в уравнение y=x 2 +4x+3 значения
y=(-4) 2 +4*(-4)+3=16-16+3=3
y=(-3) 2 +4*(-3)+3=9-12+3=0
y=(-1) 2 +4*(-1)+3=1-4+3=0
y=(0) 2 +4*(0)+3=0-0+3=3
Видно по значениям функции,что парабола симметрична относительно прямой х=-2
Пример №2:
y=-x 2 +4x
c=0 значит парабола пересекает OY в точке х=0 у=0. Ветви параболы смотрят вниз так как а=-1 -1
Найдем корни уравнения -x 2 +4x=0
Неполное квадратное уравнение вида ax 2 +bx=0. Чтобы его решить нужно вынести х за скобки, потом каждый множитель приравнять к 0.
х(-x+4)=0, х=0 и x=4.
Возьмем несколько произвольных точек, которые находятся рядом с вершиной х=2
х 0 1 3 4
у 0 3 3 0
Подставляем вместо х в уравнение y=-x 2 +4x значения
y=0 2 +4*0=0
y=-(1) 2 +4*1=-1+4=3
y=-(3) 2 +4*3=-9+13=3
y=-(4) 2 +4*4=-16+16=0
Видно по значениям функции,что парабола симметрична относительно прямой х=2
Пример №3
y=x 2 -4
c=4 значит парабола пересекает OY в точке х=0 у=4. Ветви параболы смотрят вверх так как а=1 1>0.
a=1 b=0 c=-4 x=(-b)/2a=0/(2*(1))=0 y=(0) 2 -4=-4 вершина находится в точке (0;-4)
Найдем корни уравнения x 2 -4=0
Неполное квадратное уравнение вида ax 2 +c=0. Чтобы его решить нужно неизвестные перенести в одну сторону, а известные в другую. x =±√(c/a)
x 2 =4
x 1 =2
x 2 =-2
Возьмем несколько произвольных точек, которые находятся рядом с вершиной х=0
х -2 -1 1 2
у 0 -3 -3 0
Подставляем вместо х в уравнение y= x 2 -4 значения
y=(-2) 2 -4=4-4=0
y=(-1) 2 -4=1-4=-3
y=1 2 -4=1-4=-3
y=2 2 -4=4-4=0
Видно по значениям функции,что парабола симметрична относительно прямой х=0
Подписывайтесь на канал на YOUTUBE , чтобы быть в курсе всех новинок и готовится с нами к экзаменам.
Конспект урока по алгебре для 8 класса средней общеобразовательной школы
Тема урока : Функция
Цель урока:
· Образовательная: определить понятие квадратичной функции вида (сравнить графики функций и ), показать формулу нахождения координат вершины параболы (научить применять данную формулу на практике); сформировать умение определения свойств квадратичной функции по графику (нахождение оси симметрии, координат вершины параболы, координат точек пересечения графика с осями координат).
· Развивающая : развитие математической речи, умения правильно, последовательно и рационально излагать свои мысли; развитие навыка правильной записи математического текста при помощи символов и обозначений; развитие аналитического мышления; развитие познавательной деятельности учащихся через умение анализировать, систематизировать и обобщать материал.
· Воспитательная : воспитание самостоятельности, умения выслушать других, формирование аккуратности и внимания в письменной математической речи.
Тип урока : изучение нового материала.
Методы обучения:
обобщенно-репродуктивный, индуктивно-эвристический.
Требования к знаниям и умениям учащихся
знать, что такое квадратичная функция вида , формулу нахождения координат вершины параболы; уметь находить координаты вершины параболы, координаты точек пересечения графика функции с осями координат, по графику функции определять свойства квадратичной функции.
Оборудование :
План урока
I. Организационный момент (1-2 мин)
II. Актуализация знаний (10 мин)
III. Изложение нового материала (15 мин)
IV. Закрепление нового материала (12 мин)
V. Подведение итогов (3 мин)
VI. Задание на дом (2 мин)
Ход урока
I. Организационный момент
Приветствие, проверка отсутствующих, сбор тетрадей.
II. Актуализация знаний
Учитель : На сегодняшнем уроке мы изучим новую тему: "Функция ". Но для начала повторим ранее изученный материал.
Фронтальный опрос:
1) Что называется квадратичной функцией? (Функция , где заданные действительные числа, , действительная переменная, называется квадратичной функцией.)
2) Что является графиком квадратичной функции? (Графиком квадратичной функции является парабола.)
3) Что такое нули квадратичной функции? (Нули квадратичной функции – значения , при которых она обращается в нуль.)
4) Перечислите свойства функции . (Значения функции положительны при и равно нулю при ; график функции симметричен относительно ос ординат; при функция возрастает, при - убывает.)
5) Перечислите свойства функции . (Если , то функция принимает положительные значения при , если , то функция принимает отрицательные значения при , значение функции равно 0 только; парабола симметрична относительно оси ординат; если , то функция возрастает при и убывает при , если , то функция возрастает при , убывает – при .)
III. Изложение нового материала
Учитель : Приступим к изучению нового материала. Откройте тетради, запишите число и тему урока. Обратите внимание на доску.
Запись на доске : Число.
Функция .

Учитель : На доске вы видите два графика функций. Первый график , а второй . Давайте попробуем сравнить их.
Свойства функции вы знаете. На их основании, и сравнивая наши графики, можно выделить свойства функции .
Итак, как вы думаете, от чего будет зависеть направление ветвей параболы ?
Ученики: Направление ветвей обеих парабол будет зависеть от коэффициента .
Учитель: Совершенно верно. Так же можно заметить, что у обеих парабол есть ось симметрии. У первого графика функции, что является осью симметрии?
Ученики: У параболы вида осью симметрии является ось ординат.
Учитель: Верно. А что является осью симметрии параболы
Ученики: Осью симметрии параболы является линия, которая проходит через вершину параболы, параллельно оси ординат.
Учитель : Правильно. Итак, осью симметрии графика функции будем называть прямую, проходящую через вершину параболы, параллельную оси ординат.
А вершина параболы – это точка с координатами . Они определяются по формуле:
Запишите формулу в тетрадь и обведите в рамочку.
Запись на доске и в тетрадях
Координаты вершины параболы.
Учитель : Теперь, чтобы было более понятно, рассмотрим пример.
Пример 1 : Найдите координаты вершины параболы .
Решение: По формуле
Учитель : Как мы уже отметили, ось симметрии проходит через вершину параболы. Посмотрите на доску. Начертите этот рисунок в тетради.
Запись на доске и в тетрадях:

Учитель: На чертеже: - уравнение оси симметрии параболы с вершиной в точке , где абсцисса вершины параболы.
Рассмотрим пример.
Пример 2: По графику функции определите уравнение оси симметрии параболы.

Уравнение оси симметрии имеет вид: , значит, уравнение оси симметрии данной параболы .
Ответ: - уравнение оси симметрии.
IV.Закрепление нового материала
Учитель : На доске записаны задания, которые необходимо решить в классе.
Запись на доске : № 609(3), 612(1), 613(3)
Учитель: Но сначала решим пример не из учебника. Решать будем у доски.
Пример 1: Найти координаты вершины параболы
![]()
Решение: По формуле
Ответ: координаты вершины параболы.
Пример 2: Найти координаты точек пересечения параболы ![]() с осями координат.
с осями координат.
Решение: 1) С осью :
Т.е. ![]()
По теореме Виета:
Точки пересечения с осью абсцисс (1;0) и (2;0).
2) С осью :
Точка пересечения с осью ординат (0;2).
Ответ: (1;0), (2;0), (0;2) – координаты точек пересечения с осями координат.
Урок по теме «Функция y=ax^2, ее график и свойства» изучается в курсе алгебры 9 класса в системе уроков по теме «Функции». Данный урок требует тщательной подготовки. А именно, таких методов и средств обучения, которые дадут поистине хорошие результаты.
Автор данного видеоурока позаботился о том, чтобы помочь учителям при подготовке к урокам по этой теме. Он разработал видеоурок с учетом всех требований. Материал подобран по возрасту школьников. Он не перегружен, но достаточно емок. Автор подробно рассказывает материал, останавливаясь на более важных моментах. Каждый теоретический пункт сопровождается примером, чтобы восприятие учебного материала было гораздо эффективнее и качественнее.
Урок может быть использован учителем на обычном уроке алгебры в 9 классе в качестве определенного этапа урока - объяснение нового материала. Учителю не придется в этот период ничего говорить или рассказывать. Ему достаточно включить этот видеоурок и следить за тем, чтобы обучающиеся внимательно слушали и записывали важные моменты.
Урок может использоваться и школьниками при самостоятельной подготовке к уроку, а также для самообразования.

Длительность урока составляет 8:17 минут. В начале урока автор замечает, что одной из важных функций является квадратичная функция. Затем вводится квадратичная функция с математической точки зрения. Дается ее определение с пояснениями.
Далее автор знакомит обучающихся с областью определения квадратичной функции. На экране появляется правильная математическая запись. После этого автор рассматривает пример квадратичной функции на реальной ситуации: за основу взята физическая задача, где показано, как зависит путь от времени при равноускоренном движении.

После этого автор рассматривает функцию y=3x^2. На экране появляется построение таблицы значений этой функции и функции y=x^2. Согласно данным этих таблиц строятся графики функций. Здесь же в рамке появляется пояснение, как получается график функции y=3x^2 из y=x^2.
Рассмотрев два частных случая, примера функции y=ax^2, автор приходит к правилу, как получается график этой функции из графика y=x^2.
Далее рассматривается функция y=ax^2, где a<0. И, подобно тому, как строились графики функций до этого, автор предлагает построить график функции y=-1/3 x^2. При этом он строит таблицу значений, строит графики функций y=-1/3 x^2 и, замечая при этом закономерность расположения графиков между собой.

Затем из свойств выводятся следствия. Их четыре. Среди них появляется новое понятие - вершины параболы. Далее следует замечание, где говорится, какие преобразования возможны для графика данной функции. После этого говорится о том, как получается график функции y=-f(x) из графика функции y=f(x), а также y=af(x) из y=f(x).
На этом урок, содержащий учебный материал заканчивается. Остается его закрепить, подобрав соответствующие задания в зависимости от способностей обучающихся.
Описание видеоурока
Рассмотрим некоторые частные случаи квадратичной функции.
Первый случай. Выясним, что представляет собой график функции игрек равно одна третья икс квадрат плюс четыре.
Для этого в одной системе координат построим графики функций игрек равно одна третья икс квадрат.. и..игрек равно одна третья икс квадрат плюс четыре.
Составим таблицу значений функции игрек равно одна третья икс квадрат. Построим по заданным точкам график функции.
Чтобы получить таблицу значений функции игрек равно одна третья икс квадрат плюс четыре при тех же значениях аргумента, следует к найденным значениям функции игрек равно одна третья икс квадрат.. прибавить четыре.
Составим таблицу значений для графика функции игрек равно одна третья икс квадрат плюс четыре. Построим по указанным координатам точки и соединим их плавной линией. Получим график функции игрек равно одна третья икс квадрат плюс четыре.
Легко понять, что график функции игрек равно одна третья икс квадрат плюс четыре можно получить из графика функции игрек равно одна третья икс квадрат с помощью параллельного переноса на четыре единицы вверх вдоль оси игрек.
Таким образом, график функции игрек равно а икс квадрат плюс эн является параболой, которая получается из графика функции игрек равно а икс квадрат с помощью параллельного переноса вдоль оси игрек на модуль эн единиц вверх, если эн больше нуля или вниз, если эн меньше нуля.
Второй случай. Рассмотрим функцию игрек равно одна третья квадрата разности чисел икс и шесть и построим ее график.
Построим таблицу значений функции игрек равно одна третья икс квадрат, укажем полученные точки на координатной плоскости и соединим плавной линией.
Теперь составим таблицу значений для функции игрек равно одна третья квадрата разности чисел икс и шесть. По указанным точкам построим график функции.
Заметно, что каждая точка второго графика получается из соответствующей точки первого графика с помощью параллельного переноса на шесть единиц вдоль оси икс.
График функции игрек равно а умноженное на квадрат разности икс и эм.. является параболой, которую можно получить из графика функции игрек равно а икс квадрат с помощью параллельного переноса вдоль оси икс на модуль эм единиц влево, если эм больше нуля или на модуль эм единиц вправо, если эм меньше нуля.
Рассмотрим теперь график функции игрек равно одна третья умножить на квадрат разности икс и два плюс пять. Ее график можно получить из графика функции игрек равно одна третья икс квадрат с помощью двух параллельных переносов - сдвига параболы вправо на две единицы и вверх на пять единиц.
При этом производить параллельные переносы можно в любом порядке: сначала выполнить вдоль оси икс, а затем вдоль оси игрек или наоборот.
Но почему при добавлении к функции числа эн ее график перемещается на модуль эн единиц вверх, если эн больше нуля или вниз, если эн меньше нуля, а при добавлении числа эм к аргументу, функция перемещается на модуль эм единиц вправо, если эм меньше нуля или влево, если эм больше нуля?
Рассмотрим первый случай. Пусть требуется построить график функции игрек равно эф от икс.. плюс эн. Заметим, что ординаты этого графика для всех значений аргумента на эн единиц больше соответствующих ординат графика игрек равно эф от икс при положительном эн и на эн единиц меньше при отрицательном эн. Следовательно, график функции игрек равно эф от икс…плюс эн можно получить параллельным переносом вдоль оси ординат графика функции игрек равно эф от икс на модуль эн единиц вверх, если эн больше нуля и на модуль эн единиц вниз, если эн меньше нуля.
Рассмотрим второй случай. Пусть требуется построить график функции игрек равно эф от суммы икс и эм. Рассмотрим функцию игрек равно эф от икс, которая в некоторой точке икс равной икс первое принимает значение игрек первое равно эф от икс первое. Очевидно, что функция игрек равно эф от суммы икс и эм примет такое же значение в точке икс второе, координата которой определяется из равенства икс второе плюс эм равно икс первое, то есть икс певрое равно икс первое минус эм. Причем рассматриваемое равенство справедливо для всех значений икс из области определения функции. Следовательно, график функции может быть получен параллельным перемещением графика функции игрек равно эф от икс вдоль оси абсцисс влево на модуль эм единиц влево, если эм больше нуля и на модуль эм вправо, если эм меньше нуля. Параллельное перемещение графика функции вдоль оси икс на эм единиц эквивалентно переносу оси игрек на столько же единиц, но в противоположную сторону.
При вращении параболы вокруг ее оси получается фигура, которую называют параболоидом. Если внутреннюю поверхность параболоида сделать зеркальной и направить на нее пучок лучей, параллельных оси симметрии параболы, то отраженные лучи соберутся в точке, которую называют фокусом. В то же время если источник света поместить в фокусе, то отраженные от зеркальной поверхности параболоида лучи окажутся параллельными и не рассеиваются.
Первое свойство позволяет получить в фокусе параболоида высокую температуру. Согласно легенде это свойство использовал древнегреческий ученый Архимед. При защите Сиракуз в войне против римлян он построил систему параболических зеркал, которая позволила сфокусировать отраженные солнечные лучи на кораблях римлян. В результате температура в фокусах параболических зеркал оказалась настолько высокой, что на кораблях вспыхнул пожар, и они сгорели. Также это свойство используется при изготовлении параболических антенн.
Второе свойство используется при изготовлении прожекторов и автомобильных фар.