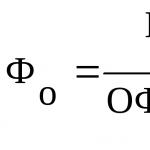Закон пропорциональности удлинения пружины приложенной силе был открыт английским физиком Робертом Гуком (1635-1703г.)
Научные интересы Гука были столь широки, что он часто не успевал доводить свои исследования до конца. Это давало повод к острейшим спорам о приоритете в открытии тех или иных законов с крупнейшими учеными (Гюйгенс, Ньютоном и др.). Однако закон Гука был настолько убедительно обоснован многочисленными периментами, что тут приоритет Гука никогда не оспаривался.
Теория пружины Роберта Гука:
В этом и состоит закон Гука!
РЕШЕНИЕ ЗАДАЧ
Определить жесткость пружины, которая под действием силы 10 Н удлинилась на 5 см.
Дано:
g = 10 H/кг
F = 10H
X = 5см = 0,05м
Найти:
k = ?

Груз находится в равновесии.

Ответ: жесткость пружины k = 200H/м.
ЗАДАЧА НА "5"
(сдаем на листочке).
Объясните, почему безопасен прыжок акробата на сетку батута с большой высоты? (призываем на помощь Роберта Гука)
С нетерпением жду ответа!
МАЛЕНЬКИЙ ОПЫТ
Поставьте вертикально резиновую трубку, на которую предварительно туго надето металлическое кольцо, и растяните трубку. Что при этом произойдет с кольцом?
Динамика - Класс!ная физика
Многие ли из нас задумывались, каким удивительным образом ведут себя предметы при воздействии на них?
Например, почему ткань, если мы растягиваем ее в разные стороны, может долго тянуться, а в один момент вдруг порваться? И почему тот же самый эксперимент куда сложнее провести с карандашом? От чего зависит сопротивление материала? Каким образом можно определить, до какой степени он поддается деформации или растяжению?
Все эти и многие другие вопросы более 300 лет назад задавал себе английский исследователь И нашел ответы, ныне объединенные под общим названием "Закон Гука".
Согласно его исследованиям, каждый материал имеет так называемый коэффициент упругости . Это свойство, позволяющее материалу растягиваться в определенных пределах. Коэффициент упругости - величина постоянная. Это значит, что каждый материал может выдержать лишь определенный уровень сопротивления, после чего он достигает уровня необратимой деформации.
В целом, Закон Гука можно выразить формулой:
где F - сила упругости, k - уже упомянутый коэффициент упругости, а /x/ - изменение длины материала. Что подразумевается под изменением этого показателя? Под воздействием силы некий изучаемый предмет, будь это струна, резина или любой другой, изменяются, вытягиваясь или сжимаясь. Изменением длины в данном случае считается разница между изначальной и конечной длиной изучаемого предмета. То есть то, на сколько вытянулась/сжалась пружина (резина, струна и т.д.)
Отсюда, зная длину и постоянный коэффициент упругости для данного материала, можно найти силу, с которой материал натягивается, или силу упругости, как еще нередко называют Закон Гука.
Существуют также особые случаи, при которых данный закон в своей стандартной форме использован быть не может. Речь идет об измерении силы деформации в условиях сдвига, то есть в ситуациях, когда деформацию производит некая сила, воздействующая на материал под углом. Закон Гука при сдвиге может быть выражен таким образом:
где τ - искомая сила, G- постоянный коэффициент, известный как модуль упругости при сдвиге, y - угол сдвига, та величина, на которую изменился угол наклона предмета.
Законом Гука обычно называют линейные соотношения между компонентами деформаций и компонентами напряжений.
Возьмем элементарный прямоугольный параллелепипед с гранями, параллельными координатным осям, нагруженный нормальным напряжением σ х , равномерно распределенным по двум противоположным граням (рис. 1). При этом σ y = σ z = τ х y = τ х z = τ yz = 0.
Вплоть до достижения предела пропорциональности относительное удлинение дается формулой
где Е — модуль упругости при растяжении. Для стали Е = 2*10 5 МПа , поэтому деформации очень малы и измеряются в процентах или в 1*10 5 (в тензометрических приборах, измеряющих деформации).
Удлинение элемента в направлении оси х сопровождается его сужением в поперечном направлении, определяемом компонентами деформаций
где μ - константа, называемая коэффициентом поперечного сжатия или коэффициентом Пуассона. Для стали μ обычно принимается равным 0,25-0,3.
Если рассматриваемый элемент нагружен одновременно нормальными напряжениями σ x , σ y , σ z , равномерно распределенными по его граням, то добавляются деформации

Производя наложение компонент деформации, вызванных каждым из трех напряжений, получим соотношения

Эти соотношения подтверждаются многочисленными экспериментами. Примененный метод наложения или суперпозиции для отыскания полных деформаций и напряжений, вызванных несколькими силами, является законным, пока деформации и напряжения малы и линейно зависят от приложенных сил. В таких случаях мы пренебрегаем малыми изменениями размеров деформируемого тела и малыми перемещениями точек приложения внешних сил и основываем наши вычисления на начальных размерах и начальной форме тела.

Следует отметить, что из малости перемещений еще не следует линейность соотношений между силами и деформациями. Так, например, в сжатом силами Q стержне, нагруженном дополнительно поперечной силой Р , даже при малом прогибе δ возникает дополнительный момент М = Qδ , который делает задачу нелинейной. В таких случаях полные прогибы не являются линейными функциями усилий и не могут быть получены с помощью простого наложения (суперпозиции).
Экспериментально установлено, что если касательные напряжения действуют по всем граням элемента, то искажение соответствующего угла зависит только от соответствующих компонентов касательного напряжения.
Константа G называется модулем упругости при сдвиге или модулем сдвига.
Общий случай деформации элемента от действия на него трех нормальных и трех касательных компонентов напряжений можно получить с помощью наложения: на три линейные деформации, определяемые выражениями (5.2а), накладываются три деформации сдвига, определяемые соотношениями (5.2б). Уравнения (5.2а) и (5.2б) определяют связь между компонентами деформаций и напряжений и называются обобщенным законом Гука . Покажем теперь, что модуль сдвига G выражается через модуль упругости при растяжении Е и коэффициент Пуассона μ . Для этого рассмотрим частный случай, когда σ х = σ , σ y = -σ и σ z = 0.
Вырежем элемент abcd плоскостями, параллельными оси z и наклоненными под углом 45° к осям х и у (рис. 3). Как следует из условий равновесия элемента 0bс , нормальные напряжения σ v на всех гранях элемента abcd равны нулю, а касательные напряжения равны

Такое напряженное состояние называется чистым сдвигом . Из уравнений (5.2а) следует, что

то есть удлинение горизонтального элемента 0c равно укорочению вертикального элемента 0b : ε y = -ε x .
Угол между гранями аb и bc изменяется, и соответствующую величину деформации сдвига γ можно найти из треугольника 0bс :

Отсюда следует, что

Виды деформаций
Деформацией называют изменение формы, размеров или объема тела. Деформация может быть вызвана действием на тело приложенных к нему внешних сил. Деформации, полностью исчезающие после прекращения действия на тело внешних сил, называют упругими , а деформации, сохраняющиеся и после того, как внешние силы перестали действовать на тело, - пластическими . Различают деформации растяжения или сжатия (одностороннего или всестороннего), изгиба , кручения и сдвига .
Силы упругости
При деформациях твердого тела его частицы (атомы, молекулы, ионы), находящиеся в узлах кристаллической решетки, смещаются из своих положений равновесия. Этому смещению противодействуют силы взаимодействия между частицами твердого тела, удерживающие эти частицы на определенном расстоянии друг от друга. Поэтому при любом виде упругой деформации в теле возникают внутренние силы, препятствующие его деформации.
Силы, возникающие в теле при его упругой деформации и направленные против направления смещения частиц тела, вызываемого деформацией, называют силами упругости. Силы упругости действуют в любом сечении деформированного тела, а также в месте его контакта с телом, вызывающим деформации. В случае одностороннего растяжения или сжатия сила упругости направлена вдоль прямой, по которой действует внешняя сила, вызывающая деформацию тела, противоположно направлению этой силы и перпендикулярно поверхности тела. Природа упругих сил электрическая.
Мы рассмотрим случай возникновения сил упругости при одностороннем растяжении и сжатии твердого тела.
Закон Гука
Связь между силой упругости и упругой деформацией тела (при малых деформациях) была экспериментально установлена современником Ньютона английским физиком Гуком. Математическое выражение закона Гука для деформации одностороннего растяжения (сжатия) имеет вид:
где f - сила упругости; х - удлинение (деформация) тела; k - коэффициент пропорциональности, зависящий от размеров и материала тела, называемый жесткостью. Единица жесткости в СИ - ньютон на метр (Н/м).
Закон Гука для одностороннего растяжения (сжатия) формулируют так: сила упругости, возникающая при деформации тела, пропорциональна удлинению этого тела.
Рассмотрим опыт, иллюстрирующий закон Гука. Пусть ось симметрии цилиндрической пружины совпадает с прямой Ах (рис. 20, а). Один конец пружины закреплен в опоре в точке А, а второй свободен и к нему прикреплено тело М. Когда пружина не деформирована, ее свободный конец находится в точке С. Эту точку примет за начало отсчета координаты х, определяющей положение свободного конца пружины.
Растянем пружину так, чтобы ее свободный конец находился в точке D, координата которой х > 0: В этой точке пружина действует на тело М упругой силой
Сожмем теперь пружину так, чтобы ее свободный конец находился в точке В, координата которой х
Из рисунка видно, что проекция силы упругости пружины на ось Ах всегда имеет знак, противоположный знаку координаты х, так как сила упругости направлена всегда к положению равновесия С. На рис. 20, б изображен график закона Гука. На оси абсцисс откладывают значения удлинения х пружины, а на оси ординат - значения силы упругости. Зависимость fх от х линейная, поэтому график представляет собой прямую, проходящую через начало координат.
Рассмотрим еще один опыт .
Пусть один конец тонкой стальной проволоки закреплен на кронштейне, а к другому концу подвешен груз, вес которого является внешней растягивающей силой F, действующей на проволоку перпендикулярно ее поперечному сечению (рис. 21).
Действие этой силы на проволоку зависит не только от модуля силы F, но и от площади поперечного сечения проволоки S.
Под действием приложенной к ней внешней силы проволока деформируется, растягивается. При не слишком большом растяжении эта деформация является упругой. В упруго деформированной проволоке возникает сила упругости f уп. Согласно третьему закону Ньютона, сила упругости равна по модулю и противоположна по направлению внешней силе, действующей на тело, т. е.
f уп = -F (2.10)
Состояние упруго деформированного тела характеризуют величиной s, называемой нормальным механическим напряжением (или, для краткости, просто нормальным напряжением ). Нормальное напряжение s равно отношению модуля силы упругости к площади поперечного сечения тела:
s = f уп /S (2.11)
Пусть первоначальная длина нерастянутой проволоки составляла L 0 . После приложения силы F проволока растянулась и ее длина стала равной L. Величину DL = L - L 0 называют абсолютным удлинением проволоки . Величину e = DL/L 0 (2.12) называют относительным удлинением тела . Для деформации растяжения e>0, для деформации сжатия e < 0.
Наблюдения показывают, что при небольших деформациях нормальное напряжение s пропорционально относительному удлинению e:
s = E|e|. (2.13)
Формула (2.13) является одним из видов записи закона Гука для одностороннего растяжения (сжатия). В этой формуле относительное удлинение взято по модулю, так как оно может быть и положительным и отрицательным. Коэффициент пропорциональности Е в законе Гука называется модулем продольной упругости (модулем Юнга).
Установим физический смысл модуля Юнга . Как видно из формулы (2.12), e = 1 и L = 2L 0 при DL = L 0 . Из формулы (2.13) следует, что в этом случае s = Е. Следовательно, модуль Юнга численно равен такому нормальному напряжению, которое должно было бы возникнуть в теле при увеличении его длины в 2 раза. (если бы для такой большой деформации выполнялся закон Гука). Из формулы (2.13) видно также, что в СИ модуль Юнга выражают в паскалях (1 Па = 1 Н/м 2).
Закон Гука формулируется так: сила упругости, которая возникает при деформации тела, вследствие приложения сторонних сил, пропорционально его удлинению. Деформация в свою очередь это изменение межатомных или межмолекулярных расстояние вещества под действием внешних сил. Сила упругости это сила, которая стремится вернуть эти атомы или молекулы в состояние равновесия.
Формула 1 - Закон Гука.
F - Сила упругости.
k - жесткость тела (Коэффициент пропорциональности, который зависит от материала тела и его формы).
x - Деформация тела (удлинение или сжатие тела).
Этот закон был открыт Робертом Гуком в 1660г. Он провел опыт, который заключался в том что. Тонкая стальная струна была закреплена одним концом, а ко второму концу прикладывалось различное усилие. Проще говоря, струна была подвешена к потолку, и к ней прикладывался груз различной массы.

Рисунок 1 - Растяжение струны под действием силы тяжести.
В результате опыта Гук выяснил, что в небольших приделах зависимость растяжения тела линейна относительно силы упругость. То есть при приложении единицы силы, тело удлиняется, на единицу длинны.

Рисунок 2 - График зависимости силы упругости от удлинения тела.
Нуль на графике это исходная длинна тела. Все что справа это увеличение длинны тела. Сила упругости при этом имеет отрицательное значение. То есть она стремиться вернуть тело в исходное состояние. Соответственно направлена встречно деформирующей силе. Все что слева сжатие тела. Сила упругости положительна.
Растяжение струны зависти не только от внешней силы, но и от сечения струны. Тонкая струна еще как-то растянется от небольшого веса. А вот если взять струну, той же длинны, но диаметром скажем в 1 м. То сложно себе представить какой вес потребуется для ее растяжения.
Для оценки того как сила действует на тело определенного сечения вводится понятие нормальное механическое напряжение.
Формула 2 - нормальное механическое напряжение.
S-Площадь поперечного сечения.
Это напряжение, в конечном счете, пропорционально относительному удлинению тела. Относительное удлинение это отношение приращения длинны тела к его общей длине. А коэффициент пропорциональности называется модулем Юнга. Модуль потому что значение удлинение тела берется по модулю, без учета знака. Не берется во внимание, укорачивается тело или удлиняется. Важно изменение его длинны.
Формула 3 - Модуль Юнга.
|e|- Относительное удлинение тела.
s- нормальное напряжение тела.