Dnes priatelia nebudú žiadne sople a sentimentalita. Namiesto toho vás bez akýchkoľvek otázok pošlem do boja s jedným z najimpozantnejších protivníkov v kurze algebry pre 8-9 ročníkov.
Áno, všetko ste pochopili správne: hovoríme o nerovnostiach s modulom. Pozrieme sa na štyri základné techniky, pomocou ktorých sa dozviete, ako vyriešiť približne 90 % takýchto problémov. A čo zvyšných 10%? No, budeme o nich hovoriť v samostatnej lekcii. :)
Pred rozborom niektorej z techník by som vám však rád pripomenul dva fakty, ktoré už potrebujete vedieť. V opačnom prípade riskujete, že látku dnešnej lekcie vôbec nepochopíte.
Čo už potrebujete vedieť
Captain Obvious tak trochu naznačuje, že na vyriešenie nerovností modulu je potrebné poznať dve veci:
- Ako sa riešia nerovnosti;
- Čo je modul.
Začnime druhým bodom.
Definícia modulu
Všetko je tu jednoduché. Existujú dve definície: algebraická a grafická. Na začiatok - algebraické:
Definícia. Modul čísla $ x $ je buď samotné číslo, ak je nezáporné, alebo opačné číslo, ak pôvodné $ x $ je stále záporné.
Píše sa to takto:
\ [\ vľavo | x \ vpravo | = \ vľavo \ (\ začiatok (zarovnanie) & x, \ x \ ge 0, \\ & -x, \ x \ lt 0. \\\ koniec (zarovnanie) \ vpravo. \]
Zjednodušene povedané, modul je „číslo bez mínusu“. A práve v tejto dualite (niekde so začiatočným číslom netreba nič robiť, ale niekde tam treba odstrániť nejaké mínus) tkvie celý problém pre začínajúcich študentov.
Existuje aj geometrická definícia. Je tiež užitočné ho poznať, ale budeme sa naň odvolávať len v zložitých a niektorých špeciálnych prípadoch, kde je geometrický prístup vhodnejší ako algebraický (spoiler: dnes už nie).
Definícia. Na číselnej osi nech je vyznačený bod $ a $. Potom modul $ \ vľavo | x-a \ vpravo | $ je vzdialenosť od bodu $ x $ k bodu $ a $ na tejto priamke.
Ak nakreslíte obrázok, dostanete niečo takéto:
 Definícia grafického modulu
Definícia grafického modulu Tak či onak, jeho kľúčová vlastnosť okamžite vyplýva z definície modulu: modul čísla je vždy nezáporný... Táto skutočnosť sa bude niesť ako červená niť celým naším dnešným príbehom.
Riešenie nerovností. Metóda rozstupu
Teraz sa poďme zaoberať nerovnosťami. Je ich veľmi veľa, ale našou úlohou je teraz vedieť vyriešiť aspoň tie najjednoduchšie z nich. Tie, ktoré redukujú na lineárne nerovnosti ako aj metóda intervalov.
Na túto tému mám dve skvelé lekcie (mimochodom, veľmi, VEĽMI užitočné - odporúčam naštudovať):
- Metóda rozmiestnenia nerovností (najmä pozrite si video);
- Zlomkové racionálne nerovnosti sú obrovskou lekciou, ale potom už nebudete mať žiadne otázky.
Ak toto všetko viete, ak veta „prejdime od nerovnosti k rovnici“ vo vás nevyvoláva túžbu zabiť sa o stenu, potom ste pripravení: vitajte v pekle pri hlavnej téme hodiny. :)
1. Nerovnosti tvaru "Modul menší ako funkcia"
Toto je jedna z najbežnejších úloh s modulmi. Je potrebné vyriešiť nerovnosť formulára:
\ [\ vľavo | f \ vpravo | \ lt g \]
Funkcie $ f $ a $ g $ môžu byť čokoľvek, ale zvyčajne sú to polynómy. Príklady takýchto nerovností:
\ [\ začať (zarovnať) & \ doľava | 2x + 3 \ vpravo | \ lt x + 7; \\ & \ vľavo | ((x) ^ (2)) + 2x-3 \ vpravo | +3 \ vľavo (x + 1 \ vpravo) \ lt 0; \\ & \ vľavo | ((x) ^ (2)) - 2 \ vľavo | x \ vpravo | -3 \ vpravo | \ lt 2. \\\ koniec (zarovnanie) \]
Všetky sú vyriešené doslova v jednom riadku podľa schémy:
\ [\ vľavo | f \ vpravo | \ lt g \ Šípka vpravo -g \ lt f \ lt g \ quad \ vľavo (\ Šípka vpravo \ vľavo \ (\ začiatok (zarovnanie) & f \ lt g, \\ & f \ gt -g \\\ koniec (zarovnanie) \ vpravo. \ vpravo) \]
Je ľahké vidieť, že sa zbavíme modulu, ale namiesto toho dostaneme dvojitú nerovnosť (alebo, čo je to isté, systém dvoch nerovností). Tento prechod však zohľadňuje absolútne všetky možné problémy: ak je číslo pod modulom kladné, metóda funguje; ak je negatívny, stále funguje; a dokonca aj s najnevhodnejšou funkciou namiesto $ f $ alebo $ g $ bude metóda stále fungovať.
Prirodzene vyvstáva otázka: nemôže to byť jednoduchšie? Bohužiaľ, nemôžete. Toto je celá vlastnosť modulu.
Dosť však filozofovania. Poďme vyriešiť pár problémov:
Úloha. Vyriešte nerovnosť:
\ [\ vľavo | 2x + 3 \ vpravo | \ lt x + 7 \]
Riešenie. Takže máme pred sebou klasickú nerovnosť tvaru "modul je menší" - dokonca nie je čo transformovať. Pracujeme podľa algoritmu:
\ [\ začať (zarovnať) & \ doľava | f \ vpravo | \ lt g \ šípka doprava -g \ lt f \ lt g; \\ & \ vľavo | 2x + 3 \ vpravo | \ lt x + 7 \ šípka doprava - \ doľava (x + 7 \ doprava) \ lt 2x + 3 \ lt x + 7 \\\ koniec (zarovnanie) \]
Neponáhľajte sa otvárať zátvorky, pred ktorými je mínus: je celkom možné, že zo zhonu urobíte útočnú chybu.
\ [- x-7 \ lt 2x + 3 \ lt x + 7 \]
\ [\ vľavo \ (\ začiatok (zarovnanie) & -x-7 \ lt 2x + 3 \\ & 2x + 3 \ lt x + 7 \\ \ koniec (zarovnanie) \ vpravo. \]
\ [\ vľavo \ (\ začiatok (zarovnanie) & -3x \ lt 10 \\ & x \ lt 4 \\ \ koniec (zarovnanie) \ vpravo. \]
\ [\ vľavo \ (\ začiatok (zarovnanie) & x \ gt - \ frac (10) (3) \\ & x \ lt 4 \\ \ koniec (zarovnanie) \ vpravo. \]
Problém sa zredukoval na dve elementárne nerovnosti. Označme ich riešenia na rovnobežných číselných osách:
Priesečník mnohých
Priesečník týchto množín bude odpoveďou.
Odpoveď: $ x \ v \ vľavo (- \ frac (10) (3); 4 \ vpravo) $
Úloha. Vyriešte nerovnosť:
\ [\ vľavo | ((x) ^ (2)) + 2x-3 \ vpravo | +3 \ vľavo (x + 1 \ vpravo) \ lt 0 \]
Riešenie. Táto úloha je už trochu náročnejšia. Na začiatok oddeľme modul posunutím druhého výrazu doprava:
\ [\ vľavo | ((x) ^ (2)) + 2x-3 \ vpravo | \ lt -3 \ vľavo (x + 1 \ vpravo) \]
Je zrejmé, že opäť čelíme nerovnosti vo forme „modul je menej“, takže sa modulu zbavíme podľa už známeho algoritmu:
\ [- \ vľavo (-3 \ vľavo (x + 1 \ vpravo) \ vpravo) \ lt ((x) ^ (2)) + 2x-3 \ lt -3 \ vľavo (x + 1 \ vpravo) \]
Teraz pozor: niekto povie, že som trochu perverzný so všetkými týmito zátvorkami. Dovoľte mi však ešte raz pripomenúť, že naším kľúčovým cieľom je kompetentní vyriešiť nerovnosť a dostať odpoveď... Neskôr, keď si dokonale osvojíte všetko, čo je popísané v tejto lekcii, môžete byť zvrátení, ako chcete: otvárať zátvorky, pridávať mínusy atď.
Na začiatok sa zbavíme dvojitého mínus vľavo:
\ [- \ vľavo (-3 \ vľavo (x + 1 \ vpravo) \ vpravo) = \ vľavo (-1 \ vpravo) \ cdot \ vľavo (-3 \ vpravo) \ cdot \ vľavo (x + 1 \ vpravo) = 3 \ vľavo (x + 1 \ vpravo) \]
Teraz rozšírme všetky zátvorky v dvojitej nerovnosti:
Prechádzame k dvojitej nerovnosti. Tentoraz budú výpočty serióznejšie:
\ [\ left \ (\ begin (zarovnať) & ((x) ^ (2)) + 2x-3 \ lt -3x-3 \\ & 3x + 3 \ lt ((x) ^ (2)) + 2x -3 \\ \ koniec (zarovnanie) \ vpravo. \]
\ [\ vľavo \ (\ začiatok (zarovnanie) & ((x) ^ (2)) + 5x \ lt 0 \\ & ((x) ^ (2)) - x-6 \ gt 0 \\ \ koniec ( zarovnať) \ doprava. \]
Obe nerovnosti sú štvorcové a sú riešené metódou intervalov (preto hovorím: ak neviete čo to je, radšej moduly zatiaľ nezaberať). Prejdeme k rovnici v prvej nerovnosti:
\ [\ begin (align) & ((x) ^ (2)) + 5x = 0; \\ & x \ vľavo (x + 5 \ vpravo) = 0; \\ & ((x) _ (1)) = 0; ((x) _ (2)) = -5. \\\ koniec (zarovnanie) \]
Ako vidíte, výstupom je neúplná kvadratická rovnica, ktorú je možné vyriešiť elementárnym spôsobom. Teraz sa poďme zaoberať druhou nerovnosťou systému. Tam musíte použiť Vietovu vetu:
\ [\ begin (align) & ((x) ^ (2)) - x-6 = 0; \\ & \ vľavo (x-3 \ vpravo) \ vľavo (x + 2 \ vpravo) = 0; \\ & ((x) _ (1)) = 3; ((x) _ (2)) = - 2. \\\ koniec (zarovnanie) \]
Získané čísla označíme na dvoch rovnobežných čiarach (jedna pre prvú nerovnosť a samostatná pre druhú):
Opäť, keďže riešime sústavu nerovníc, zaujíma nás priesečník tieňovaných množín: $ x \ v \ vľavo (-5; -2 \ vpravo) $. Toto je odpoveď.
Odpoveď: $ x \ v \ vľavo (-5; -2 \ vpravo) $
Myslím, že po týchto príkladoch je schéma riešenia veľmi jasná:
- Vyriešte modul prenesením všetkých ostatných členov na opačnú stranu nerovnosti. Dostaneme teda nerovnosť tvaru $ \ left | f \ vpravo | \ lt g $.
- Vyriešte túto nerovnosť odstránením modulu, ako je opísané vyššie. V istom momente bude potrebné prejsť od dvojitej nerovnosti k systému dvoch nezávislých výrazov, z ktorých každý sa už dá riešiť samostatne.
- Nakoniec ostáva už len pretnúť riešenia týchto dvoch nezávislých výrazov – a je to, dostaneme konečnú odpoveď.
Podobný algoritmus existuje aj pre nerovnosti nasledujúceho typu, keď je modul väčší ako funkcia. Je tam však pár vážnych „ale“. Teraz si povieme niečo o týchto „ale“.
2. Nerovnosti tvaru "Modul je viac ako funkcia"
Vyzerajú takto:
\ [\ vľavo | f \ vpravo | \ gt g \]
Podobné ako predchádzajúce? Zdá sa. Napriek tomu sa takéto úlohy riešia úplne iným spôsobom. Formálne je schéma nasledovná:
\ [\ vľavo | f \ vpravo | \ gt g \ Šípka doprava \ doľava [\ začiatok (zarovnanie) & f \ gt g, \\ & f \ lt -g \\\ koniec (zarovnanie) \ doprava. \]
Inými slovami, uvažujeme o dvoch prípadoch:
- Najprv jednoducho ignorujeme modul - riešime obvyklú nerovnosť;
- Potom v skutočnosti modul rozšírime o znamienko mínus a potom obe strany nerovnosti vynásobíme −1, so znamienkom ja.
V tomto prípade sú možnosti kombinované s hranatou zátvorkou, t.j. pred nami je kombinácia dvoch požiadaviek.
Všimnite si ešte raz: máme pred sebou nie systém, ale agregát v odpovedi sa množiny spájajú, nepretínajú sa... To je zásadný rozdiel oproti predchádzajúcemu bodu!
Vo všeobecnosti majú mnohí študenti úplný zmätok s odbormi a priesečníkmi, takže poďme na to raz a navždy:
- "∪" je znakom spojenia. V skutočnosti ide o štylizované písmeno „U“, ktoré k nám prišlo anglického jazyka a je to skratka pre "Union", t.j. "Asociácie".
- „∩“ je značka križovatky. Toto svinstvo nevzniklo z ničoho nič, len sa objavilo ako opozícia k "∪".
Aby ste si to ešte ľahšie zapamätali, pridajte k týmto znakom nohy a vytvorte okuliare (len ma teraz neobviňujte z propagácie drogovej závislosti a alkoholizmu: ak vážne študujete túto lekciu, potom ste už drogovo závislý):
 Rozdiel medzi priesečníkom a zjednotením množín
Rozdiel medzi priesečníkom a zjednotením množín V preklade do ruštiny to znamená nasledovné: zväzok (súbor) obsahuje prvky z oboch súborov, teda nie menej ako každý z nich; ale priesečník (systém) zahŕňa len tie prvky, ktoré sú súčasne v prvej množine aj v druhej. Preto priesečník množín nie je nikdy väčší ako zdrojové množiny.
Takže to bolo jasnejšie? To je skvelé. Poďme sa pustiť do praxe.
Úloha. Vyriešte nerovnosť:
\ [\ vľavo | 3x + 1 \ vpravo | \ gt 5-4x \]
Riešenie. Postupujeme podľa schémy:
\ [\ vľavo | 3x + 1 \ vpravo | \ gt 5-4x \ Šípka doprava \ doľava [\ začiatok (zarovnanie) & 3x + 1 \ gt 5-4x \\ & 3x + 1 \ lt - \ doľava (5-4x \ doprava) \\\ koniec (zarovnanie) \ správny. \]
Vyriešte každú nerovnosť v populácii:
\ [\ vľavo [\ začiatok (zarovnanie) & 3x + 4x \ gt 5-1 \\ & 3x-4x \ lt -5-1 \\ \ koniec (zarovnanie) \ vpravo. \]
\ [\ vľavo [\ začiatok (zarovnanie) & 7x \ gt 4 \\ & -x \ lt -6 \\ \ koniec (zarovnanie) \ vpravo. \]
\ [\ vľavo [\ začať (zarovnať) & x \ gt 4/7 \ \\ & x \ gt 6 \\ \ koniec (zarovnať) \ vpravo. \]
Každú výslednú množinu označíme na číselnej osi a potom ich skombinujeme:
Spojenie množín
Odpoveď je jednoznačne $ x \ v \ vľavo (\ frac (4) (7); + \ infty \ vpravo) $
Odpoveď: $ x \ v \ vľavo (\ frac (4) (7); + \ infty \ vpravo) $
Úloha. Vyriešte nerovnosť:
\ [\ vľavo | ((x) ^ (2)) + 2x-3 \ vpravo | \ gt x \]
Riešenie. dobre? Nič - všetko je rovnaké. Od nerovnosti s modulom prejdeme k množine dvoch nerovností:
\ [\ vľavo | ((x) ^ (2)) + 2x-3 \ vpravo | \ gt x \ Šípka doprava \ doľava [\ begin (zarovnanie) & ((x) ^ (2)) + 2x-3 \ gt x \\ & ((x) ^ (2)) + 2x-3 \ lt -x \\\ koniec (zarovnanie) \ vpravo. \]
Riešime každú nerovnosť. Bohužiaľ, korene tam nebudú veľmi dobré:
\ [\ begin (align) & ((x) ^ (2)) + 2x-3 \ gt x; \\ & ((x) ^ (2)) + x-3 \ gt 0; \\ & D = 1 + 12 = 13; \\ & x = \ frac (-1 \ pm \ sqrt (13)) (2). \\\ koniec (zarovnanie) \]
V druhej nerovnosti je tiež malá hra:
\ [\ begin (align) & ((x) ^ (2)) + 2x-3 \ lt -x; \\ & ((x) ^ (2)) + 3x-3 \lt 0; \\ & D = 9 + 12 = 21; \\ & x = \ frac (-3 \ pm \ sqrt (21)) (2). \\\ koniec (zarovnanie) \]
Teraz musíte tieto čísla označiť na dvoch osiach - jednu os pre každú nerovnosť. Musíte však označiť body v správnom poradí: čím väčšie číslo, tým viac sa bod posunie doprava.
A tu nás čaká nastavenie. Ak sú čísla $ \ frac (-3- \ sqrt (21)) (2) \ lt \ frac (-1- \ sqrt (13)) (2) $ jasné (výrazy v čitateli prvého zlomku sú menej ako výrazy v čitateli druhého , takže súčet je tiež menší, s číslami $ \ frac (-3- \ sqrt (13)) (2) \ lt \ frac (-1+ \ sqrt (21) )) (2) $ nebudú žiadne ťažkosti (kladné číslo je samozrejme negatívnejšie), potom s posledným párom nie je všetko také jednoduché. Čo je viac: $ \ frac (-3+ \ sqrt (21)) (2) $ alebo $ \ frac (-1+ \ sqrt (13)) (2) $? Od odpovede na túto otázku bude závisieť usporiadanie bodov na číselných osách a vlastne aj odpoveď.
Tak porovnajme:
\ [\ begin (matica) \ frac (-1+ \ sqrt (13)) (2) \ vee \ frac (-3+ \ sqrt (21)) (2) \\ -1+ \ sqrt (13) \ vee -3+ \ sqrt (21) \\ 2+ \ sqrt (13) \ vee \ sqrt (21) \\\ koniec (matica) \]
Odstránili sme koreň, dostali sme nezáporné čísla na oboch stranách nerovnosti, takže máme právo odmocniť obe strany:
\ [\ begin (matica) ((\ vľavo (2+ \ sqrt (13) \ vpravo)) ^ (2)) \ vee ((\ vľavo (\ sqrt (21) \ vpravo)) ^ (2)) \ \ 4 + 4 \ sqrt (13) +13 \ vee 21 \\ 4 \ sqrt (13) \ vee 3 \\\ koniec (matica) \]
Myslím, že tu nie je na škodu, že $ 4 \ sqrt (13) \ gt 3 $, takže $ \ frac (-1+ \ sqrt (13)) (2) \ gt \ frac (-3+ \ sqrt (21) ) (2) $, nakoniec budú body na osiach umiestnené takto:
Prípad škaredých koreňov
Pripomínam, že riešime kolekciu, takže odpoveďou bude únia, nie priesečník tieňovaných množín.
Odpoveď: $ x \ v \ vľavo (- \ infty; \ frac (-3+ \ sqrt (21)) (2) \ vpravo) \ bigcup \ vľavo (\ frac (-1+ \ sqrt (13)) (2 ); + \ infty \ vpravo) $
Ako vidíte, naša schéma funguje skvele pre jednoduché aj veľmi ťažké úlohy. Jediná vec " slabosť»V tomto prístupe - musíte kompetentne porovnávať iracionálne čísla (a verte mi: to nie sú len korene). Ale problematike porovnávania bude venovaná samostatná (a veľmi vážna lekcia). A ideme ďalej.
3. Nerovnosti s nezápornými „chvostmi“
Tak sme sa dostali k zábavnej časti. Toto sú tvarové nerovnosti:
\ [\ vľavo | f \ vpravo | \ gt \ vľavo | g \ vpravo | \]
Vo všeobecnosti platí, že algoritmus, o ktorom budeme teraz hovoriť, je platný len pre modul. Funguje pri všetkých nerovnostiach, kde ľavá a pravá strana sú zaručene nezáporné výrazy:
Čo robiť s týmito úlohami? Len si pamätaj:
V nerovnostiach s nezápornými „chvostmi“ môžu byť obe strany pozdvihnuté na akúkoľvek prirodzenú silu. Nebudú žiadne ďalšie obmedzenia.
V prvom rade nás bude zaujímať kvadratúra - spaľuje moduly a korene:
\ [\ begin (zarovnať) & ((\ vľavo (\ vľavo | f \ vpravo | \ vpravo)) ^ (2)) = ((f) ^ (2)); \\ & ((\ vľavo (\ sqrt (f) \ vpravo)) ^ (2)) = f. \\\ koniec (zarovnanie) \]
Len si to nemýľte s extrakciou druhej odmocniny:
\ [\ sqrt (((f) ^ (2))) = \ vľavo | f \ vpravo | \ ne f \]
V momente, keď študent zabudol nainštalovať modul, sa stalo nespočetné množstvo chýb! Ale toto je úplne iný príbeh (sú to akoby iracionálne rovnice), takže sa tomu teraz nebudeme venovať. Poďme radšej vyriešiť pár problémov:
Úloha. Vyriešte nerovnosť:
\ [\ vľavo | x + 2 \ vpravo | \ ge \ vľavo | 1-2x \ vpravo | \]
Riešenie. Hneď si všimnime dve veci:
- Toto je voľná nerovnosť. Body na číselnej osi budú vyrazené.
- Obe strany nerovnosti sú určite nezáporné (toto je vlastnosť modulu: $ \ vľavo | f \ vľavo (x \ vpravo) \ vpravo | \ ge 0 $).
Preto môžeme odmocniť obe strany nerovnosti, aby sme sa zbavili modulu a vyriešili problém pomocou obvyklej intervalovej metódy:
\ [\ začať (zarovnať) & ((\ vľavo (\ vľavo | x + 2 \ vpravo | \ vpravo)) ^ (2)) \ ge ((\ vľavo (\ vľavo | 1-2x \ vpravo | \ vpravo) )^ (2)); \\ & ((\ vľavo (x + 2 \ vpravo)) ^ (2)) \ ge ((\ vľavo (2x-1 \ vpravo)) ^ (2)). \\\ koniec (zarovnanie) \]
V poslednom kroku som trochu podvádzal: zmenil som postupnosť členov pomocou parity modulu (v skutočnosti som výraz $ 1-2x $ vynásobil -1).
\ [\ begin (zarovnať) & ((\ vľavo (2x-1 \ vpravo)) ^ (2)) - ((\ vľavo (x + 2 \ vpravo)) ^ (2)) \ le 0; \\ & \ vľavo (\ vľavo (2x-1 \ vpravo) - \ vľavo (x + 2 \ vpravo) \ vpravo) \ cdot \ vľavo (\ vľavo (2x-1 \ vpravo) + \ vľavo (x + 2 \ vpravo) \ vpravo) \ le 0; \\ & \ vľavo (2x-1-x-2 \ vpravo) \ cdot \ vľavo (2x-1 + x + 2 \ vpravo) \ le 0; \\ & \ vľavo (x-3 \ vpravo) \ cdot \ vľavo (3x + 1 \ vpravo) \ le 0. \\\ koniec (zarovnať) \]
Riešime metódou intervalov. Prejdeme od nerovnosti k rovnici:
\ [\ začať (zarovnať) & \ vľavo (x-3 \ vpravo) \ vľavo (3x + 1 \ vpravo) = 0; \\ & ((x) _ (1)) = 3; ((x) _ (2)) = - \ frac (1) (3). \\\ koniec (zarovnanie) \]
Nájdené korene označíme na číselnej osi. Ešte raz: všetky bodky sú vyplnené, pretože pôvodná nerovnosť nie je striktná!
Zbavenie sa znamienka modulu
Dovoľte mi pripomenúť pre obzvlášť tvrdohlavých: berieme znamienka z poslednej nerovnosti, ktorá bola zapísaná pred prechodom na rovnicu. A natrite požadované oblasti v rovnakej nerovnosti. V našom prípade je to $ \ vľavo (x-3 \ vpravo) \ vľavo (3x + 1 \ vpravo) \ le 0 $.
Takže to je všetko. Problém bol vyriešený.
Odpoveď: $ x \ v \ vľavo [- \ frac (1) (3); 3 \ vpravo] $.
Úloha. Vyriešte nerovnosť:
\ [\ vľavo | ((x) ^ (2)) + x + 1 \ vpravo | \ le \ vľavo | ((x) ^ (2)) + 3x + 4 \ vpravo | \]
Riešenie. Všetci robíme to isté. Nebudem to komentovať - stačí sa pozrieť na postupnosť akcií.
Umocnenie:
\ [\ begin (zarovnať) & ((\ vľavo (\ vľavo | ((x) ^ (2)) + x + 1 \ vpravo | \ vpravo)) ^ (2)) \ le ((\ vľavo (\ vľavo | ((x) ^ (2)) + 3x + 4 \ vpravo | \ vpravo)) ^ (2)); \\ & ((\ vľavo (((x) ^ (2)) + x + 1 \ vpravo)) ^ (2)) \ le ((\ vľavo (((x) ^ (2)) + 3x + 4 \ vpravo)) ^ (2)); \\ & ((\ vľavo (((x) ^ (2)) + x + 1 \ vpravo)) ^ (2)) - ((\ vľavo (((x) ^ (2)) + 3x + 4 \ vpravo)) ^ (2)) \ le 0; \\ & \ vľavo (((x) ^ (2)) + x + 1 - ((x) ^ (2)) - 3x-4 \ vpravo) \ krát \\ & \ krát \ vľavo ((x) ^ (2)) + x + 1 + ((x) ^ (2)) + 3x + 4 \ vpravo) \ 0; \\ & \ vľavo (-2x-3 \ vpravo) \ vľavo (2 ((x) ^ (2)) + 4x + 5 \ vpravo) \ le 0. \\\ koniec (zarovnať) \]
Metóda medzier:
\ [\ začať (zarovnať) & \ vľavo (-2x-3 \ vpravo) \ vľavo (2 ((x) ^ (2)) + 4x + 5 \ vpravo) = 0 \\ & -2x-3 = 0 \ Šípka vpravo x = -1,5; \\ & 2 ((x) ^ (2)) + 4x + 5 = 0 \ Šípka vpravo D = 16-40 \ lt 0 \ Šípka vpravo \ varnothing. \\\ koniec (zarovnanie) \]
Len jeden koreň na číselnej osi:
Odpoveďou je celý interval
Odpoveď: $ x \ v \ vľavo [-1,5; + \ infty \ vpravo) $.
Rýchla poznámka k poslednej úlohe. Ako presne poznamenal jeden z mojich študentov, oba výrazy podmodulov v tejto nerovnosti sú zjavne kladné, takže znamienko modulu možno bez ujmy na zdraví vynechať.
Ale to je úplne iná úroveň myslenia a iný prístup - možno to podmienečne nazvať metódou dôsledkov. O ňom - v samostatnej lekcii. Teraz prejdime k poslednej časti dnešnej lekcie a pouvažujme nad univerzálnym algoritmom, ktorý vždy funguje. Aj keď sa všetky predchádzajúce prístupy ukázali ako bezmocné. :)
4. Metóda enumerácie možností
Ale čo ak všetky tieto techniky nefungujú? Ak sa nerovnosť nezredukuje na nezáporné chvosty, ak modul nemožno izolovať, ak vôbec bolesť-smútok-túžba?
Vtedy nastupuje na scénu „ťažké delostrelectvo“ všetkej matematiky – metóda hrubej sily. Čo sa týka nerovností s modulom, vyzerá to takto:
- Napíšte všetky výrazy submodulu a nastavte ich na nulu;
- Vyriešte získané rovnice a označte nájdené korene na jednej číselnej osi;
- Rovná čiara bude rozdelená na niekoľko sekcií, vo vnútri ktorých má každý modul pevný znak, a preto sa jednoznačne odvíja;
- Vyriešte nerovnosť na každom takomto mieste (pre spoľahlivosť môžete samostatne zvážiť hranice koreňov získané v odseku 2). Skombinujte výsledky - toto bude odpoveď. :)
Ako to je? slabý? Jednoducho! Len na dlho. Pozrime sa v praxi:
Úloha. Vyriešte nerovnosť:
\ [\ vľavo | x + 2 \ vpravo | \ lt \ vľavo | x-1 \ vpravo | + x- \ frac (3) (2) \]
Riešenie. Toto svinstvo nie je zredukované na nerovnosti ako $ \ left | f \ vpravo | \ lt g $, $ \ vľavo | f \ vpravo | \ gt g $ alebo $ \ vľavo | f \ vpravo | \ lt \ vľavo | g \ doprava | $, takže ideme rovno.
Vypíšeme výrazy podmodulov, prirovnáme ich k nule a nájdeme korene:
\ [\ začať (zarovnať) & x + 2 = 0 \ Šípka doprava x = -2; \\ & x-1 = 0 \ Šípka doprava x = 1. \\\ koniec (zarovnanie) \]
Celkovo máme dva korene, ktoré rozdeľujú číselnú os na tri časti, v rámci ktorých je každý modul jednoznačne odhalený:
Rozdelenie číselného riadku nulami submodulárnych funkcií
Pozrime sa na každú lokalitu samostatne.
1. Nech $ x \ lt -2 $. Potom sú oba výrazy submodulu záporné a pôvodnú nerovnosť možno prepísať takto:
\ [\ začiatok (zarovnanie) & - \ vľavo (x + 2 \ vpravo) \ lt - \ vľavo (x-1 \ vpravo) + x-1,5 \\ & -x-2 \ lt -x + 1 + x-1,5 \\ & x \ gt 1,5 \\\ koniec (zarovnanie) \]
Máme celkom jednoduché obmedzenie. Skrížime to s pôvodným predpokladom, že $ x \ lt -2 $:
\ [\ doľava \ (\ začiatok (zarovnanie) & x \ lt -2 \\ & x \ gt 1,5 \\\ koniec (zarovnanie) \ doprava. \ Šípka doprava x \ v \ varnothing \]
Je zrejmé, že premenná $ x $ nemôže byť súčasne menšia ako -2, ale väčšia ako 1,5. Na tejto stránke nie sú žiadne rozhodnutia.
1.1. Zvážte hraničný prípad samostatne: $ x = -2 $. Toto číslo len dosadíme do pôvodnej nerovnosti a skontrolujeme: je to pravda?
\ [\ začať (zarovnať) & ((\ vľavo. \ vľavo | x + 2 \ vpravo | \ lt \ vľavo | x-1 \ vpravo | + x-1,5 \ vpravo |) _ (x = -2) ) \\ & 0 \ lt \ vľavo | -3 \ vpravo | -2-1,5; \\ & 0 \ lt 3-3,5; \\ & 0 \ lt -0,5 \ Šípka doprava \ varnothing. \\\ koniec (zarovnanie) \]
Je zrejmé, že reťazec výpočtov nás priviedol k nesprávnej nerovnosti. Pôvodná nerovnosť je preto tiež nesprávna a $ x = -2 $ nie je zahrnuté v odpovedi.
2. Teraz nechajte $ -2 \ lt x \ lt 1 $. Ľavý modul sa už otvorí s „pluskom“, ale pravý je stále s „mínusom“. Máme:
\ [\ začiatok (zarovnanie) & x + 2 \ lt - \ vľavo (x-1 \ vpravo) + x-1,5 \\ & x + 2 \ lt -x + 1 + x-1,5 \\ & x \ lt -2,5 \\\ koniec (zarovnanie) \]
Opäť sa krížime s pôvodnou požiadavkou:
\ [\ doľava \ (\ začiatok (zarovnanie) & x \ lt -2,5 \\ & -2 \ lt x \ lt 1 \\\ koniec (zarovnanie) \ doprava. \ Šípka doprava x \ v \ varnothing \]
A opäť prázdna množina riešení, pretože neexistujú čísla, ktoré by boli súčasne menšie ako -2,5, ale väčšie ako -2.
2.1. A opäť špeciálny prípad: $ x = 1 $. Nahradiť v pôvodnej nerovnosti:
\ [\ začať (zarovnať) & ((\ vľavo. \ vľavo | x + 2 \ vpravo | \ lt \ vľavo | x-1 \ vpravo | + x-1,5 \ vpravo |) _ (x = 1)) \\ & \ vľavo | 3 \ vpravo | \ lt \ vľavo | 0 \ vpravo | + 1-1,5; \\ & 3 \ lt -0,5; \\ & 3 \ lt -0,5 \ Šípka doprava \ varnothing. \\\ koniec (zarovnanie) \]
Podobne ako v predchádzajúcom „špeciálnom prípade“ v odpovedi zjavne nie je zahrnuté číslo $ x = 1 $.
3. Posledný kus priamky: $ x \ gt 1 $. Tu sú všetky moduly rozšírené o znamienko plus:
\ [\ začiatok (zarovnanie) & x + 2 \ lt x-1 + x-1,5 \\ & x + 2 \ lt x-1 + x-1,5 \\ & x \ gt 4,5 \\ \ koniec (zarovnanie) \ ]
A opäť pretíname nájdenú množinu s pôvodným obmedzením:
\ [\ doľava \ (\ začiatok (zarovnanie) & x \ gt 4,5 \\ & x \ gt 1 \\\ koniec (zarovnanie) \ doprava. \ Šípka doprava x \ do \ doľava (4,5; + \ infty \ správny) \]
Konečne! Našli sme interval, ktorý bude odpoveďou.
Odpoveď: $ x \ v \ vľavo (4,5; + \ infty \ vpravo) $
Na záver jedna poznámka, ktorá vás môže zachrániť pred hlúpymi chybami pri riešení skutočných problémov:
Riešením nerovností s modulmi sú zvyčajne pevné množiny na číselnej osi – intervaly a segmenty. Izolované body sú oveľa menej bežné. A ešte menej často sa stáva, že hranice riešenia (koniec segmentu) sa zhodujú s hranicou uvažovaného rozsahu.
V dôsledku toho, ak nie sú v odpovedi zahrnuté hranice (tieto „špeciálne prípady“), potom takmer určite oblasti naľavo a napravo od týchto hraníc nebudú zahrnuté do odpovede. A naopak: do odpovede vstúpila hranica, čo znamená, že odpovede budú aj niektoré oblasti okolo nej.
Majte to na pamäti pri testovaní vašich riešení.
UVAŽOVANÉ
Pedagogickou radou ministerstva školstva
"Stredná škola Zashizhemskaya"
Protokol č.1
DOHODNUTÉ
Zástupca riaditeľa pre OIA
_______ / Sidorkina R.L. /
SCHVÁLENÉ
vedúci učiteľ:
A.P. Konakov
Objednávka č.63
Riešenie rovníc a nerovníc s modulom
Program zostavili:
vyšší učiteľ matematiky
Sidorkina R.L.
Obec Zashizhemye, 2014
Obsah
Úvod ………………………………………………………………… 3
Najjednoduchšie rovnice a nerovnice s modulom ………………………… 5
Grafické riešenie rovníc a nerovníc s modulom ………… .8
Iné spôsoby riešenia rovníc a nerovníc s modulom ... ... ...... 10
Záver ………………………………………………………… ..16
Referencie ……………………………………………………… 18
Úvod
Pojem absolútnej hodnoty (modulu) je jednou z najdôležitejších charakteristík čísla ako v oblasti reálnych, tak aj v oblasti komplexných čísel.
Tento koncept je široko používaný nielen v rôznych častiach školského kurzu matematiky, ale aj v kurzoch vyššej matematiky, fyziky a technických vied študovaných na univerzitách. Napríklad v teórii približných výpočtov sa používajú pojmy absolútnych a relatívnych chýb približného čísla. V mechanike a geometrii sa študujú pojmy vektor a jeho dĺžka (modul vektora). V matematickej analýze je pojem absolútnej hodnoty čísla obsiahnutý v definíciách takých základných pojmov, ako je limita, ohraničená funkcia atď. Problémy súvisiace s absolútnymi hodnotami sa často vyskytujú na matematických olympiádach, prijímacích skúškach na vysoké školy a jednotná štátna skúška. A preto bolo pre nás dôležité študovať niektoré aspekty tejto témy.
Hlavný cieľ našou prácou je študovať rôzne metódy riešenia rovníc a nerovníc s modulmi.
Tento cieľ by sa malo dosiahnuť pri riešení nasledujúceho úlohy:
Preskúmajte definíciu a niektoré vlastnosti modulu.
Osvojiť si riešenie najjednoduchších rovníc a nerovníc s modulom cez ekvivalentné prechody
Zvážte rôzne metódy riešenia rovníc a nerovníc s modulom.
Objekt výskumu sú niektoré typy rovníc a nerovníc s modulom.
Položka výskum - rôzne metódy riešenia rovníc a nerovníc s modulom, a to: grafická metóda, metóda geometrickej interpretácie, použitie identity, aplikácia znakovej vety, metóda prechodu na dôsledok, metóda intervalov, metóda násobenia kladným činiteľom, metóda rozširovania modulov.
Štúdia využívala metódy, ako je štúdium literatúry o táto záležitosť a praktická metóda.
Počas našej práce sme skúmali také zdroje ako:
1. „Veľká matematická encyklopédia“ pre školákov a študentov;
Matematika. Jednotná štátna skúška - 2011-2012. Typické možnosti skúšky. / Editoval A.L. Semenová, I.V. Jaščenko.
Encyklopédia „Poznám svet“ Matematika;
;
Najjednoduchšie rovnice a nerovnice s modulom
Najjednoduchšie rovnice budeme označovať ako rovnice vyriešené jedným z nasledujúcich ekvivalentných prechodov: 
Príklady riešenia najjednoduchších rovníc.
Príklad 1 Poďme vyriešiť rovnicu  .
.
Riešenie.
Odpoveď.  .
.
Príklad 2 Poďme vyriešiť rovnicu.
Riešenie.
Odpoveď.  .
.
Príklad 3 Poďme vyriešiť rovnicu  .
.
Riešenie.

Odpoveď.  .
.
Množstvo rovníc sa rieši pomocou nasledujúcej vety.
Veta 4 Súčet modulov sa rovná algebraickému súčtu submodulárnych veličín práve vtedy, ak má každá veličina rovnaké znamienko, s ktorým vstupuje do algebraického súčtu.
Príklad 5 Vyriešte rovnicu
Riešenie. Odvtedy máme rovnosť tvaru, kde  ,
,  ... Preto je pôvodná rovnica ekvivalentná systému:
... Preto je pôvodná rovnica ekvivalentná systému:

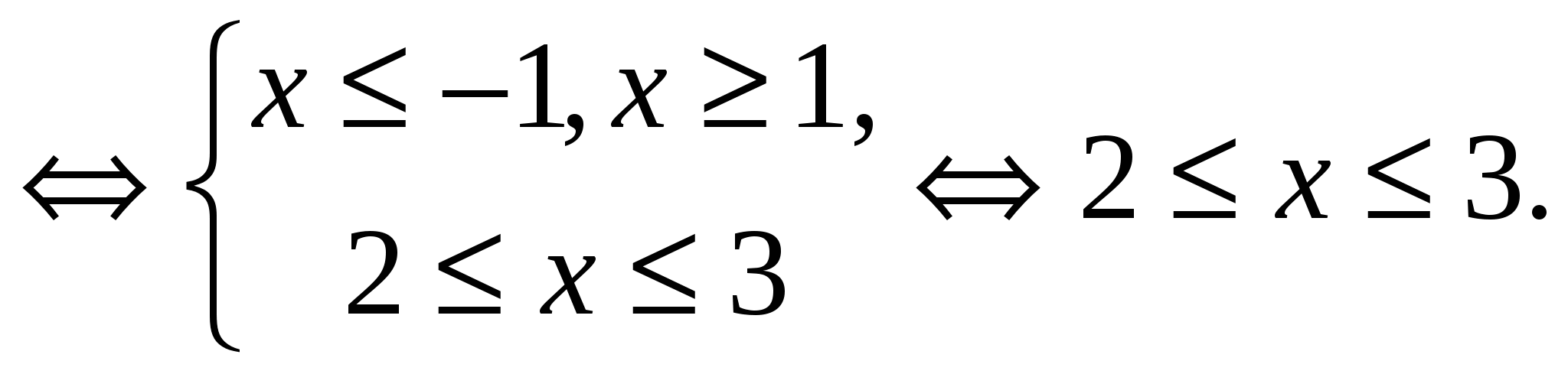
Odpoveď.  .
.
Príklady riešenia najjednoduchších nerovností.
Príklad 6 Vyriešte nerovnosť  .
.
Riešenie.
Odpoveď. 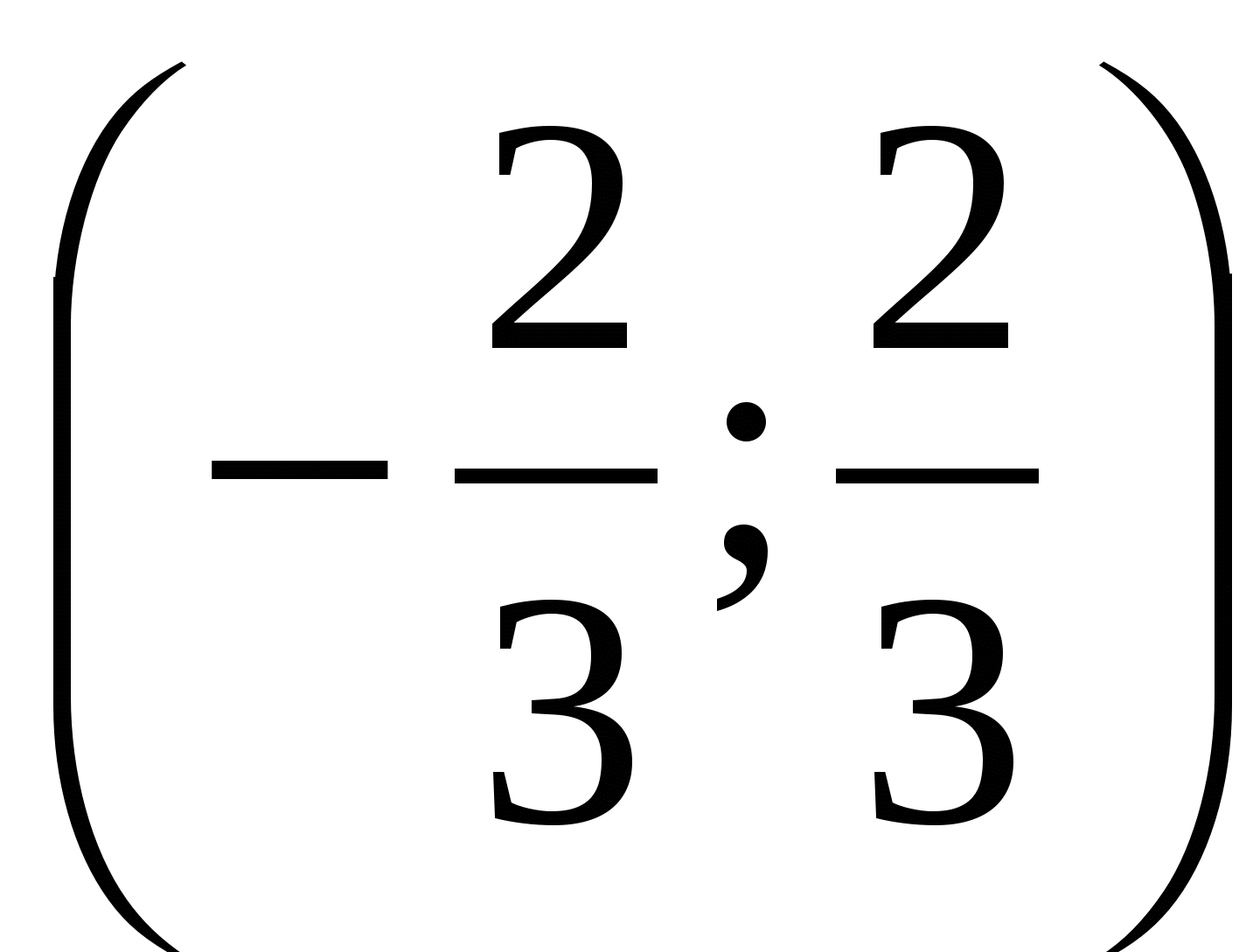 .
.
Príklad 7 Vyriešte nerovnosť  .
.
Riešenie.
Odpoveď.  .
.
Napodiv, ale 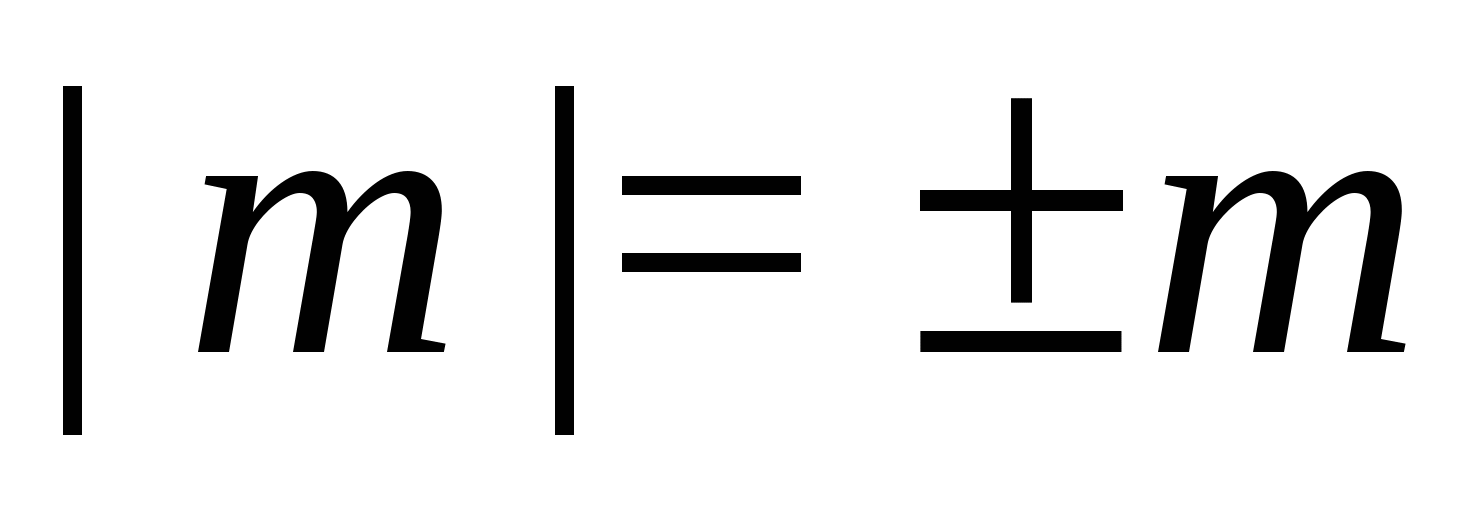 dosť na to, aby ste sa zbavili znamienka modulu v akýchkoľvek nerovnostiach.
dosť na to, aby ste sa zbavili znamienka modulu v akýchkoľvek nerovnostiach.
Príklad 8 Vyriešte nerovnosť
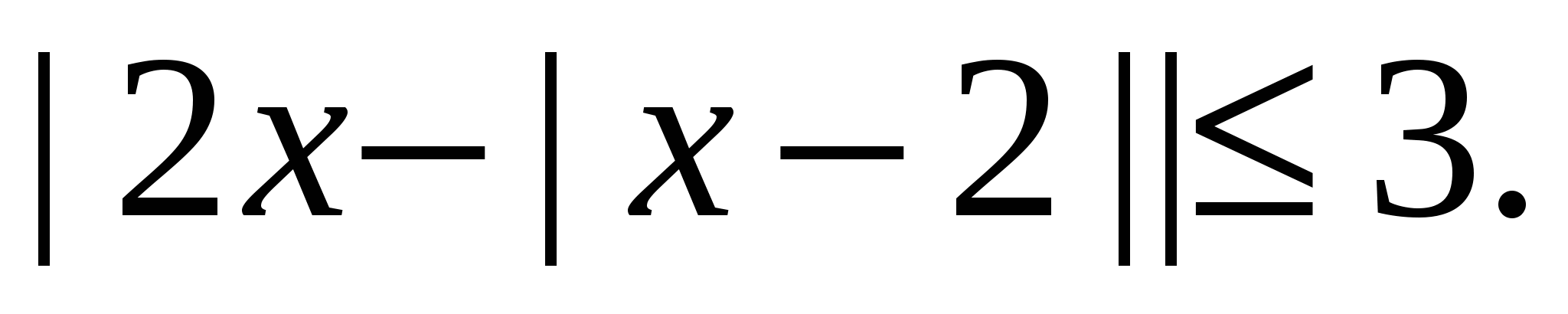
Riešenie.



Odpoveď.  .
.
3. Grafické riešenie rovníc a nerovníc s modulom
Riešenie rovníc so znamienkom absolútnej hodnoty je často oveľa pohodlnejšie riešiť nie analyticky, ale graficky (najmä rovnice obsahujúce parametre).
Príklad 9(C5, jednotná štátna skúška – 2010)
C5. Pre každú hodnotua
uveďte počet riešení rovnice 
Riešenie.Nakreslíme funkciu
 ... Ak to chcete urobiť, vyberte celý štvorec:
... Ak to chcete urobiť, vyberte celý štvorec:
Počet priesečníkov grafu funkcie y =  s vodorovnými čiarami y = a sa rovná počtu riešení rovnice.
s vodorovnými čiarami y = a sa rovná počtu riešení rovnice.
O  odpoveď:
ak
odpoveď:
ak  < 0, то решений нет; если а= 0, то два решения, если
< 0, то решений нет; если а= 0, то два решения, если  0 < а < 4, то четыре решения; если а=4, то три решения; если а >4, potom dve riešenia.
0 < а < 4, то четыре решения; если а=4, то три решения; если а >4, potom dve riešenia.
Iné spôsoby riešenia rovníc a nerovníc s modulom
Spôsob rozšírenia modulu
Uvažujme o spôsobe rozšírenia modulov na príklade:
Príklad 10 Vyriešte rovnicu
Riešenie. Táto rovnica obsahuje viac ako jeden modul.
Metóda riešenia rovníc obsahujúcich premenné pod znamienkom dvoch alebo viacerých modulov je nasledovná.
1. Nájdite hodnoty premennej, pri ktorej každý z modulov zmizne: 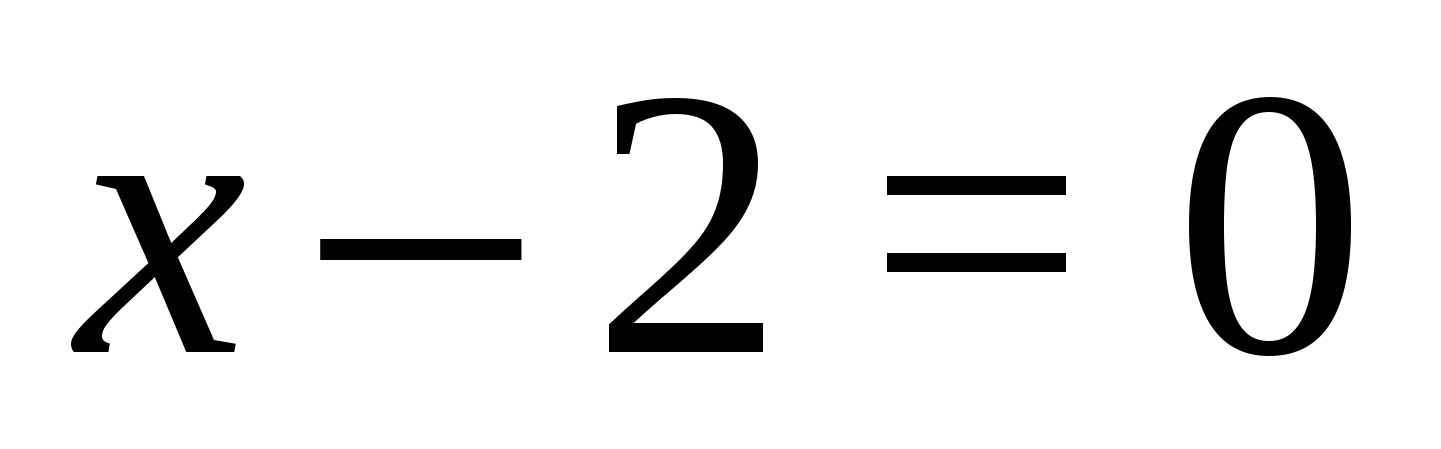 ,
,  ;
;  ,
,  ;
;  ,
,  .
.
2. Označte tieto body na číselnej osi.
3. Zvážte rovnicu v každom z intervalov a nastavte znamienko výrazov, ktoré sú pod modulmi.
1) Kedy  alebo
alebo  ... Na určenie znamienka každého z výrazov pod modulom v tomto intervale stačí vziať ľubovoľnú hodnotu
... Na určenie znamienka každého z výrazov pod modulom v tomto intervale stačí vziať ľubovoľnú hodnotu  z tohto intervalu a nahradiť vo výraze. Ak je získaná hodnota záporná, potom pre všetkých
z tohto intervalu a nahradiť vo výraze. Ak je získaná hodnota záporná, potom pre všetkých  od tohto intervalu bude výraz záporný; ak je získaná číselná hodnota kladná, tak pre všetky hodnoty
od tohto intervalu bude výraz záporný; ak je získaná číselná hodnota kladná, tak pre všetky hodnoty  od tohto intervalu bude výraz kladný.
od tohto intervalu bude výraz kladný.
Zoberme si význam  mimo
mimo  a dosaďte jeho hodnotu do výrazu
a dosaďte jeho hodnotu do výrazu 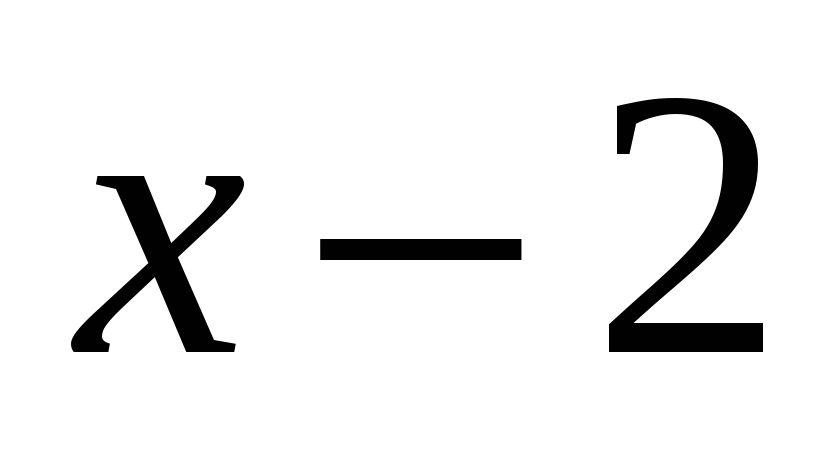 , dostaneme
, dostaneme  , teda v tomto intervale
, teda v tomto intervale 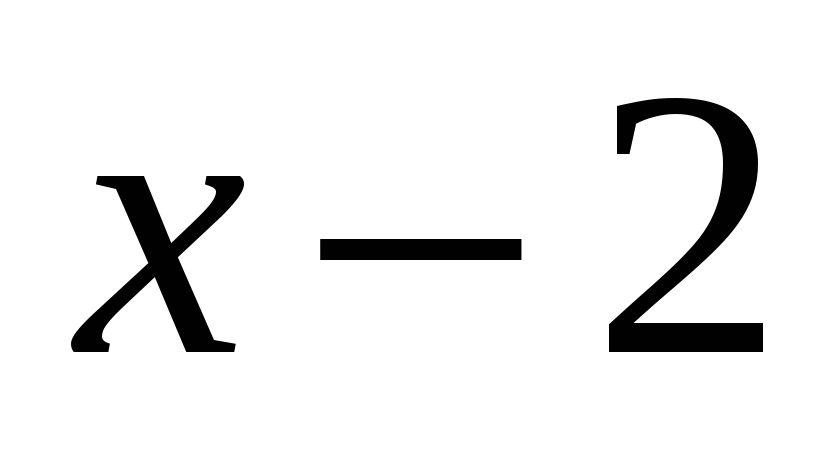 záporné, a preto `` vyjde '' spod modulu so znamienkom mínus, dostaneme:
záporné, a preto `` vyjde '' spod modulu so znamienkom mínus, dostaneme: 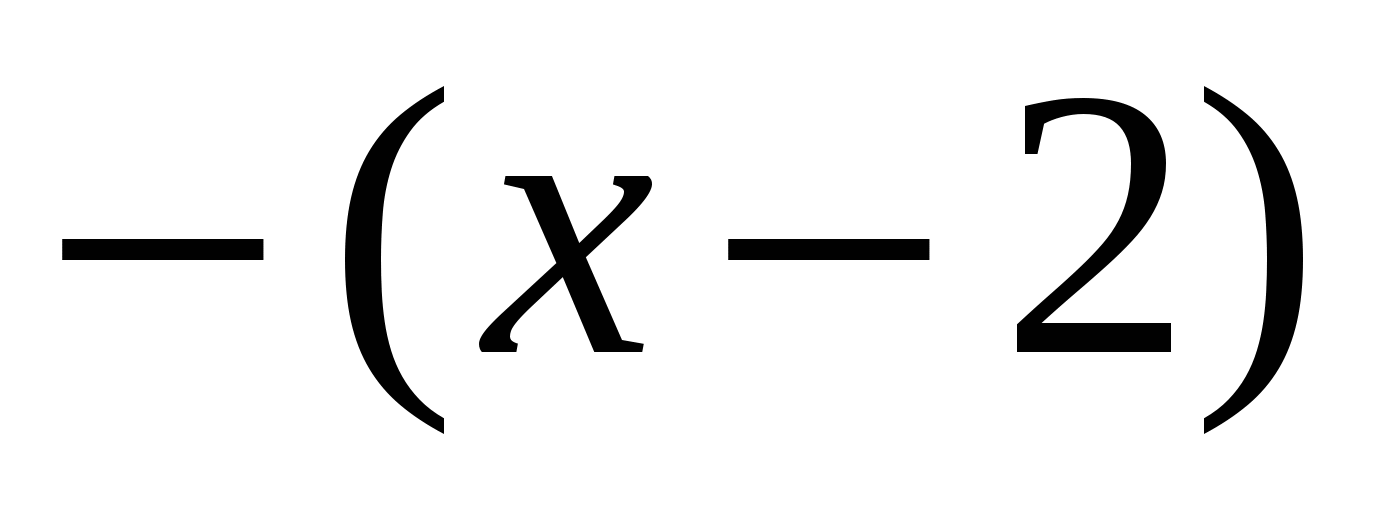 .
.
S touto hodnotou  , výraz
, výraz  dostane zmysel
dostane zmysel 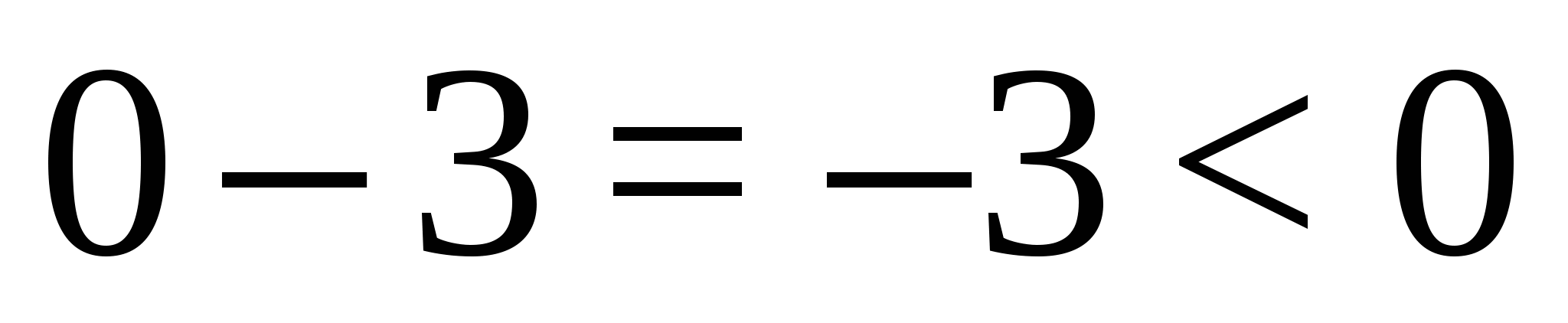 , čo znamená, že je v intervale
, čo znamená, že je v intervale  nadobúda aj záporné hodnoty a modul opustí so znamienkom mínus, dostaneme:
nadobúda aj záporné hodnoty a modul opustí so znamienkom mínus, dostaneme:  .
.
Výraz 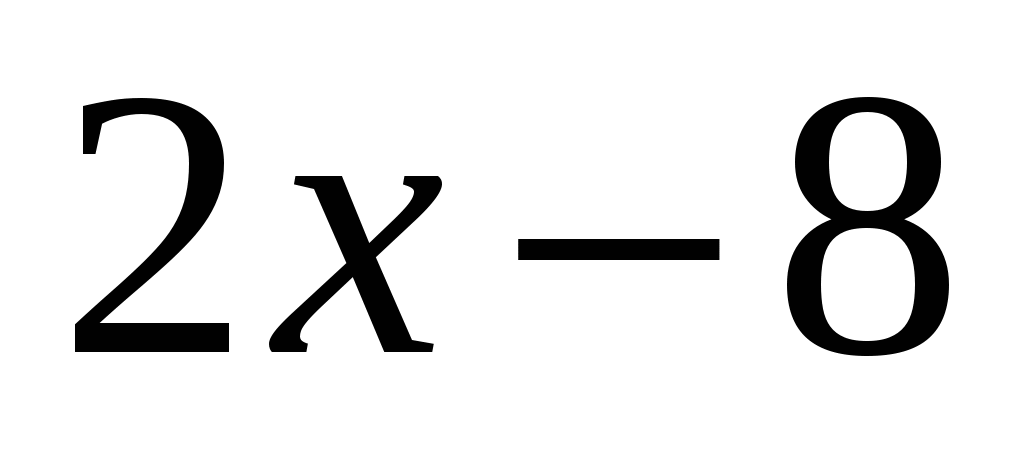 dostane zmysel
dostane zmysel  a "opustiť" spod modulu so znamienkom mínus ":
a "opustiť" spod modulu so znamienkom mínus ":  .
.
Rovnica na tomto intervale dopadne takto: keď ju vyriešime, nájdeme:  .
.
Zisťujeme, či je táto hodnota zahrnutá v intervale  ... Ukazuje sa, že je zahrnutý, čo znamená
... Ukazuje sa, že je zahrnutý, čo znamená  je koreňom rovnice.
je koreňom rovnice.
2) Kedy  ... Vyberieme ľubovoľnú hodnotu
... Vyberieme ľubovoľnú hodnotu  z tejto medzery. Nechať byť
z tejto medzery. Nechať byť 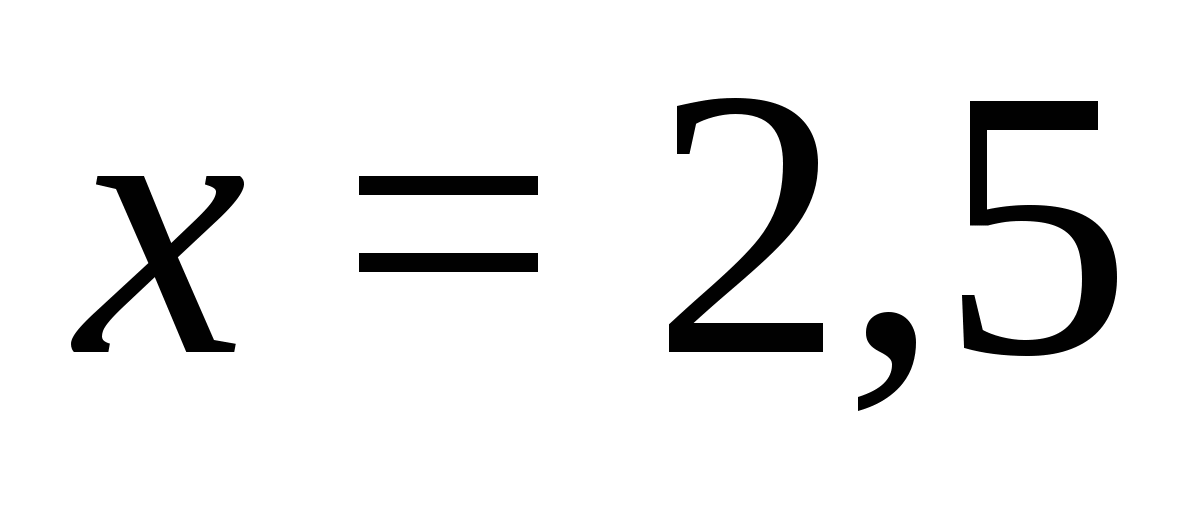 ... Určite znamienko každého z výrazov pod modulom pri tejto hodnote
... Určite znamienko každého z výrazov pod modulom pri tejto hodnote  ... Ukazuje sa, že výraz
... Ukazuje sa, že výraz 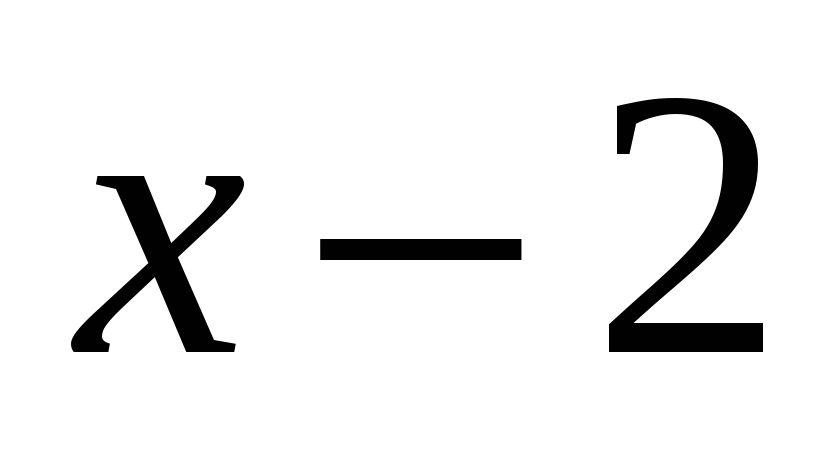 je pozitívny a ďalšie dva sú negatívne.
je pozitívny a ďalšie dva sú negatívne.
Rovnica na tomto intervale bude mať tvar:. Keď to vyriešime, nájdeme  ... Táto hodnota nie je zahrnutá v rozsahu
... Táto hodnota nie je zahrnutá v rozsahu 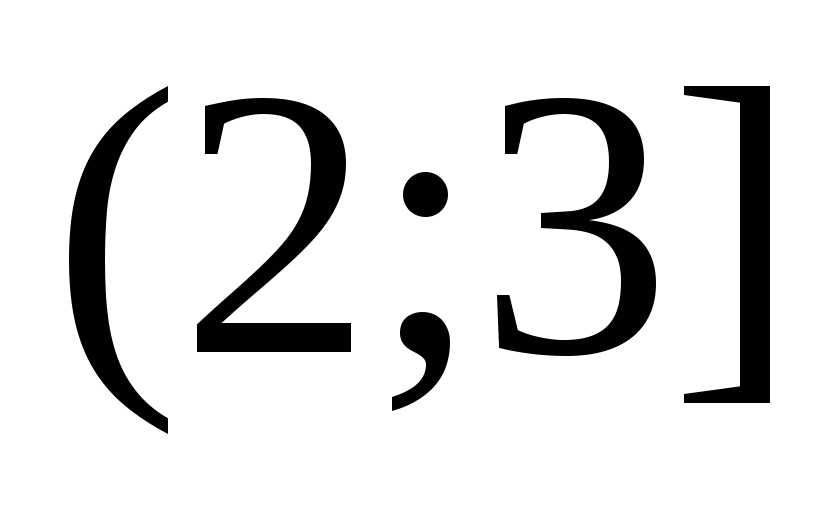 , čo znamená, že to nie je koreň rovnice.
, čo znamená, že to nie je koreň rovnice.
3) Kedy 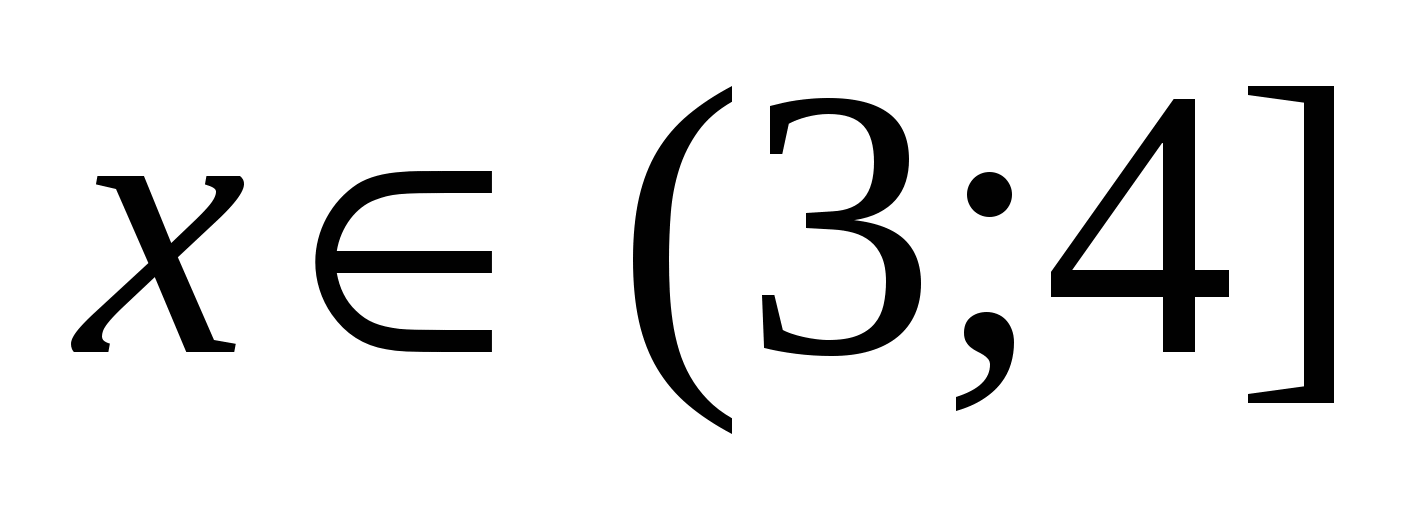 ... Výber ľubovoľnej hodnoty
... Výber ľubovoľnej hodnoty  z tohto intervalu, povedzme
z tohto intervalu, povedzme  a nahradiť v každom z výrazov. Zisťujeme, že výrazy
a nahradiť v každom z výrazov. Zisťujeme, že výrazy 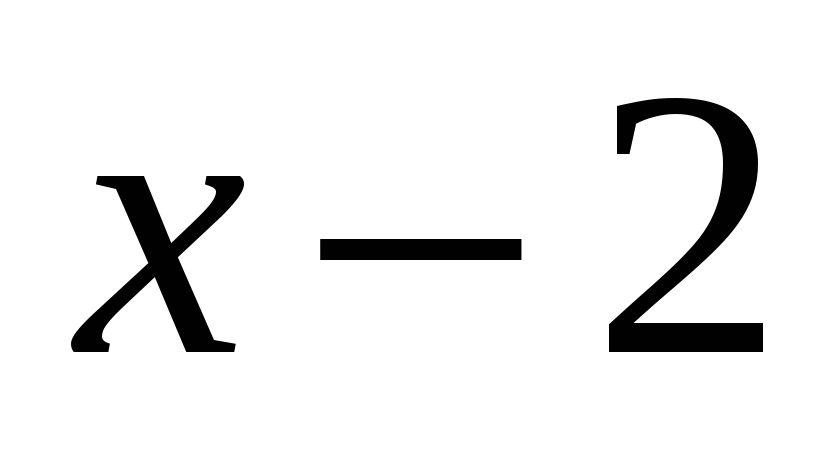 a
a  sú pozitívne a
sú pozitívne a 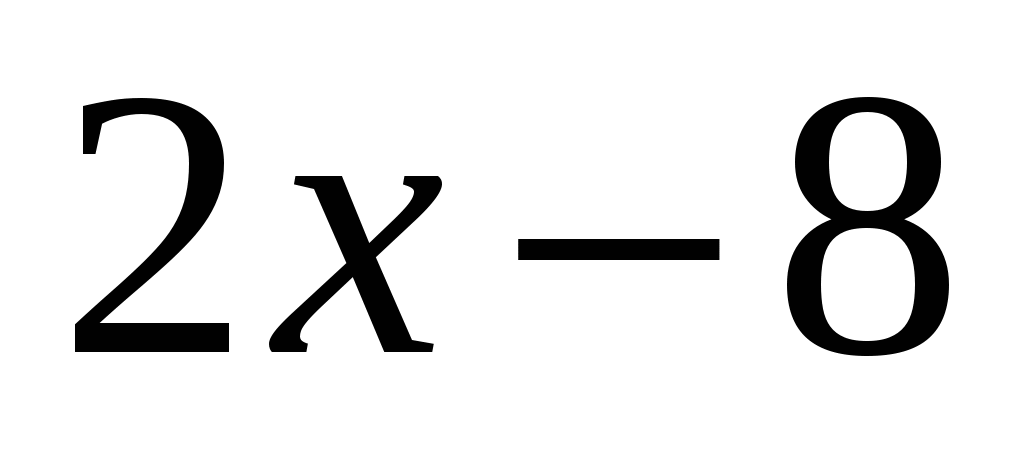 - negatívny. Dostaneme nasledujúcu rovnicu:.
- negatívny. Dostaneme nasledujúcu rovnicu:.
Po transformácii dostaneme:  , čo znamená, že rovnica nemá korene v tomto intervale.
, čo znamená, že rovnica nemá korene v tomto intervale.
4) Kedy  ... Je ľahké zistiť, že všetky výrazy v tomto intervale sú kladné, čo znamená, že dostaneme rovnicu:,
... Je ľahké zistiť, že všetky výrazy v tomto intervale sú kladné, čo znamená, že dostaneme rovnicu:,  ,
,  ktorý je zahrnutý v intervale a je koreňom rovnice.
ktorý je zahrnutý v intervale a je koreňom rovnice.
Odpoveď.  ,
,  .
.
Riešenie rovníc obsahujúcich moduly nezáporných výrazov
Príklad 11 Aký je súčet koreňov rovnice (koreň, ak je jeden) rovnice

Riešenie. Zvážte výraz
 a transformovať ho do formy
a transformovať ho do formy 
Je zrejmé, že čitateľ zlomku je kladné číslo pre akúkoľvek hodnotu premennej. Zlomkový výraz znamená kladné, ak  (od r
(od r  ). Výsledný výraz transformujeme za predpokladu
). Výsledný výraz transformujeme za predpokladu  ... Dostaneme rovnicu ekvivalentnú tej pôvodnej:
... Dostaneme rovnicu ekvivalentnú tej pôvodnej:

Odpoveď.  .
.
Príklad 12 Vyriešte rovnicu

Riešenie. Keďže ľavá strana rovnice je nezáporná, pre všetky prípustné hodnoty premennej, na množine koreňov rovnice musí byť nezáporná aj jej pravá strana, teda podmienka  , na tomto intervale sú menovatele oboch zlomkov rovnaké a zostáva vyriešiť rovnicu
, na tomto intervale sú menovatele oboch zlomkov rovnaké a zostáva vyriešiť rovnicu  ... Riešiť to a zvážiť obmedzenie
... Riešiť to a zvážiť obmedzenie  , dostaneme
, dostaneme
Odpoveď.  .
.
Riešenie rovníc pomocou geometrickej interpretácie
Geometrický význam výrazu 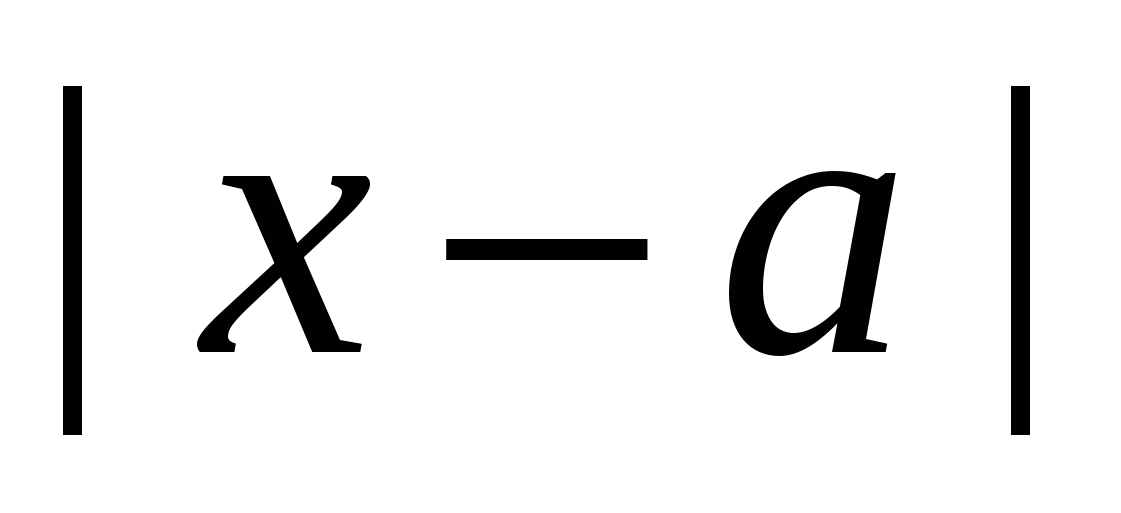 - dĺžka segmentu súradnicovej osi spájajúcej body s úsečkami
- dĺžka segmentu súradnicovej osi spájajúcej body s úsečkami  a
a  ... Preklad algebraického problému do geometrického jazyka sa často vyhýba ťažkopádnym výpočtom.
... Preklad algebraického problému do geometrického jazyka sa často vyhýba ťažkopádnym výpočtom.
Príklad 13 Poďme vyriešiť rovnicu  .
.
Riešenie. Budeme argumentovať nasledovne: na základe geometrickej interpretácie modulu je ľavá strana rovnice súčtom vzdialeností od nejakého bodu s úsečkou  až dva pevné body s úsečkami 1 a 2. Potom všetky body s úsečkami zo segmentu
až dva pevné body s úsečkami 1 a 2. Potom všetky body s úsečkami zo segmentu  majú požadovanú vlastnosť, ale body nachádzajúce sa mimo tohto segmentu nie.
majú požadovanú vlastnosť, ale body nachádzajúce sa mimo tohto segmentu nie.
Odpoveď.  .
.
Príklad 14 Vyriešte nerovnosť  .
.
Riešenie. Nakreslíme body na súradnicovej čiare, súčet vzdialeností, z ktorých k bodom  a
a  sa presne rovná
sa presne rovná  ... To všetko sú body segmentu
... To všetko sú body segmentu 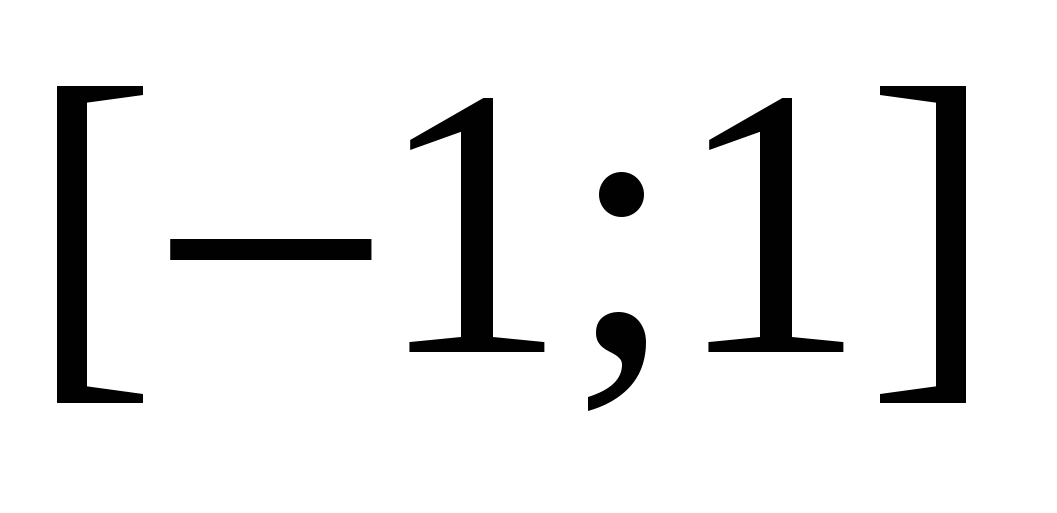 ... Pre všetky čísla mimo tohto segmentu bude súčet vzdialeností väčší ako dva.
... Pre všetky čísla mimo tohto segmentu bude súčet vzdialeností väčší ako dva.
Odpoveď. 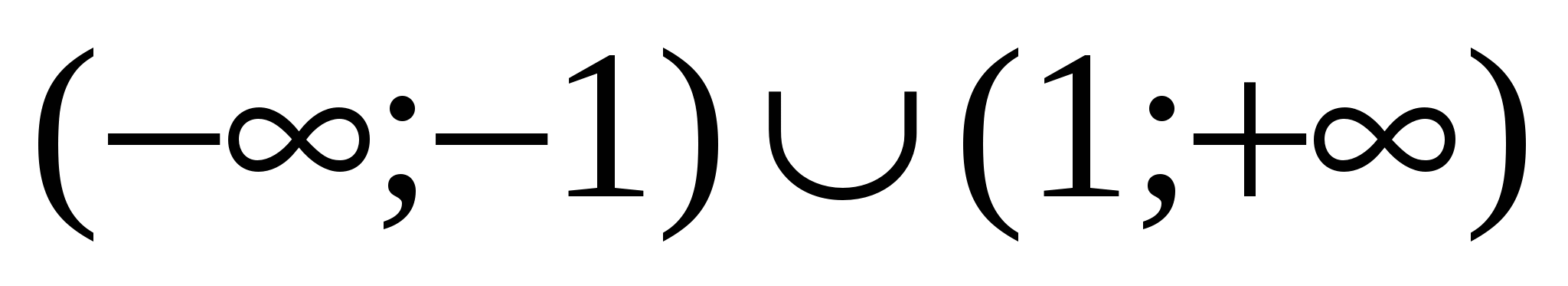 .
.
Príklad(C3, jednotná štátna skúška – 2010) 15 Vyriešte rovnicu

Riešenie. Aplikovanie identity dvakrát 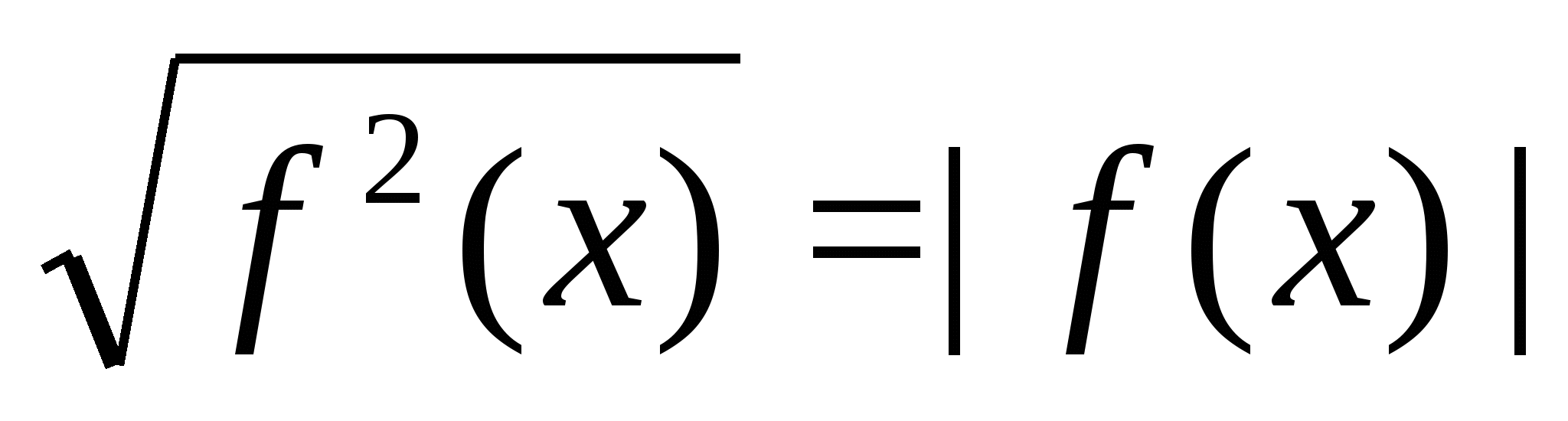 , dostaneme rovnicu
, dostaneme rovnicu

ktorého riešením je interval  .
.
Odpoveď.  .
.
Príklad(C3, jednotná štátna skúška – 2011) 16 17 Vyriešte rovnicu
Riešenie. .
Odpoveď.  .
.
Aplikácia znamienkovej vety na riešenie rovníc
Sformulujme vetu vhodnú na riešenie nerovníc vzhľadom na súčin alebo čiastkové rozdiely modulov:
Veta 18 Znamienko rozdielu medzi absolútnymi hodnotami týchto dvoch výrazov sa zhoduje so znamienkom rozdielu medzi štvorcami týchto výrazov.
nezmizne pre žiadnu hodnotu premennej. To znamená, že funkcia je znamienkovo konštantná v celej doméne definície. Výpočet napr.  , dostaneme, že funkcia nadobúda iba kladné hodnoty.
, dostaneme, že funkcia nadobúda iba kladné hodnoty.
Odpoveď.  .
.
Intervalová metóda umožňuje riešiť zložitejšie rovnice a nerovnice s modulmi, no v tomto prípade má trochu iný účel. Podstata je nasledovná. Nájdeme korene všetkých submodulárnych výrazov a rozdelíme číselnú os na intervaly stálosti týchto výrazov. To umožňuje pri postupnom prehliadaní týchto intervalov sa súčasne zbaviť všetkých modulov a vyriešiť obvyklú rovnicu alebo nerovnicu (pri kontrole, či je nájdená odpoveď zahrnutá v danom intervale).
Riešenie rovníc násobením kladným faktorom
Záver.
Ak zhrnieme našu prácu, môžeme povedať nasledovné.
Cieľom práce bolo študovať rôzne metódy riešenia rovníc a nerovníc s modulmi.
Uvažuje sa o niektorých variantoch najjednoduchších rovníc a nerovníc s modulom, vyriešených pomocou ekvivalentných prechodov, ako aj vety o súčte modulov; grafický spôsob riešenia rovníc. Treba povedať, že v kurze školskej matematiky sa práve tieto metódy riešenia využívajú najčastejšie. Pri riešení problémov je obzvlášť dôležitá grafická metóda C 5 z kontrolných a meracích materiálov skúšky.
Ďalej sme na niekoľkých príkladoch študovali iné spôsoby riešenia rovníc a nerovníc s modulmi, a to: metódu rozširovania modulov; riešenie rovníc obsahujúcich moduly nezáporných výrazov; riešenie rovníc pomocou geometrickej interpretácie; pomocou identity 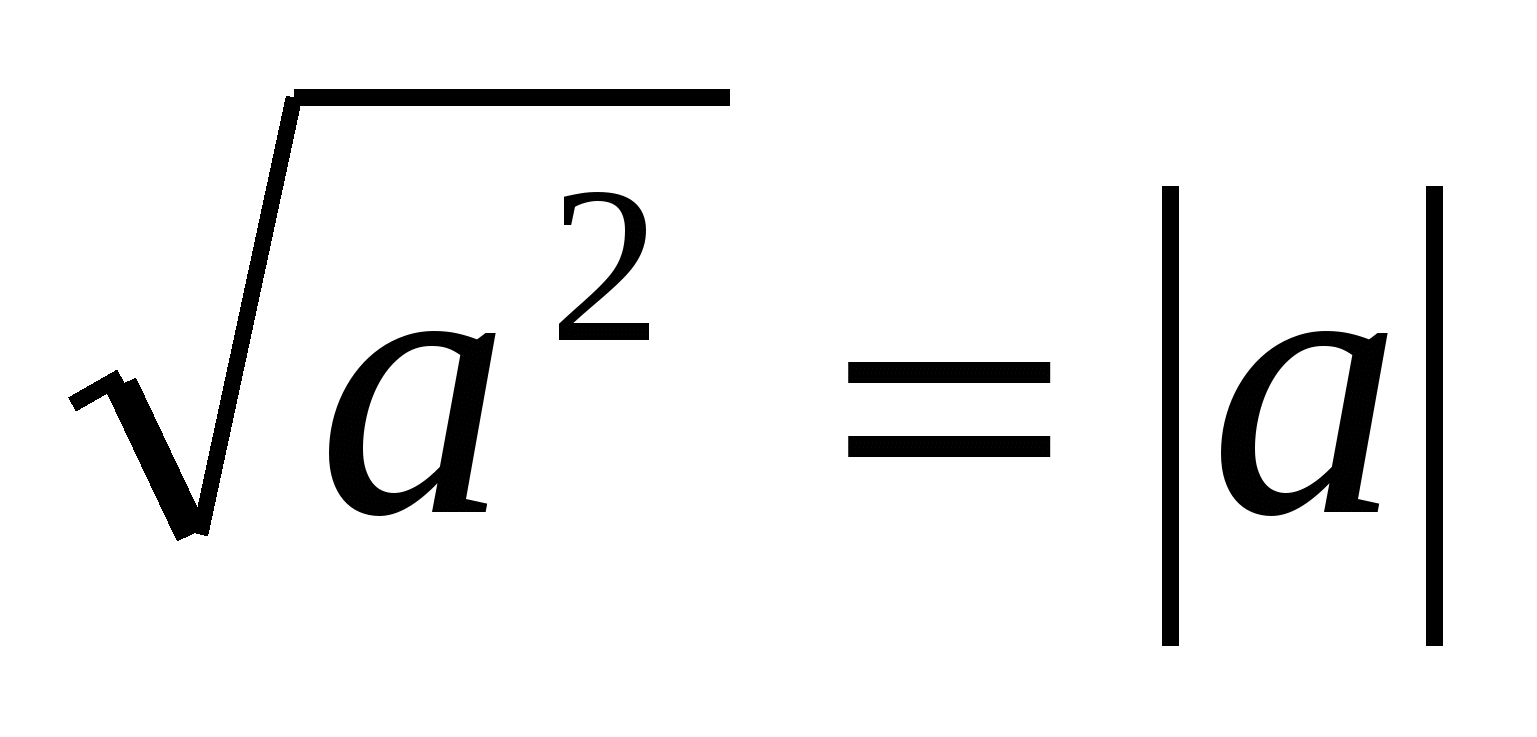 ; aplikácia znakovej vety; riešenie rovníc prechodom na dôsledok, násobenie kladným faktorom, ako aj riešenie nerovníc metódou intervalov.
; aplikácia znakovej vety; riešenie rovníc prechodom na dôsledok, násobenie kladným faktorom, ako aj riešenie nerovníc metódou intervalov.
V priebehu štúdie sme teda dospeli k nasledujúcim záverom.
Za najuniverzálnejšie a použiteľné na najväčší počet úloh považujeme metódu rozšírenia modulov, grafickú metódu a intervalovú metódu. Toto presvedčenie vzniklo ako dôsledok riešenia veľkého množstva problémov z kontrolných a meracích materiálov skúšky, predmetových majstrovstiev, olympiádových problémov, ako aj študovaním literatúry o tejto problematike. Za veľmi dôležité považujeme aj znalosť a aplikáciu identity. 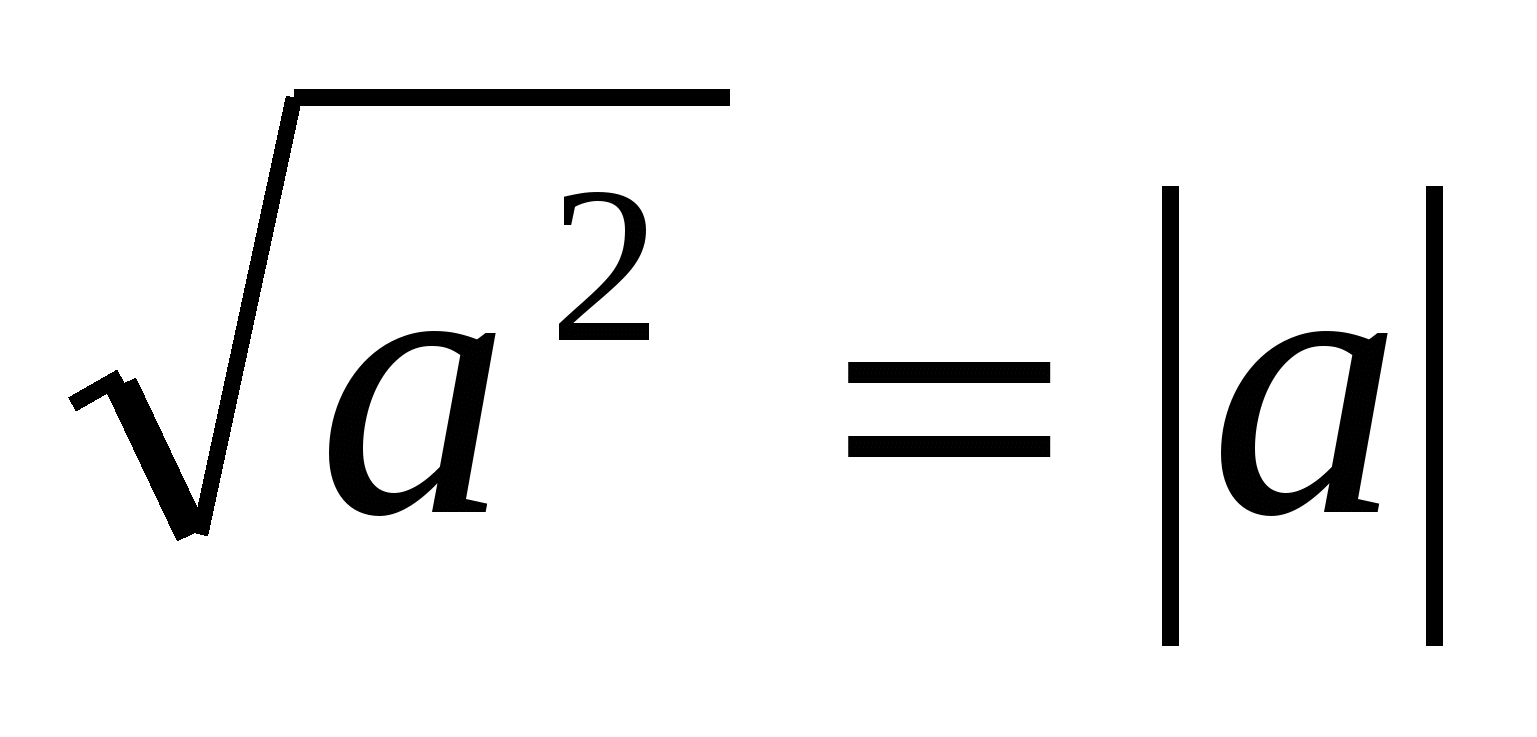 , keďže sa používa nielen na riešenie rovníc a nerovníc, ale aj na transformáciu mnohých výrazov s radikálmi. Ostatné metódy riešenia, o ktorých sme uvažovali, sú samozrejme veľmi zaujímavé z hľadiska rozšírenia matematických obzorov a všeobecného matematického rozvoja. Preto ich plánujeme využiť na prípravu na štátnu záverečnú certifikáciu formou Jednotnej štátnej skúšky a prípravu na štúdium na vysokej škole.
, keďže sa používa nielen na riešenie rovníc a nerovníc, ale aj na transformáciu mnohých výrazov s radikálmi. Ostatné metódy riešenia, o ktorých sme uvažovali, sú samozrejme veľmi zaujímavé z hľadiska rozšírenia matematických obzorov a všeobecného matematického rozvoja. Preto ich plánujeme využiť na prípravu na štátnu záverečnú certifikáciu formou Jednotnej štátnej skúšky a prípravu na štúdium na vysokej škole.
Bibliografia.
"Veľká matematická encyklopédia" pre školákov a študentov;
Matematika. Jednotná štátna skúška - 2011, 2012. Typické možnosti skúšky. / Editoval A.L. Semenová, I.V. Jaščenko.
M. Ya. Vygodsky. Referenčná príručka elementárnej matematiky
"Najnovšia príručka pre školákov";
Encyklopédia „Poznávam svet. Matematika";
;
Podľa modulu čísla volá sa samotné toto číslo, ak je nezáporné, alebo rovnaké číslo s opačným znamienkom, ak je záporné.
Napríklad modul čísla 6 je 6, modul čísla -6 je tiež 6.
To znamená, že absolútna hodnota čísla sa chápe ako absolútna hodnota, absolútna hodnota tohto čísla bez ohľadu na jeho znamienko.
Označuje sa takto: | 6 |, | NS|, |a| atď.
(Ďalšie podrobnosti nájdete v časti „Číselný modul“).
Rovnice s modulom.
Príklad 1 ... Vyriešte rovnicu|10 NS - 5| = 15.
Riešenie.
Podľa pravidla je rovnica ekvivalentná kombinácii dvoch rovníc:
10NS - 5 = 15
10NS - 5 = -15
Rozhodujeme sa:
10NS = 15 + 5 = 20
10NS = -15 + 5 = -10
NS = 20: 10
NS = -10: 10
NS = 2
NS = -1
Odpoveď: NS 1 = 2, NS 2 = -1.
Príklad 2 ... Vyriešte rovnicu|2 NS + 1| = NS + 2.
Riešenie.
Pretože modul je nezáporné číslo, potom NS+ 2 ≥ 0. Podľa toho:
NS ≥ -2.
Zostavíme dve rovnice:
2NS + 1 = NS + 2
2NS + 1 = -(NS + 2)
Rozhodujeme sa:
2NS + 1 = NS + 2
2NS + 1 = -NS - 2
2NS - NS = 2 - 1
2NS + NS = -2 - 1
NS = 1
NS = -1
Obidve čísla sú väčšie ako -2. Oboje sú teda koreňmi rovnice.
Odpoveď: NS 1 = -1, NS 2 = 1.
Príklad 3
... Vyriešte rovnicu
|NS + 3| - 1
————— = 4
NS - 1
Riešenie.
Rovnica dáva zmysel, ak menovateľ nie je nula – to znamená, ak NS≠ 1. Berme túto podmienku do úvahy. Naša prvá akcia je jednoduchá – zlomku sa nielen zbavíme, ale transformujeme ho tak, aby sme dostali modul v jeho čistej forme:
|NS+ 3 | - 1 = 4 ( NS - 1),
|NS + 3| - 1 = 4NS - 4,
|NS + 3| = 4NS - 4 + 1,
|NS + 3| = 4NS - 3.
Teraz máme iba výraz pod modulom na ľavej strane rovnice. Pohni sa.
Modul čísla je nezáporné číslo – to znamená, že musí byť väčší alebo rovný nule. Podľa toho riešime nerovnosť:
4NS - 3 ≥ 0
4NS ≥ 3
NS ≥ 3/4
Máme teda druhú podmienku: koreň rovnice musí byť aspoň 3/4.
V súlade s pravidlom zostavíme sadu dvoch rovníc a vyriešime ich:
NS + 3 = 4NS - 3
NS + 3 = -(4NS - 3)
NS + 3 = 4NS - 3
NS + 3 = -4NS + 3
NS - 4NS = -3 - 3
NS + 4NS = 3 - 3
NS = 2
NS = 0
Dostali sme dve odpovede. Skontrolujeme, či sú koreňmi pôvodnej rovnice.
Mali sme dve podmienky: koreň rovnice nemôže byť rovný 1 a musí byť aspoň 3/4. Teda NS ≠ 1, NS≥ 3/4. Obe tieto podmienky spĺňa iba jedna z dvoch prijatých odpovedí – číslo 2. To znamená, že iba ona je koreňom pôvodnej rovnice.
Odpoveď: NS = 2.
Nerovnosti s modulom.
Príklad 1 ... Vyriešte nerovnosť| NS - 3| < 4
Riešenie.
Pravidlo modulu hovorí:
|a| = a, ak a ≥ 0.
|a| = -a, ak a < 0.
Modul môže mať nezáporné aj záporné čísla. Preto musíme zvážiť oba prípady: NS- 3 ≥ 0 a NS - 3 < 0.
1) Kedy NS- 3 ≥ 0 naša pôvodná nerovnosť zostáva taká, aká je, len bez znamienka modulu:
NS - 3 < 4.
2) Kedy NS - 3 < 0 в исходном неравенстве надо поставить знак минус перед всем подмодульным выражением:
-(NS - 3) < 4.
Rozbalením zátvoriek dostaneme:
-NS + 3 < 4.
Z týchto dvoch podmienok sme sa dostali k spojeniu dvoch systémov nerovností:
NS - 3 ≥ 0
NS - 3 < 4
NS - 3 < 0
-NS + 3 < 4
Poďme ich vyriešiť:
NS ≥ 3
NS < 7
NS < 3
NS > -1
Takže v našej odpovedi máme spojenie dvoch množín:
3 ≤ NS < 7 U -1 < NS < 3.
Určte najmenšiu a najväčšiu hodnotu. Sú to -1 a 7. Súčasne NS väčší ako -1, ale menší ako 7.
okrem toho NS≥ 3. Riešením nerovnosti je teda celá množina čísel od -1 do 7, s výnimkou týchto extrémnych čísel.
Odpoveď: -1 < NS < 7.
alebo: NS ∈ (-1; 7).
Doplnky.
1) Na vyriešenie našej nerovnosti existuje jednoduchší a kratší spôsob – grafický. K tomu je potrebné nakresliť vodorovnú os (obr. 1).
Výraz | NS - 3| < 4 означает, что расстояние от точки NS k bodu 3 je menej ako štyri jednotky. Na osi označíme číslo 3 a napočítame 4 dieliky naľavo a napravo od neho. Vľavo prídeme k bodu -1, vpravo - k bodu 7. Teda body NS len sme videli bez toho, aby sme ich vypočítali.
Navyše, podľa podmienky nerovnosti, samotné -1 a 7 nie sú zahrnuté v množine riešení. Dostávame teda odpoveď:
1 < NS < 7.
2) Je tu ale ešte jedno riešenie, ktoré je jednoduchšie aj graficky. Aby sme to dosiahli, naša nerovnosť musí byť reprezentovaná v tejto forme:
4 < NS - 3 < 4.
Veď takto je to podľa modulového pravidla. Nezáporné číslo 4 a podobné záporné číslo -4 sú hranice na vyriešenie nerovnosti.
4 + 3 < NS < 4 + 3
1 < NS < 7.
Príklad 2 ... Vyriešte nerovnosť| NS - 2| ≥ 5
Riešenie.
Tento príklad sa výrazne líši od predchádzajúceho. Ľavá strana je väčšia ako 5 alebo rovná 5. Z geometrického hľadiska sú riešením nerovnosti všetky čísla, ktoré sú od bodu 2 vo vzdialenosti 5 jednotiek a viac (obr. 2). Z grafu vyplýva, že sú to všetky čísla, ktoré sú menšie alebo rovné -3 a väčšie alebo rovné 7. Takže odpoveď sme už dostali.
Odpoveď: -3 ≥ NS ≥ 7.
Popri tom tú istú nerovnosť riešime permutovaním voľného termínu doľava a doprava s opačným znamienkom:
5 ≥ NS - 2 ≥ 5
5 + 2 ≥ NS ≥ 5 + 2
Odpoveď je rovnaká: -3 ≥ NS ≥ 7.
alebo: NS ∈ [-3; 7]
Príklad vyriešený.
Príklad 3 ... Vyriešte nerovnosť 6 NS 2 - | NS| - 2 ≤ 0
Riešenie.
číslo NS môže byť kladný, záporný alebo nulový. Preto musíme brať do úvahy všetky tri okolnosti. Ako viete, berú sa do úvahy v dvoch nerovnostiach: NS≥ 0 a NS < 0. При NS≥ 0 len prepíšeme našu pôvodnú nerovnosť tak, ako je, len bez znamienka modulu:
6x 2 - NS - 2 ≤ 0.
Teraz o druhom prípade: ak NS < 0. Модулем отрицательного числа является это же число с противоположным знаком. То есть пишем число под модулем с обратным знаком и опять же освобождаемся от знака модуля:
6NS 2 - (-NS) - 2 ≤ 0.
Rozbaľte zátvorky:
6NS 2 + NS - 2 ≤ 0.
Dostali sme teda dva systémy rovníc:
6NS 2 - NS - 2 ≤ 0
NS ≥ 0
6NS 2 + NS - 2 ≤ 0
NS < 0
Je potrebné riešiť nerovnice v systémoch - čo znamená, že je potrebné nájsť korene dvoch kvadratických rovníc. Aby sme to dosiahli, vyrovnáme ľavé strany nerovností k nule.
Začnime prvým:
6NS 2 - NS - 2 = 0.
Ako sa rieši kvadratická rovnica - pozri časť "Kvadratická rovnica". Odpoveď hneď pomenujeme:
NS 1 = -1/2, x 2 = 2/3.
Z prvej sústavy nerovníc zistíme, že riešením pôvodnej nerovnosti je celá množina čísel od -1/2 do 2/3. Píšeme spojenie riešení pre NS ≥ 0:
[-1/2; 2/3].
Teraz vyriešme druhú kvadratickú rovnicu:
6NS 2 + NS - 2 = 0.
Jeho korene:
NS 1 = -2/3, NS 2 = 1/2.
Záver: o hod NS < 0 корнями исходного неравенства являются также все числа от -2/3 до 1/2.
Spojme dve odpovede a získame konečnú odpoveď: riešením je celá množina čísel od -2/3 do 2/3, vrátane týchto extrémnych čísel.
Odpoveď: -2/3 ≤ NS ≤ 2/3.
alebo: NS ∈ [-2/3; 2/3].
Tento článok je venovaný technikám riešenia rôznych rovníc a nerovníc obsahujúcich
premenná pod znakom modulu.
Ak na skúške narazíte na rovnicu alebo nerovnosť s modulom, môžete to vyriešiť pomocou
bez toho, aby ste poznali nejaké špeciálne metódy a používali len definíciu modulu. pravda,
môže to trvať hodinu a pol drahocenného času na skúšku.
Preto vám chceme povedať o technikách, ktoré zjednodušujú riešenie takýchto problémov.
V prvom rade si to zapamätajte
![]()
Zvážte rôzne typy rovnice s modulom... (K nerovnostiam prejdeme neskôr.)
Vľavo je modul, vpravo číslo
Toto je najjednoduchší prípad. Poďme vyriešiť rovnicu
Existujú iba dve čísla, ktorých moduly sa rovnajú štyrom. Sú to 4 a -4. Preto rovnica
je ekvivalentná kombinácii dvoch jednoduchých:
Druhá rovnica nemá riešenia. Riešenia prvého: x = 0 a x = 5.
Odpoveď: 0; 5.
Variabilné pod modulom aj mimo modulu
Tu musíte modul podľa definície rozšíriť. ... ... alebo myslite!
Rovnica sa delí na dva prípady v závislosti od znamienka výrazu pod modulom.
Inými slovami, ide o kombináciu dvoch systémov:
![]()
Riešenie prvého systému:. Druhý systém nemá riešenia.
odpoveď: 1.
Prvý prípad: x ≥ 3. Odstráňte modul:
Číslo, ktoré je záporné, nespĺňa podmienku x ≥ 3, a preto nie je koreňom pôvodnej rovnice.
Poďme zistiť, či číslo spĺňa túto podmienku. Za týmto účelom zostavte rozdiel a určite jeho znamienko:
Preto je viac ako tri, a preto je koreňom pôvodnej rovnice
Druhý prípad: x< 3. Снимаем модуль:
číslo . väčší ako, a preto nespĺňa podmienku x< 3. Проверим :
Znamená, . je koreň pôvodnej rovnice.
Odstrániť modul podľa definície? Je desivé čo i len pomyslieť, pretože diskriminant nie je úplný štvorec. Využime radšej nasledujúcu úvahu: rovnicu tvaru |A | = B je ekvivalentné kombinácii dvoch systémov:
![]()
To isté, ale trochu iné:
Inými slovami, riešime dve rovnice, A = B a A = −B, a potom vyberieme korene, ktoré spĺňajú podmienku B ≥ 0.
Začnime. Najprv vyriešime prvú rovnicu:
Potom vyriešime druhú rovnicu:
Teraz v každom prípade skontrolujeme znamienko pravej strany:
Preto len a sú vhodné.
Kvadratické rovnice s náhradou | x | = t
Poďme vyriešiť rovnicu:
Pretože je vhodné vykonať výmenu | x | = t. Dostaneme:
![]()
Odpoveď: ± 1.
Modul sa rovná modulu
Hovoríme o rovniciach tvaru |A | = | B |. Toto je dar osudu. Žiadne zverejnenie modulu podľa definície! Je to jednoduché:
Uvažujme napríklad rovnicu:. Je ekvivalentná nasledujúcemu agregátu:
Zostáva vyriešiť každú z rovníc množiny a zapísať odpoveď.
Dva alebo viac modulov
Poďme vyriešiť rovnicu:
Nebudeme sa vŕtať v každom module zvlášť a rozširovať ho podľa definície - možností bude priveľa. Existuje racionálnejší spôsob - metóda intervalov.
Modulové výrazy zanikajú v bodoch x = 1, x = 2 a x = 3. Tieto body rozdeľujú číselnú os na štyri intervaly (intervaly). Tieto body označíme na číselnej osi a znamienka pre každý z výrazov usporiadame pod moduly v získaných intervaloch. (Poradie znakov je rovnaké ako poradie zodpovedajúcich modulov v rovnici.)

Preto musíme zvážiť štyri prípady - keď x je v každom z intervalov.
Prípad 1: x ≥ 3. Všetky moduly sú odstránené „s plusom“:
Výsledná hodnota x = 5 spĺňa podmienku x ≥ 3 a je teda koreňom pôvodnej rovnice.
Prípad 2: 2 ≤ x ≤ 3. Posledný modul je teraz odstránený „s mínusom“:
Výsledná hodnota x je tiež dobrá - patrí do uvažovaného intervalu.
Prípad 3: 1 ≤ x ≤ 2. Druhý a tretí modul sa odstránia „s mínusom“:
Získali sme správnu číselnú rovnosť pre ľubovoľné x z uvažovaného intervalu, ktoré slúži ako riešenie tejto rovnice.
Prípad 4: x ≤ 1 ≤ 1. Druhý a tretí modul sa odstránia „s mínusom“:
Nič nové. Už vieme, že x = 1 je riešenie.
Odpoveď: ∪ (5).
Modul v module
Poďme vyriešiť rovnicu:
Začneme rozšírením interného modulu.
1) x ≤ 3. Dostaneme:
Výraz pod modulom mizne pri. Tento bod patrí k uvažovaným
interval. Preto musíme analyzovať dva podprípady.
1.1) V tomto prípade dostaneme:
Táto hodnota x nie je platná, pretože nepatrí do posudzovaného intervalu.
1.2). potom:
Táto hodnota x tiež nie je platná.
Takže pre x ≤ 3 neexistujú žiadne riešenia. Prejdime k druhému prípadu.
2) x ≥ 3. Máme:
Tu máme šťastie: výraz x + 2 je v uvažovanom intervale kladný! Preto už nebudú žiadne ďalšie podprípady: modul sa odstráni „s plusom“:
Táto hodnota x je v uvažovanom intervale, a preto je koreňom pôvodnej rovnice.
Takto sú vyriešené všetky úlohy tohto typu - postupne otvárame vnorené moduly, počnúc interným.
Matematika je symbolom múdrosti vedy,
model vedeckej prísnosti a jednoduchosti,
štandard dokonalosti a krásy vo vede.
Ruský filozof, profesor A.V. Vološinov
Nerovnosti modulov
Najťažšie riešiteľné problémy školskej matematiky sú nerovnosti, obsahujúce premenné pod znakom modulu. Na úspešné vyriešenie takýchto nerovností je potrebné dobre poznať vlastnosti modulu a mať zručnosti na ich používanie.
Základné pojmy a vlastnosti
Modul (absolútna hodnota) reálneho čísla označené a je definovaný takto:
Jednoduché vlastnosti modulu zahŕňajú nasledujúce pomery:
A .
Poznámka, že posledné dve vlastnosti platia pre ľubovoľný párny stupeň.
Navyše, ak, kde, tak
Zložitejšie vlastnosti modulu, ktoré možno efektívne použiť na riešenie rovníc a nerovníc s modulmi, sú formulované pomocou nasledujúcich teorém:
Veta 1.Pre akékoľvek analytické funkcie a nerovnosť je pravdivá.
Veta 2. Rovnosť rovná nerovnosti.
Veta 3. Rovnosť rovná nerovnosti.
Najčastejšie nerovnosti v školskej matematike, obsahujúce neznáme premenné pod znamienkom modulu, sú nerovnosti tvaru a kde nejaká pozitívna konštanta.
Veta 4. Nerovnosť je ekvivalentná dvojitej nerovnosti, a riešenie nerovnostisa redukuje na riešenie množiny nerovností a .
Táto veta je špeciálnym prípadom vety 6 a 7.
Zložitejšie nerovnosti, obsahujúce modul sú nerovnosti tvaru a .
Metódy riešenia takýchto nerovností možno formulovať pomocou nasledujúcich troch viet.
Veta 5. Nerovnosť je ekvivalentná kombinácii dvoch systémov nerovností
a (1)
Dôkaz. Odvtedy
To znamená platnosť (1).
Veta 6. Nerovnosť je ekvivalentom systému nerovností
Dôkaz. pretože , potom z nerovnosti z toho vyplýva ... Za tejto podmienky nerovnosťa v tomto prípade sa druhý systém nerovností (1) ukazuje ako nekonzistentný.
Veta je dokázaná.
Veta 7. Nerovnosť je ekvivalentné súhrnu jednej nerovnosti a dvoch systémov nerovností
a (3)
Dôkaz. Odvtedy nerovnosť vždy vykonaný, ak .
nechaj byť, potom nerovnosťbude ekvivalentná nerovnosti, z čoho vyplýva množina dvoch nerovností a .
Veta je dokázaná.
Pozrime sa na typické príklady riešenia problémov na tému „Nerovnosti, obsahujúce premenné pod znakom modulu ".
Riešenie nerovností modulom
Väčšina jednoduchá metóda riešenie nerovností s modulom je metóda, založené na rozširovaní modulov. Táto metóda je všestranná, vo všeobecnosti však môže jeho aplikácia viesť k veľmi ťažkopádnym výpočtom. Žiaci by preto mali poznať iné (efektívnejšie) metódy a techniky riešenia takýchto nerovností. Najmä, musíte mať zručnosti v uplatňovaní teorémov, uvedené v tomto článku.
Príklad 1Vyriešte nerovnosť
. (4)
Riešenie.Nerovnosť (4) bude riešená „klasickou“ metódou – metódou rozširovania modulov. Na tento účel sme rozdelili číselnú os bodov a do intervalov a zvážte tri prípady.
1. Ak teda,,, a nerovnosť (4) nadobúda tvar alebo .
Keďže sa tu uvažuje o tomto prípade, ide o riešenie nerovnosti (4).
2. Ak, potom z nerovnosti (4) dostaneme alebo ... Od priesečníka intervalov a je prázdny, potom na uvažovanom intervale neexistujú žiadne riešenia nerovnosti (4).
3. Ak, potom má tvar nerovnosť (4). alebo . To je zrejmé je tiež riešením nerovnosti (4).
Odpoveď: ,.
Príklad 2 Vyriešte nerovnosť.
Riešenie. Predpokladajme, že. pretože , potom daná nerovnosť nadobudne tvar alebo . Odvtedy a teda nasleduje alebo .
Avšak preto, resp.
Príklad 3 Vyriešte nerovnosť
. (5)
Riešenie. pretože , potom nerovnosť (5) je ekvivalentná nerovnostiam alebo . teda podľa vety 4, máme súbor nerovností a .
Odpoveď: ,.
Príklad 4.Vyriešte nerovnosť
. (6)
Riešenie. Označme. Potom z nerovnosti (6) získame nerovnosti,, alebo.
teda pomocou metódy rozstupov, dostaneme. pretože , potom tu máme systém nerovností
Riešením prvej nerovnosti sústavy (7) je spojenie dvoch intervalov a , a riešením druhej nerovnosti je dvojitá nerovnosť... To znamená, že riešením sústavy nerovníc (7) je spojenie dvoch intervalov a .
odpoveď: ,
Príklad 5.Vyriešte nerovnosť
. (8)
Riešenie. Nerovnosť (8) transformujeme takto:
Alebo .
Použitie metódy medzier, dostaneme riešenie nerovnosti (8).
Odpoveď: .
Poznámka. Ak dáme a do podmienky vety 5, tak dostaneme.
Príklad 6. Vyriešte nerovnosť
. (9)
Riešenie. Nerovnosť (9) znamená... Nerovnosť (9) transformujeme takto:
Alebo
Od vtedy resp.
Odpoveď: .
Príklad 7.Vyriešte nerovnosť
. (10)
Riešenie. Odkedy a, potom alebo.
V tomto smere a nerovnosť (10) nadobúda tvar
Alebo
. (11)
Z toho vyplýva, že resp. Keďže potom z nerovnosti (11) vyplýva aj resp.
Odpoveď: .
Poznámka. Ak použijeme vetu 1 na ľavú stranu nerovnosti (10), potom dostaneme ... Z toho a nerovnosti (10) vyplýva, že alebo. pretože , potom má tvar nerovnosť (10). alebo .
Príklad 8. Vyriešte nerovnosť
. (12)
Riešenie. Odvtedy a nerovnosť (12) implikuje alebo . Avšak preto, resp. Odtiaľto dostávame resp.
Odpoveď: .
Príklad 9. Vyriešte nerovnosť
. (13)
Riešenie. Podľa vety 7 je riešením nerovnice (13) alebo.
Nechaj teraz. V tomto prípade a nerovnosť (13) nadobúda tvar alebo .
Ak spojíte intervaly a , potom dostaneme riešenie nerovnosti (13) tvaru.
Príklad 10. Vyriešte nerovnosť
. (14)
Riešenie. Prepíšme nerovnosť (14) v ekvivalentnom tvare:. Ak aplikujeme vetu 1 na ľavú stranu tejto nerovnosti, dostaneme nerovnosť.
Z toho a z vety 1 vyplýva, že nerovnosť (14) platí pre akékoľvek hodnoty.
Odpoveď: ľubovoľné číslo.
Príklad 11. Vyriešte nerovnosť
. (15)
Riešenie. Použitie vety 1 na ľavú stranu nerovnosti (15), dostaneme ... Toto a nerovnosť (15) znamenajú rovnicu, ktorý má podobu.
Podľa vety 3, rovnica rovná nerovnosti... Z toho nám vychádza.
Príklad 12.Vyriešte nerovnosť
. (16)
Riešenie... Z nerovnosti (16) podľa vety 4 získame sústavu nerovností
Pri riešení nerovnostipoužijeme vetu 6 a získame systém nerovnícz čoho vyplýva.
Zvážte nerovnosť... Podľa vety 7, získame množinu nerovností a . Druhá populačná nerovnosť platí pre akúkoľvek realitu.
preto riešenie nerovnosti (16) je.
Príklad 13.Vyriešte nerovnosť
. (17)
Riešenie. Podľa vety 1 môžeme písať
(18)
Berúc do úvahy nerovnosť (17) usudzujeme, že obe nerovnosti (18) sa menia na rovnosť, t.j. systém rovníc platí
Podľa vety 3 tento systém rovníc je ekvivalentná sústave nerovníc
alebo
Príklad 14.Vyriešte nerovnosť
. (19)
Riešenie. Odvtedy. Obe strany nerovnosti (19) vynásobíme výrazom, ktorý pre akékoľvek hodnoty nadobúda iba kladné hodnoty. Potom dostaneme nerovnosť, ktorá je ekvivalentná nerovnosti (19) tvaru
Odtiaľto sa dostaneme alebo, kde. Keďže a, potom riešenie nerovnosti (19) je a .
Odpoveď: ,.
Pre hlbšie štúdium metód na riešenie nerovností pomocou modulu vám odporúčame použiť návody, uvedené v zozname odporúčanej literatúry.
1. Zbierka úloh z matematiky pre uchádzačov na technické vysoké školy / Ed. M.I. Skanavi. - M .: Mier a vzdelanie, 2013 .-- 608 s.
2. Suprun V.P. Matematika pre stredoškolákov: metódy riešenia a dokazovania nerovníc. - M .: Lenand / URSS, 2018 .-- 264 s.
3. Suprun V.P. Matematika pre stredoškolákov: neštandardné metódy riešenia problémov. - M .: CD "Librokom" / URSS, 2017 .-- 296 s.
Stále máte otázky?
Ak chcete získať pomoc od tútora - zaregistrujte sa.
stránky, s úplným alebo čiastočným kopírovaním materiálu, je potrebný odkaz na zdroj.