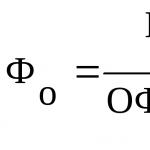При изучении какой-либо темы школьного курса можно отобрать определенный минимум задач, овладев методами решения которых, учащиеся будут в состоянии решить любую задачу на уровне программных требований по изучаемой теме. Предлагаю рассмотреть задачи, которые позволят увидеть взаимосвязи отдельных тем школьного курса математики. Поэтому составленная система задач является эффективным средством повторения, обобщения и систематизации учебного материала в ходе подготовки учащихся к экзамену.
Для сдачи экзамена не лишними будут дополнительные сведения о некоторых элементах треугольника. Рассмотрим свойства медианы треугольника и задачи, при решении которых этими свойствами можно воспользоваться. В предложенных задачах реализуется принцип уровневой дифференциации . Все задачи условно поделены на уровни (уровень указан в скобках после каждого задания).
Вспомним некоторые свойства медианы треугольника
Свойство 1. Докажите, что медиана треугольника ABC , проведённая из вершины A , меньше полусуммы сторон AB и AC .
Доказательство
https://pandia.ru/text/80/187/images/image002_245.gif" alt="$\displaystyle {\frac{AB + AC}{2}}$" width="90" height="60">.
Свойство 2. Медиана рассекает треугольник на два равновеликих.
Доказательство
Проведем из вершины B треугольника ABC медиану BD и высоту BE..gif" alt="Площадь" width="82" height="46">
Поскольку отрезок BD является медианой, то
что и требовалось доказать.
https://pandia.ru/text/80/187/images/image008_96.gif" alt="Медиана" align="left" width="196" height="75 src=">Свойство 4. Медианы треугольника делят треугольник на 6 равновеликих треугольников.
Доказательство
Докажем, что площадь каждого из шести треугольников, на которые медианы разбивают треугольник ABC, равна площади треугольника ABC. Для этого рассмотрим, например, треугольник AOF и опустим из вершины A перпендикуляр AK на прямую BF .
В силу свойства 2,
https://pandia.ru/text/80/187/images/image013_75.gif" alt="Медиана" align="left" width="105" height="132 src=">
Свойство 6. Медиана в прямоугольном треугольнике, проведённая из вершины прямого угла, равна половине гипотенузы.
Доказательство
https://pandia.ru/text/80/187/images/image015_62.gif" alt="Медиана" width="273" height="40 src="> что и требовалось доказать.
Следствия: 1. Центр описанной около прямоугольного треугольника окружности лежит на середине гипотенузы.
2. Если в треугольнике длина медианы равна половине длины стороны, к которой она проведена, то этот треугольник – прямоугольный.
ЗАДАЧИ
При решении каждой последующей задачи используются доказанные свойства.
№1 Темы: Удвоение медианы. Сложность: 2+
Признаки и свойства параллелограмма Классы: 8,9
Условие
На продолжении медианы AM треугольника ABC за точку M отложен отрезок MD , равный AM . Докажите, что четырёхугольник ABDC - параллелограмм.
Решение
Воспользуемся одним из признаков параллелограмма. Диагонали четырёхугольника ABDC пересекаются в точке M и делятся ею пополам, поэтому четырёхугольник ABDC - параллелограмм.
Медиана – это одна из основных линий треугольника. Этот отрезок и прямая, на которой он лежит, соединяет точку во главе угла треугольника с серединой противолежащей стороны этой же фигуры. В равностороннем треугольнике медиана является также биссектрисой и высотой.Свойство медианы, которое существенно облегчит решение многих задач, заключается в следующем: если в треугольнике провести медианы из каждого угла, то все они, пересекаясь в одной точке, будет делиться в соотношении 2:1. Соотношение следует отсчитывать от вершины угла.
Медиана имеет свойство разделять все поровну. Например, любая медиана делит треугольник на два других, равных по своей площади. А если провести все три медианы, то в большом треугольнике получится 6 маленьких, также равных по площади. Такие фигуры (с одинаковой площадью) называются равновеликими.
Биссектриса
Биссектриса представляет собой луч, который начинается в вершине угла и делит этот же угол пополам. Точки, лежащие на данном луче, равноудалены от сторон угла. Свойства биссектрисы хорошо помогают в решении задач, связанных с треугольниками.В треугольнике биссектрисой называют отрезок, который лежит на луче биссектрисы угла и соединяет вершину с противолежащей стороной. Точка пересечения со стороной делит ее на отрезки, отношение которых равно отношению прилежащих к ним сторонам.
Если в треугольник вписать окружность, то ее центр будет совпадать с точкой пересечения всех биссектрис данного треугольника. Это свойство имеет отражение и в стереометрии - там роль треугольника играет пирамида, а окружности - шар.
Высота
Также как медиана и биссектриса, высота в треугольнике в первую очередь связывают вершину угла и противолежащую сторону. Это связь проистекает в следующем: высота – это перпендикуляр, проведенный из вершины, к прямой, которая содержит в себе противолежащую сторону.Если высота проведена в прямоугольном треугольнике, то, касаясь противоположной стороны, она делит весь треугольник на два других, которые в свою очередь подобны первому.
Нередко понятие перпендикуляра применяется в стереометрии, чтобы определить взаиморасположения прямых в разных плоскостях и расстояние между ними. В этом случае отрезок, выполняющий функцию перпендикуляра, должен иметь прямой угол с обеими прямыми. Тогда числовое значение данного отрезка будет показывать расстояние между двумя фигурами.
Чтобы по сторонам треугольника найти медиану, не обязательно запоминать дополнительную формулу. Достаточно знать алгоритм решения.
Для начала рассмотрим задачу в общем виде.
Дан треугольник со сторонами a, b, c. Найти длину медианы, проведенной к стороне b.
AB=a, AC=b, BC=c.
На луче BF отложим отрезок FD, FD=BF.
Соединим точку D с точками A и C.
Четырехугольник ABCD — параллелограмм (по признаку), так как у него диагонали в точке пересечения делятся пополам.
Свойство диагоналей параллелограмма: сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.
Отсюда: AC²+BD²=2(AB²+BC²), значит, b²+BD²=2(a²+c²),
BD²=2(a²+c²)-b². По построению, BF — половина BD, следовательно,
Это — формула нахождения медианы треугольника по его сторонам. Обычно ее записывают так:
Переходим к рассмотрению конкретной задачи.
Стороны треугольника равны 13 см, 14 см и 15 см. Найти медиану треугольника, проведенную к его средней по длине стороне.
Применяя аналогичные рассуждения, получаем:
AC²+BD²=2(AB²+BC²).
14²+BD²=2(13²+15²)
Свойства
- Медианы треугольника пересекаются в одной точке , которая называется центроидом , и делятся этой точкой на две части в отношении 2:1, считая от вершины.
- Треугольник делится тремя медианами на шесть равновеликих треугольников.
- Большей стороне треугольника соответствует меньшая медиана.
- Из векторов, образующих медианы, можно составить треугольник.
- При аффинных преобразованиях медиана переходит в медиану.
- Медиана треугольника делит его на две равновеликие части.
Формулы
- Формула медианы через стороны (выводится через теорему Стюарта или достроением до параллелограмма и использованием равенства в параллелограмме суммы квадратов сторон и суммы квадратов диагоналей):
- Формула стороны через медианы:
Если две медианы перпендикулярны, то сумма квадратов сторон, на которые они опущены, в 5 раз больше квадрата третьей стороны.
Мнемоническое правило
Медиана-обезьяна,
у которой зоркий глаз,
прыгнет точно в середину
стороны против вершины,
где находится сейчас.
Примечания
См. также
Ссылки
Wikimedia Foundation . 2010 .
Смотреть что такое "Медиана треугольника" в других словарях:
Медиана: Медиана треугольника в планиметрии, отрезок соединяющий вершину треугольника с серединой противоположной стороны в статистике медианой называется значение совокупности, делящее ранжированный ряд данных пополам Медиана (статистика) … … Википедия
Медиана: Медиана треугольника в планиметрии, отрезок, соединяющий вершину треугольника с серединой противоположной стороны Медиана (статистика) квантиль 0.5 Медиана (трасса) средняя линия трассы, проведённая между правым и левым … Википедия
Треугольник и его медианы. Медиана треугольника ― отрезок внутри треугольника, соединяющий вершину треугольника с серединой противоположной стороны, а также прямая, содержащая этот отрезок. Содержание 1 Свойства 2 Формулы … Википедия
Линия, соединяющая вершину треугольника с серединой его основания. Полный словарь иностранных слов, вошедших в употребление в русском языке. Попов М., 1907. медиана (лат. mediana средняя) 1) геол. отрезок, соединяющий вершину треугольника с… … Словарь иностранных слов русского языка
Медиана (от латинского mediana средняя) в геометрии, отрезок, соединяющий одну из вершин треугольника с серединой противоположной стороны. Три М. треугольника пересекаются в одной точке, которую иногда называют «центром тяжести» треугольника, так … Большая советская энциклопедия
Треугольника прямая (или ее отрезок внутри треугольника), соединяющая вершину треугольника с серединой противоположной стороны. Три М. треугольника пересекаются в одной точке, к рая называется центром тяжести треугольника, центроидом, или… … Математическая энциклопедия
- (от лат. mediana средняя) отрезок, соединяющий вершину треугольника с серединой противоположной стороны … Большой Энциклопедический словарь
МЕДИАНА, медианы, жен. (лат. mediana, букв. средняя). 1. Прямая линия, проведенная от вершины треугольника к середине противолежащей стороны (мат.). 2. В статистике для ряда многих данных величина, обладающая тем свойством, что число данных,… … Толковый словарь Ушакова
МЕДИАНА, ы, жен. В математике: отрезок прямой линии, соединяющий вершину треугольника с серединой противоположной стороны. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
МЕДИАНА (от лат. mediana средняя), отрезок, соединяющий вершину треугольника с серединой противоположной стороны … Энциклопедический словарь
Медиана треугольника - это отрезок, соединяющий верщину треугольника с серединой противолежащей стороны этого треугольника.
Свойства медиан треугольника
1. Медиана разбивает треугольник на два треугольника одинаковой площади.
2. Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины. Эта точка называется центром тяжести треугольника (центроидом).
3. Весь треугольник разделяется своими медианами на шесть равновеликих треугольников.
Длина медианы проведенной к стороне: (док-во достроением до параллелограмма и использованием равенства в параллелограмме удвоенной суммы квадратов сторон и суммы квадратов диагоналей )
Т1.
Три медианы треугольника пересекаются в одной точке М, которая делит каждую из них в отношении 2:1, считая от вершин треугольника. Дано: ∆ABC,
СС 1 , АА 1 , ВВ
1 - медианы
∆ABC
. Доказать: и
Д-во: Пусть М - точка пересечения медиан СС 1 , АА 1 треугольника ABC. Отметим A 2 - середину отрезка AM и С 2 - середину отрезка СМ. Тогда A 2 C 2 - средняя линия треугольника АМС. Значит,А 2 С 2 || АС
и A 2 C 2 = 0,5*АС. С 1 А 1 - средняя линия треугольника ABC. Значит, А 1 С 1 || АС и А 1 С 1 = 0,5*АС.
Четырехугольник А 2 С 1 А 1 С 2 - параллелограмм, так как его противоположные стороны А 1 С 1 и А 2 С 2 равны и параллельны. Следовательно, А 2 М = МА 1 и С 2 М = МC 1 . Это означает, что точки А 2 и M делят медиану АА 2 на три равные части, т. е. AM = 2МА 2 . Аналогично СМ = 2MC 1 . Итак, точка М пересечения двух медиан АА 2 и CC 2 треугольника ABC делит каждую из них в отношении 2:1, считая от вершин треугольника. Совершенно аналогично доказывается, что точка пересечения медиан АА 1 и BB 1 делит каждую из них в отношении 2:1, считая от вершин треугольника.
На медиане АА 1 такой точкой является точка М, следовательно, точка М
и есть точка пересечения медиан АА 1 иBB 1.
Таким образом, n
T2.
Докажите, что отрезки, которые соединяют центроид с вершинами треугольника, делят его на три равновеликие части. Дано: ∆ABC , 
- его медианы.
Доказать:S AMB
=S BMC
=S AMC .
Доказательство.
В,
у них общая. 
т.к. равны их основания 
и высота, проведенная из вершины М,
у них общая. Тогда
Аналогичным образом доказывается, чтоS AMB = S AMC .
Таким образом,S AMB = S AMC = S CMB .
n
Биссектриса треугольника.Теоремы связанные с биссектрисами треугольника. Формулы для нахождения биссектрис
Биссектриса угла - луч с началом в вершине угла, делящий угол на два равных угла.
Биссектриса угла есть геометрическое место точек внутри угла, равноудалённых от сторон угла.
Свойства
1. Теорема о биссектрисе: Биссектриса внутреннего угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон
2. Биссектрисы внутренних углов треугольника пересекаются в одной точке - инцентре - центре вписанной в этот треугольник окружности.
3. Если в треугольнике две биссектрисы равны, то треугольник - равнобедренный (теорема Штейнера - Лемуса).
Вычисление длины биссектрисы
l c - длина биссектрисы, проведённой к стороне c,
a,b,c - стороны треугольника против вершин A,B,C соответственно,
p - полупериметр треугольника,
a l ,b l - длины отрезков, на которые биссектриса l c делит сторону c,
α,β,γ - внутренние углы треугольника при вершинах A,B,C соответственно,
h c - высота треугольника, опущенная на сторону c.
Метод площадей.
Характеристика метода. Из названия следует, что главным объектом данного метода является площадь. Для ряда фигур, например для треугольника, площадь довольно просто выражается через разнообразные комбинации элементов фигуры (треугольника). Поэтому весьма эффективным оказывается прием, когда сравниваются различные выражения для площади данной фигуры. В этом случае возникает уравнение, содержащее известные и искомые элементы фигуры, разрешая которое мы определяем неизвестное. Здесь и проявляется основная особенность метода площадей – из геометрической задачи он «делает» алгебраическую, сводя все к решению уравнения (а иногда системы уравнений).
1) Метод сравнения: связан с большим кол-вом формул S одних и тех же фигур
2) Метод отношения S: основан на след опорных задачах:
Теорема Чевы
Пусть точки A",B",C" лежат на прямых BC,CA,AB треугольника. Прямые AA",BB",CC" пересекаются в одной точке тогда и только тогда, когда 
Доказательство.
Обозначим через точку пересечения отрезков и . Опустим из точек С и А перпендикуляры на прямую ВВ 1 до пересечения с ней в точках Kи L соответственно (см. рисунок).
Поскольку треугольники и имеют общую сторону , то их площади относятся как высоты, проведенные на эту сторону, т.е. AL иCK:
Последнее равенство справедливо, так как прямоугольные треугольники и подобны по острому углу.
Аналогично получаем 
и 
Перемножим эти три равенства:
что и требовалось доказать.
Замечание. Отрезок (или продолжение отрезка), соединяющий вершину треугольника с точкой, лежащей на противоположной стороне или ее продолжении, называется чевианой.
Теорема (обратная теорема Чевы)
. Пусть точки A",B",C" лежат на сторонах BC,CA и AB треугольника ABC соответственно. Пусть выполняется соотношение 
Тогда отрезки AA",BB",CC" и пересекаются в одной точке.
Теорема Менелая
Теорема Менелая. Пусть прямая пересекает треугольник ABC, причем C 1 – точка ее пересечения со стороной AB, A 1 – точка ее пересечения со стороной BC, и B 1 – точка ее пересечения с продолжением стороны AC. Тогда
Доказательство
. Проведем через точку C прямую, параллельную AB. Обозначим через K ее точку пересечения с прямой B 1 C 1 .
ТреугольникиAC 1 B 1 иCKB 1 подобны (∟C 1 AB 1 = ∟KCB 1 , ∟AC 1 B 1 = ∟CKB 1). Следовательно, 
ТреугольникиBC 1 A 1 иCKA 1 такжеподобны (∟BA 1 C 1 =∟KA 1 C, ∟BC 1 A 1 =∟CKA 1). Значит,
Из каждого равенства выразим CK:
Откуда 
что и требовалось доказать.
Теорема (обратная теорема Менелая).
Пусть дан треугольник ABC. Пусть точка C 1 лежит на стороне AB, точка A 1 – на стороне BC, а точка B 1 – на продолжении стороны AC, причем выполняется соотношение
Тогда точки A 1 ,B 1 и C 1 лежат на одной прямой.
