Zvyšovanie a znižovanie intervalov poskytuje veľmi dôležité informácie o správaní funkcie. Ich nájdenie je súčasťou procesu skúmania funkcií a vytvárania grafov. Okrem toho sa pri hľadaní najväčších a najmenších hodnôt funkcie v určitom intervale venuje osobitná pozornosť extrémnym bodom, pri ktorých dochádza k zmene z nárastu na pokles alebo od poklesu k zvýšeniu.
V tomto článku uvedieme potrebné definície, sformulujeme dostatočné kritérium pre nárast a pokles funkcie na intervale a dostatočné podmienky pre existenciu extrému a celú túto teóriu aplikujeme na riešenie príkladov a problémov.
Navigácia na stránke.
Zvyšovanie a znižovanie funkcie na intervale.
Definícia rastúcej funkcie.
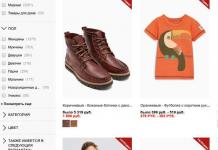
Funkcia y=f(x) narastá na intervale X, ak pre ľubovoľné a ![]() nerovnosť je uspokojená. Inými slovami, väčšia hodnota argumentu zodpovedá väčšej hodnote funkcie.
nerovnosť je uspokojená. Inými slovami, väčšia hodnota argumentu zodpovedá väčšej hodnote funkcie.
Znižujúca sa definícia funkcie.
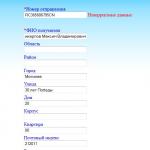
Funkcia y=f(x) klesá na intervale X, ak pre nejaké a ![]() nerovnosť
nerovnosť ![]() . Inými slovami, väčšia hodnota argumentu zodpovedá menšej hodnote funkcie.
. Inými slovami, väčšia hodnota argumentu zodpovedá menšej hodnote funkcie.

POZNÁMKA: ak je funkcia definovaná a spojitá na koncoch intervalu nárastu alebo poklesu (a;b), teda na x=a a x=b , potom sú tieto body zahrnuté do intervalu nárastu alebo poklesu. Toto nie je v rozpore s definíciami rastúcej a klesajúcej funkcie na intervale X .
Napríklad z vlastností základných elementárnych funkcií vieme, že y=sinx je definované a spojité pre všetky reálne hodnoty argumentu. Preto z nárastu funkcie sínus na intervale môžeme uplatniť nárast na intervale .
Extrémne body, funkčné extrémy.
Pointa sa volá maximálny bod funkciu y=f(x), ak nerovnosť platí pre všetky x z jej okolia. Zavolá sa hodnota funkcie v maximálnom bode maximálna funkcia a označujú .
Pointa sa volá minimálny bod funkciu y=f(x), ak nerovnosť platí pre všetky x z jej okolia. Zavolá sa hodnota funkcie v minimálnom bode funkčné minimum a označujú .
Okolie bodu sa chápe ako interval ![]() , kde je dostatočne malé kladné číslo.
, kde je dostatočne malé kladné číslo.
Minimálny a maximálny počet bodov sa nazýva extrémne body a volajú sa hodnoty funkcií zodpovedajúce extrémnym bodom funkčné extrémy.

Nezamieňajte extrémy funkcií s maximálnymi a minimálnymi hodnotami funkcie.

Na prvom obrázku je maximálna hodnota funkcie na segmente dosiahnutá v maximálnom bode a rovná sa maximu funkcie a na druhom obrázku je maximálna hodnota funkcie dosiahnutá v bode x=b , čo nie je maximálny bod.
Dostatočné podmienky pre zvyšovanie a znižovanie funkcií.
Na základe dostatočných podmienok (znakov) pre nárast a pokles funkcie sa zistia intervaly nárastu a poklesu funkcie.
Tu sú formulácie znakov rastúcich a klesajúcich funkcií na intervale:
- ak je derivácia funkcie y=f(x) kladná pre ľubovoľné x z intervalu X , potom sa funkcia zväčší o X ;
- ak je derivácia funkcie y=f(x) záporná pre ľubovoľné x z intervalu X , potom je funkcia na X klesajúca.
Na určenie intervalov nárastu a poklesu funkcie je teda potrebné:
Zvážte príklad nájdenia intervalov rastúcich a klesajúcich funkcií, aby ste objasnili algoritmus.
Príklad.
Nájdite intervaly nárastu a poklesu funkcie.
Riešenie.
Prvým krokom je nájsť rozsah funkcie. V našom príklade by výraz v menovateli nemal zaniknúť, teda .
Prejdime k hľadaniu derivácie funkcie: 
Na určenie intervalov nárastu a poklesu funkcie dostatočným kritériom riešime nerovnice a na definičnom obore. Využime zovšeobecnenie intervalovej metódy. Jediný skutočný koreň čitateľa je x = 2 a menovateľ zaniká pri x = 0 . Tieto body rozdeľujú definičný obor na intervaly, v ktorých si derivácia funkcie zachováva svoje znamienko. Označme tieto body na číselnej osi. Plusmi a mínusmi podmienečne označujeme intervaly, v ktorých je derivácia kladná alebo záporná. Nižšie uvedené šípky schematicky znázorňujú zvýšenie alebo zníženie funkcie na príslušnom intervale. 
Touto cestou,  A
A  .
.
V bode x=2 funkcia je definovaná a spojitá, preto ju treba pridať k vzostupným aj zostupným intervalom. V bode x=0 funkcia nie je definovaná, takže tento bod nie je zahrnutý v požadovaných intervaloch.
Uvádzame graf funkcie na porovnanie získaných výsledkov s ňou.

odpoveď:
Funkcia sa zvyšuje pri ![]() , klesá na intervale (0;2] .
, klesá na intervale (0;2] .
Dostatočné podmienky pre extrém funkcie.
Na nájdenie maxima a minima funkcie môžete použiť ktorýkoľvek z troch extrémnych znamienok, samozrejme, ak funkcia spĺňa ich podmienky. Najbežnejší a najpohodlnejší je prvý z nich.
Prvá postačujúca podmienka pre extrém.
Nech je funkcia y=f(x) diferencovateľná v -okolí bodu a je spojitá v samotnom bode.
Inými slovami:
Algoritmus na nájdenie extrémnych bodov podľa prvého znamienka funkcie extrém.
- Nájdenie rozsahu funkcie.
- Deriváciu funkcie nájdeme na definičnom obore.
- Určíme nuly čitateľa, nuly menovateľa derivácie a body definičného oboru, kde derivácia neexistuje (všetky uvedené body sú tzv. body možného extrému pri prechode cez tieto body môže derivácia len zmeniť svoje znamienko).
- Tieto body rozdeľujú definičný obor funkcie na intervaly, v ktorých si derivácia zachováva svoje znamienko. Znamienka derivácie určíme na každom z intervalov (napríklad výpočtom hodnoty derivácie funkcie v ľubovoľnom bode jedného intervalu).
- Vyberáme body, v ktorých je funkcia spojitá a pri prechode cez ktoré derivácia mení znamienko - sú to krajné body.
Príliš veľa slov, uvažujme o niekoľkých príkladoch hľadania extrémnych bodov a extrémov funkcie pomocou prvej postačujúcej podmienky pre extrém funkcie.
Príklad.
Nájdite extrémy funkcie.
Riešenie.
Rozsah funkcie je celá množina reálnych čísel okrem x=2 .
Nájdeme derivát: 
Nuly v čitateli sú body x=-1 a x=5 , menovateľ ide na nulu pri x=2 . Označte tieto body na číselnej osi 
Určíme znamienka derivácie na každom intervale, preto vypočítame hodnotu derivácie v ktoromkoľvek z bodov každého intervalu, napríklad v bodoch x=-2, x=0, x=3 a x= 6.
Preto je derivácia na intervale kladná (na obrázku nad tento interval vložíme znamienko plus). Podobne 
Preto dávame mínus na druhý interval, mínus na tretí a plus na štvrtý.
Zostáva vybrať body, v ktorých je funkcia spojitá a jej derivácia mení znamienko. Toto sú extrémne body.
V bode x=-1 funkcia je spojitá a derivácia mení znamienko z plus na mínus, preto podľa prvého znamienka extrému je x=-1 maximálny bod, zodpovedá maximu funkcie  .
.
V bode x=5 funkcia je spojitá a derivácia mení znamienko z mínus na plus, preto x=-1 je minimálny bod, zodpovedá minimu funkcie  .
.
Grafické znázornenie.

odpoveď:
UPOZORNENIE: prvý dostatočný znak extrému nevyžaduje, aby bola funkcia diferencovateľná v samotnom bode.
Príklad.
Nájdite extrémne body a extrémy funkcie ![]() .
.
Riešenie.
Oblasťou funkcie je celá množina reálnych čísel. Samotná funkcia môže byť napísaná ako: 
Poďme nájsť deriváciu funkcie: 
V bode x=0 derivát neexistuje, pretože hodnoty jednostranných limitov sa nezhodujú, keď má argument tendenciu k nule: 
Pôvodná funkcia je zároveň spojitá v bode x=0 (pozri časť o skúmaní spojitosti funkcie): 
Nájdite hodnoty argumentu, pri ktorom derivácia zmizne: 
Všetky získané body označíme na reálnej čiare a určíme znamienko derivácie na každom z intervalov. Na tento účel vypočítame hodnoty derivácie v ľubovoľných bodoch každého intervalu, napríklad keď x=-6, x=-4, x=-1, x=1, x=4, x=6.
t.j. 
Teda podľa prvého znaku extrému je minimálny počet bodov ![]() , maximálny počet bodov je
, maximálny počet bodov je ![]() .
.
Vypočítame zodpovedajúce minimá funkcie 
Vypočítame zodpovedajúce maximá funkcie 
Grafické znázornenie.

odpoveď:
 .
.
Druhý znak extrému funkcie.
Ako vidíte, tento znak extrému funkcie vyžaduje existenciu derivácie aspoň do druhého rádu v bode .
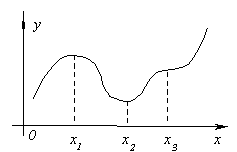
Uvažujme o grafe spojitej funkcie y=f(x) znázornené na obrázku.
Hodnota funkcie v bode X 1 bude väčšia ako hodnoty funkcie vo všetkých susedných bodoch vľavo aj vpravo X jeden . V tomto prípade sa hovorí, že funkcia má v bode X 1 max. V bode X Funkcia 3 má samozrejme aj maximum. Ak vezmeme do úvahy bod X 2, potom je hodnota funkcie v ňom menšia ako všetky susedné hodnoty. V tomto prípade sa hovorí, že funkcia má v bode X 2 minimálne. Podobne k pointe X 4 .
Funkcia y=f(x) v bode X 0 má maximálne, ak je hodnota funkcie v tomto bode väčšia ako jej hodnoty vo všetkých bodoch nejakého intervalu obsahujúceho bod X 0, t.j. ak existuje také okolie bodu X 0, ktorá je pre každého X≠X 0 , patriaci do tejto štvrte, máme nerovnosť f(x)<f(x 0 ) .
Funkcia y=f(x) Má minimálne v bode X 0 , ak existuje také okolie bodu X 0 , čo je pre každého X≠X 0 patriace do tejto štvrte, máme nerovnosť f(x)>f(x0.
Body, v ktorých funkcia dosiahne svoje maximum a minimum, sa nazývajú extrémne body a hodnoty funkcie v týchto bodoch sú extrémy funkcie.
Venujme pozornosť skutočnosti, že funkcia definovaná na segmente môže dosiahnuť svoje maximum a minimum iba v bodoch obsiahnutých v uvažovanom segmente.
Všimnite si, že ak má funkcia v určitom bode maximum, neznamená to, že v tomto bode má funkcia maximálnu hodnotu v celej doméne. Na obrázku diskutovanom vyššie je funkcia v bode X 1 má maximum, aj keď existujú body, v ktorých sú hodnoty funkcie väčšie ako v bode X 1 . najmä f(X 1) < f(X 4) t.j. minimum funkcie je väčšie ako maximum. Z definície maxima len vyplýva, že ide o najväčšiu hodnotu funkcie v bodoch dostatočne blízkych maximálnemu bodu.
Veta 1. (Nevyhnutná podmienka existencie extrému.) Ak je diferencovateľná funkcia y=f(x) má v bode x=x 0 extrém, potom jeho derivácia v tomto bode zmizne.
Dôkaz. Dovoľte, pre istotu, v bode X 0 má funkcia maximum. Potom pre dostatočne malé prírastky Δ X máme f(x 0 + Δ X)
Prechod v týchto nerovnostiach do limitu ako Δ X→ 0 a berúc do úvahy, že derivácia f "(X 0) existuje, a preto limit vľavo nezávisí od toho, ako Δ X→ 0, dostaneme: pre Δ X → 0 – 0 f"(X 0) ≥ 0 a pri A X → 0 + 0 f"(X 0) ≤ 0. Keďže f"(X 0) definuje číslo, potom sú tieto dve nerovnosti kompatibilné iba vtedy, ak f"(X 0) = 0.
Dokázaná veta hovorí, že maximálne a minimálne body môžu byť iba medzi tými hodnotami argumentu, pre ktoré derivácia zmizne.
Uvažovali sme o prípade, keď funkcia má deriváciu vo všetkých bodoch určitého segmentu. Čo sa stane, keď derivát neexistuje? Zvážte príklady.
Príklady.
- r=|X|.
Funkcia nemá deriváciu v bode X=0 (v tomto bode graf funkcie nemá určitú dotyčnicu), ale v tomto bode má funkcia minimum, keďže r(0)=0 a pre všetkých X≠ 0r > 0.
- Nechať byť X< x
0 Potom c< x
0 a f "(c)> 0.
Preto f "(c)(x-x 0)<
0 a teda
f(x) - f(x 0 )< 0, t.j. f(x)< f(x 0 ).
- Nechať byť x > x 0 Potom c> x 0 a f" (c)< 0. Prostriedky f "(c)(x-x 0)< 0. Preto f(x) - f(x 0 ) <0,т.е.f(x)< f(x 0 ) .
- Nájdite rozsah funkcie f(x).
- Nájdite prvú deriváciu funkcie f"(x).
- Na tento účel určite kritické body:
- nájsť skutočné korene rovnice f"(x)=0;
- nájsť všetky hodnoty X pod ktorým derivát f"(x) neexistuje.
- Určite znamienko derivácie vľavo a vpravo od kritického bodu. Keďže znamienko derivácie zostáva konštantné medzi dvoma kritickými bodmi, stačí určiť znamienko derivácie v ktoromkoľvek bode vľavo a v jednom bode vpravo od kritického bodu.
- Vypočítajte hodnotu funkcie v extrémnych bodoch.
- Nájdite všetky kritické body funkcie v intervale ( a, b) a vypočítajte funkčné hodnoty v týchto bodoch.
- Vypočítajte hodnoty funkcie na koncoch segmentu pre x=a, x=b.
- Zo všetkých získaných hodnôt vyberte najväčšiu a najmenšiu.
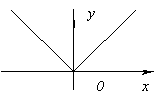
Funkcia nemá deriváciu at X=0, pretože to ide do nekonečna, keď X=0. Ale v tomto bode má funkcia maximum.
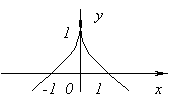
Funkcia nemá deriváciu at X=0 pretože ![]() pri X→0. V tomto bode funkcia nemá ani maximum, ani minimum. naozaj, f(x)=0 a pri X<0f(x)<0, а при X>0f(x)>0.
pri X→0. V tomto bode funkcia nemá ani maximum, ani minimum. naozaj, f(x)=0 a pri X<0f(x)<0, а при X>0f(x)>0.

Z uvedených príkladov a formulovanej vety je teda zrejmé, že funkcia môže mať extrém iba v dvoch prípadoch: 1) v bodoch, kde derivácia existuje a je rovná nule; 2) v bode, kde derivát neexistuje.
Ak však v určitom okamihu X 0 to vieme f"(x 0 ) =0, potom z toho nemožno usudzovať, že v bode X 0 funkcia má extrém.
Napríklad. ![]() .
.

Ale bod X=0 nie je extrémny bod, pretože naľavo od tohto bodu sú funkčné hodnoty umiestnené pod osou Vôl a vyššie vpravo.
Hodnoty argumentu z oblasti funkcie, pre ktoré derivácia funkcie zaniká alebo neexistuje, sa nazývajú kritických bodov.
Z uvedeného vyplýva, že extrémy funkcie patria medzi kritické body a nie každý kritický bod je však extrémnym bodom. Preto, aby ste našli extrém funkcie, musíte nájsť všetky kritické body funkcie a potom v každom z týchto bodov samostatne preskúmať maximum a minimum. Na to slúži nasledujúca veta.
Veta 2. (Postačujúca podmienka pre existenciu extrému.) Nech je funkcia spojitá na nejakom intervale obsahujúcom kritický bod X 0 a je diferencovateľná vo všetkých bodoch tohto intervalu (možno okrem samotného bodu X 0). Ak pri prechode zľava doprava cez tento bod derivácia zmení znamienko z plus na mínus, potom v bode X = X 0 má funkcia maximum. Ak pri prechode cez X 0 zľava doprava, derivácia zmení znamienko z mínus na plus, potom má funkcia v tomto bode minimum.
Teda ak
Dôkaz. Najprv predpokladajme, že pri prechode X 0, derivácia mení znamienko z plus na mínus, t.j. pre všetkých X blízko k veci X 0 f "(x)> 0 pre X< x 0 , f"(x)< 0 pre x > x 0 Aplikujme na rozdiel Lagrangeovu vetu f(x) - f(x 0 ) = f "(c)(x-x 0), kde c leží medzi X A X 0 .
Teda pre všetky hodnoty X dostatočne blízko X 0 f(x)< f(x 0 ) . A to znamená, že v bode X 0 má funkcia maximum.
Druhá časť vety o minime je dokázaná podobne.
Znázornime význam tejto vety na obrázku. Nechať byť f"(x 1 ) =0 a pre ľubovoľné X, dostatočne blízko X 1, nerovnosti
f"(x)< 0 pri X< x 1 , f "(x)> 0 pri x > x 1 .
Potom vľavo od bodu X 1 funkcia je rastúca a klesajúca vpravo, teda keď X = X 1 funkcia prechádza od rastúcej k klesajúcej, to znamená, že má maximum.
Podobne možno zvážiť body X 2 a X 3 .

Schematicky možno všetko vyššie znázorniť na obrázku:
Pravidlo pre štúdium funkcie y=f(x) pre extrém
Príklady. Preskúmajte funkcie pre minimum a maximum.
NAJVÄČŠIE A MINIMÁLNE FUNKČNÉ HODNOTY NA ODpočúvaní
najväčší hodnota funkcie v segmente je najväčšia zo všetkých jej hodnôt v tomto segmente a najmenej je najmenšia zo všetkých jej hodnôt.
Zvážte funkciu y=f(x) súvislé na intervale [ a, b]. Ako je známe, takáto funkcia dosahuje svoje maximálne a minimálne hodnoty buď na hranici segmentu, alebo v ňom. Ak sa maximálna alebo minimálna hodnota funkcie dosiahne vo vnútornom bode segmentu, potom je táto hodnota maximom alebo minimom funkcie, to znamená, že sa dosiahne v kritických bodoch.
Dostávame teda nasledovné pravidlo na nájdenie najväčších a najmenších hodnôt funkcie na segmente [ a, b] :
Predtým, ako sa naučíme, ako nájsť extrém funkcie, je potrebné pochopiť, čo je extrém. Najvšeobecnejšia definícia extrému hovorí, že ide o najmenšiu alebo najväčšiu hodnotu funkcie používanej v matematike na určitej množine číselnej osi alebo grafu. V mieste, kde je minimum, sa objaví extrém minima a kde je maximum, objaví sa extrém maxima. Aj v takej disciplíne, akou je matematická analýza, sa rozlišujú lokálne extrémy funkcie. Teraz sa pozrime na to, ako nájsť extrémy.
Extrémy v matematike patria medzi najdôležitejšie charakteristiky funkcie, vykazujú jej najväčšiu a najmenšiu hodnotu. Extrémy sa nachádzajú najmä v kritických bodoch nájdených funkcií. Stojí za zmienku, že práve v extrémnom bode funkcia radikálne mení svoj smer. Ak vypočítame deriváciu extrémneho bodu, potom sa podľa definície musí rovnať nule, inak bude úplne chýbať. Ak sa chcete naučiť, ako nájsť extrém funkcie, musíte vykonať dve po sebe nasledujúce úlohy:
- nájsť deriváciu funkcie, ktorá musí byť určená úlohou;
- nájsť korene rovnice.
Postupnosť hľadania extrému
- Napíšte funkciu f(x), ktorá je daná. Nájdite jeho deriváciu prvého rádu f "(x). Výsledný výraz prirovnajte k nule.
- Teraz musíte vyriešiť rovnicu, ktorá sa ukázala. Výsledné riešenia budú koreňmi rovnice, ako aj kritickými bodmi definovanej funkcie.
- Teraz určíme, ktoré kritické body (maximum alebo minimum) sú nájdené korene. Ďalším krokom, keď sme sa naučili nájsť extrémne body funkcie, je nájsť druhú deriváciu požadovanej funkcie f "(x). Bude potrebné dosadiť hodnoty nájdených kritických bodov do konkrétnej nerovnosti a potom vypočítajte, čo sa stane. Ak sa to stane, že druhá derivácia sa ukáže byť väčšia ako nula v kritickom bode, potom to bude minimálny bod a inak maximálny bod.
- Zostáva vypočítať hodnotu počiatočnej funkcie v požadovaných maximálnych a minimálnych bodoch funkcie. Za týmto účelom nahradíme získané hodnoty do funkcie a vypočítame. Treba však poznamenať, že ak sa kritický bod ukáže ako maximum, potom extrém bude maximálny, a ak je to minimum, potom bude analogicky minimum.
Algoritmus na nájdenie extrému
Aby sme zhrnuli získané poznatky, urobme krátky algoritmus, ako nájsť extrémne body.
- Nájdeme definičný obor danej funkcie a jej intervaly, ktoré presne určujú, na akých intervaloch je funkcia spojitá.
- Nájdeme deriváciu funkcie f "(x).
- Vypočítame kritické body rovnice y = f (x).
- Analyzujeme zmeny v smere funkcie f(x), ako aj znamienko derivácie f"(x), kde kritické body oddeľujú definičný obor tejto funkcie.
- Teraz určíme, či je každý bod na grafe maximum alebo minimum.
- Hodnoty funkcie nájdeme v tých bodoch, ktoré sú extrémy.
- Opravujeme výsledok tejto štúdie - extrémy a intervaly monotónnosti. To je všetko. Teraz sme zvážili, ako nájsť extrém na akomkoľvek intervale. Ak potrebujete nájsť extrém na určitom intervale funkcie, potom sa to robí podobným spôsobom, nevyhnutne sa berú do úvahy iba hranice vykonávaného výskumu.
Takže sme zvážili, ako nájsť extrémne body funkcie. Pomocou jednoduchých výpočtov, ako aj vedomostí o hľadaní derivátov môžete nájsť akýkoľvek extrém a vypočítať ho, ako aj graficky označiť. Hľadanie extrémov je jednou z najdôležitejších častí matematiky v škole aj na vysokej škole, takže ak sa naučíte, ako ich správne určiť, učenie bude oveľa jednoduchšie a zaujímavejšie.
Jednoduchý algoritmus na hľadanie extrémov..
- Hľadanie derivácie funkcie
- Prirovnajte túto deriváciu k nule
- Nájdeme hodnoty premennej výsledného výrazu (hodnoty premennej, pri ktorej sa derivácia prevedie na nulu)
- Súradnicovú čiaru rozdeľujeme na intervaly s týmito hodnotami (zároveň by sme nemali zabúdať na body zlomu, ktoré je tiež potrebné vykresliť na čiaru), všetky tieto body sa nazývajú „podozrivé“ body pre extrém
- Vypočítame, na ktorom z týchto intervalov bude derivácia kladná a na ktorom záporná. Aby ste to dosiahli, musíte nahradiť hodnotu z intervalu do derivácie.
Z bodov podozrivých z extrému je potrebné nájsť presne . Aby sme to dosiahli, pozrieme sa na naše medzery na súradnicovej čiare. Ak sa pri prechode cez nejaký bod zmení znamienko derivácie z plus na mínus, potom bude tento bod maximálne, a ak z mínusu do plusu, tak minimálne.
Ak chcete nájsť najväčšiu a najmenšiu hodnotu funkcie, musíte vypočítať hodnotu funkcie na koncoch segmentu a v extrémnych bodoch. Potom vyberte najväčšiu a najmenšiu hodnotu.
Zvážte príklad
Nájdeme deriváciu a prirovnáme ju k nule:
Získané hodnoty premenných aplikujeme na súradnicovú čiaru a vypočítame znamienko derivácie na každom z intervalov. No napríklad na prvý záber-2
, potom bude derivát-0,24
, na druhý odber0
, potom bude derivát2
, a do tretice berieme2
, potom bude derivát-0,24. Položili sme príslušné značky.
Vidíme, že pri prechode bodom -1 derivácia zmení znamienko z mínus na plus, to znamená, že to bude minimálny bod a pri prechode cez 1 z plusu do mínusu je to maximálny bod.
Prejdime na graf funkcie y \u003d x 3 - 3x 2. Uvažujme okolie bodu x = 0, t.j. nejaký interval obsahujúci tento bod. Je logické, že existuje také okolie bodu x \u003d 0, že funkcia y \u003d x 3 - 3x 2 v tomto susedstve nadobúda najväčšiu hodnotu v bode x \u003d 0. Napríklad na intervale (- 1; 1) najväčšiu hodnotu rovnajúcu sa 0, funkcia nadobúda v bode x = 0. Bod x = 0 sa nazýva maximálny bod tejto funkcie.
Podobne sa bod x \u003d 2 nazýva minimálny bod funkcie x 3 - 3x 2, pretože v tomto bode hodnota funkcie nie je väčšia ako jej hodnota v inom bode v blízkosti bodu x \u003d 2 , napríklad okolie (1,5; 2,5).
Maximálny bod funkcie f (x) je teda bod x 0, ak existuje okolie bodu x 0 - také, že nerovnosť f (x) ≤ f (x 0) je splnená pre všetky x z tohto okolia. .
Napríklad bod x 0 \u003d 0 je maximálny bod funkcie f (x) \u003d 1 - x 2, pretože f (0) \u003d 1 a nerovnosť f (x) ≤ 1 platí pre všetky hodnoty z x.
Minimálny bod funkcie f (x) sa nazýva bod x 0, ak existuje také okolie bodu x 0, že nerovnosť f (x) ≥ f (x 0) je splnená pre všetky x z tohto okolia.
Napríklad bod x 0 \u003d 2 je minimálny bod funkcie f (x) \u003d 3 + (x - 2) 2, pretože f (2) \u003d 3 a f (x) ≥ 3 pre všetky x .
Extrémne body sa nazývajú minimálne body a maximálne body.
Vráťme sa k funkcii f(x), ktorá je definovaná v niektorom okolí bodu x 0 av tomto bode má deriváciu.
Ak x 0 je extrémny bod diferencovateľnej funkcie f (x), potom f "(x 0) \u003d 0. Toto tvrdenie sa nazýva Fermatova veta.
Fermatova veta má jasný geometrický význam: v extrémnom bode je dotyčnica rovnobežná s osou x, a preto je jej sklon
f "(x 0) je nula.
Napríklad funkcia f (x) \u003d 1 - 3x 2 má maximum v bode x 0 \u003d 0, jej derivácia f "(x) \u003d -2x, f "(0) \u003d 0.
Funkcia f (x) \u003d (x - 2) 2 + 3 má minimum v bode x 0 \u003d 2, f "(x) \u003d 2 (x - 2), f "(2) \u003d 0 .
Všimnite si, že ak f "(x 0) \u003d 0, potom to nestačí na tvrdenie, že x 0 je nevyhnutne extrémny bod funkcie f (x).
Napríklad, ak f (x) \u003d x 3, potom f "(0) \u003d 0. Bod x \u003d 0 však nie je extrémnym bodom, pretože funkcia x 3 sa zvyšuje na celej reálnej osi.
Extrémne body diferencovateľnej funkcie teda treba hľadať iba medzi koreňmi rovnice
f "(x) \u003d 0, ale koreň tejto rovnice nie je vždy extrémnym bodom.
Stacionárne body sú body, v ktorých sa derivácia funkcie rovná nule.
Aby bol teda bod x 0 extrémnym bodom, je potrebné, aby bol stacionárnym bodom.
Zvážte dostatočné podmienky na to, aby stacionárny bod bol extrémnym bodom, t.j. podmienky, za ktorých je stacionárny bod minimálnym alebo maximálnym bodom funkcie.
Ak je derivácia naľavo od stacionárneho bodu kladná a napravo záporná, t.j. derivácia zmení znamienko "+" na znamienko "-" pri prechode týmto bodom, potom je tento stacionárny bod maximálnym bodom.
V tomto prípade sa totiž vľavo od stacionárneho bodu funkcia zvyšuje a vpravo klesá, t.j. tento bod je maximálny bod.
Ak derivácia zmení znamienko "-" na znamienko "+" pri prechode cez stacionárny bod, potom tento stacionárny bod je minimálny bod.
Ak derivácia pri prechode stacionárnym bodom nemení znamienko, t.j. derivácia je kladná alebo záporná vľavo a vpravo od stacionárneho bodu, potom tento bod nie je extrémnym bodom.
Pozrime sa na jednu z úloh. Nájdite extrémne body funkcie f (x) \u003d x 4 - 4x 3.
Riešenie.
1) Nájdite deriváciu: f "(x) \u003d 4x 3 - 12x 2 \u003d 4x 2 (x - 3).
2) Nájdite stacionárne body: 4x 2 (x - 3) \u003d 0, x 1 \u003d 0, x 2 \u003d 3.
3) Pomocou intervalovej metódy zistíme, že derivácia f "(x) \u003d 4x 2 (x - 3) je kladná pre x\u003e 3, záporná pre x< 0 и при 0 < х < 3.
4) Keďže pri prechode bodom x 1 \u003d 0 sa znamienko derivácie nemení, tento bod nie je extrémnym bodom.
5) Pri prechode bodom x 2 \u003d 3 derivácia zmení znamienko "-" na znamienko "+". Preto je x 2 \u003d 3 minimálny bod.
stránky, s úplným alebo čiastočným kopírovaním materiálu, je potrebný odkaz na zdroj.