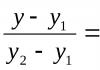План на урока.

1. Организационен момент.

2. Представяне на материала.

3. Домашна работа.

4. Обобщаване на урока.

По време на часовете

I. Организационен момент.

II. Представяне на материала.

Мотивация.

Разширяването на набора от реални числа е, че към реалните числа се добавят нови числа (въображаеми). Въвеждането на тези числа е свързано с невъзможността да се извлече корен от отрицателно число в набора от реални числа.

Въвеждане на понятието комплексно число.

Въображаемите числа, с които допълваме реалните числа, се записват като би, където iЕ въображаема единица и i 2 = - 1.

Въз основа на това получаваме следното определение на комплексно число.

Определение... Комплексното число е израз на формата a + bi, където аи б- реални числа. В този случай са изпълнени следните условия:

а) Две комплексни числа a 1 + b 1 iи a 2 + b 2 iса равни тогава и само тогава a 1 = a 2, b 1 = b 2.

б) Добавянето на комплексни числа се определя от правилото:

(a 1 + b 1 i) + (a 2 + b 2 i) = (a 1 + a 2) + (b 1 + b 2) i.

в) Умножаването на комплексни числа се определя от правилото:

(a 1 + b 1 i) (a 2 + b 2 i) = (a 1 a 2 - b 1 b 2) + (a 1 b 2 - a 2 b 1) i.

Алгебрична форма на комплексно число.

Записване на комплексно число във формата a + biсе нарича алгебрична форма на комплексно число, където но- реална част, биЕ въображаемата част и бРеално число е.

Комплексен номер a + biсе счита за равна на нула, ако реалната и въображаемата й част са равни на нула: a = b = 0

Комплексен номер a + biпри b = 0се счита за същото като реално число а: a + 0i = a.

Комплексен номер a + biпри а = 0се нарича чисто въображаем и се обозначава би: 0 + bi = bi.

Две комплексни числа z = a + biи = а - бикоито се различават само по знака на въображаемата част, се наричат ​​спрегнати.

Действия върху комплексни числа в алгебрична форма.

Можете да направите следното за комплексните числа в алгебрична форма.

1) Добавяне.

Определение... Сумата от комплексни числа z 1 = a 1 + b 1 iи z 2 = a 2 + b 2 iсе нарича комплексно число z, реалната част на която е равна на сумата от реалните части z 1и z 2, а въображаемата част е сумата от въображаемите части на числата z 1и z 2, т.е. z = (a 1 + a 2) + (b 1 + b 2) i.

Числата z 1и z 2се наричат ​​термини.

Добавянето на комплексни числа има следните свойства:

1º. Коммутабилност: z 1 + z 2 = z 2 + z 1.

2º. Асоциативност: (z 1 + z 2) + z 3 = z 1 + (z 2 + z 3).

3º. Комплексен номер –A –biсе нарича противоположност на комплексно число z = a + bi... Комплексно число, противоположно на комплексно число z, означени -z... Сума от комплексни числа zи -zе нула: z + (-z) = 0

Пример 1. Извършете добавяне (3 - i) + (-1 + 2i).

(3-i) + (-1 + 2i) = (3 + (-1)) + (-1 + 2) i = 2 + 1i.

2) Изваждане.

Определение.Извадете от комплексно число z 1комплексно число z 2 z,Какво z + z 2 = z 1.

Теорема... Разликата в комплексните числа съществува и освен това е уникална.

Пример 2. Извършете изваждане (4 - 2i) - (-3 + 2i).

(4 - 2i) - (-3 + 2i) = (4 - (-3)) + (-2 - 2) i = 7 - 4i.

3) Умножение.

Определение... Произведението на комплексни числа z 1 = a 1 + b 1 iи z 2 = a 2 + b 2 iсе нарича комплексно число zопределено от равенството: z = (a 1 a 2 - b 1 b 2) + (a 1 b 2 + a 2 b 1) i.

Числата z 1и z 2се наричат ​​фактори.

Умножаването на комплексни числа има следните свойства:

1º. Коммутабилност: z 1 z 2 = z 2 z 1.

2º. Асоциативност: (z 1 z 2) z 3 = z 1 (z 2 z 3)

3º. Разпределение на умножението спрямо събирането:

(z 1 + z 2) z 3 = z 1 z 3 + z 2 z 3.

4º. z = (a + bi) (a - bi) = a 2 + b 2е реално число.

На практика умножението на комплексни числа се извършва съгласно правилото за умножаване на сумата по сумата и разделяне на реалната и въображаемата части.

В следващия пример ще разгледаме умножаването на комплексни числа по два начина: по правило и умножение на сумата по сумата.

Пример 3. Извършете умножение (2 + 3i) (5 - 7i).

1 начин. (2 + 3i) (5- 7i) = (2 × 5- 3 × (- 7)) + (2 × (- 7) + 3 × 5) i = = (10 + 21) + (- 14 + 15 ) i = 31 + i.

Метод 2. (2 + 3i) (5 - 7i) = 2 × 5 + 2 × ( - 7i) + 3i × 5 + 3i × ( - 7i) = = 10 - 14i + 15i + 21 = 31 + i.

4) Разделение.

Определение... Разделете комплексно число z 1върху комплексно число z 2, след това намерете такова комплексно число z, Какво z z 2 = z 1.

Теорема.Коефициентът на комплексните числа съществува и е уникален, ако z 2 ≠ 0 + 0i.

На практика коефициентът на комплексните числа се намира чрез умножаване на числителя и знаменателя по конюгата на знаменателя.

Нека бъде z 1 = a 1 + b 1 i, z 2 = a 2 + b 2 i, тогава

.

В следващия пример ще разделим по формулата и правилото за умножение по конюгата на знаменателя.

Пример 4. Намерете коефициента .

5) Повишаване до положително цяло число.

а) Силите на въображаемата единица.

Използване на равенството i 2 = -1, лесно е да се определи всяка положителна цяло число на въображаемата единица. Ние имаме:

i 3 = i 2 i = -i,

i 4 = i 2 i 2 = 1,

i 5 = i 4 i = i,

i 6 = i 4 i 2 = -1,

i 7 = i 5 i 2 = -i,

i 8 = i 6 i 2 = 1и т.н.

Това показва, че стойностите на степента i n, където н- положително цяло число, периодично повтаряно, когато индикаторът се увеличи с 4 .

Следователно, за да се увеличи броят iдо положителна степен степента трябва да бъде разделена на 4 и изправен iна степента, показателят на която е равен на остатъка от делението.

Пример 5. Изчислете: (i 36 + i 17) i 23.

i 36 = (i 4) 9 = 1 9 = 1,

i 17 = i 4 × 4 + 1 = (i 4) 4 × i = 1 i = i.

i 23 = i 4 × 5 + 3 = (i 4) 5 × i 3 = 1 · i 3 = - i.

(i 36 + i 17) i 23 = (1 + i) ( - i) = - i + 1 = 1 - i.

б) Повишаването на комплексно число до положително цяло число се извършва съгласно правилото за повдигане на бином до съответната степен, тъй като това е частен случай на умножаване на същите комплексни фактори.

Пример 6. Изчислете: (4 + 2i) 3

(4 + 2i) 3 = 4 3 + 3 × 4 2 × 2i + 3 × 4 × (2i) 2 + (2i) 3 = 64 + 96i - 48 - 8i = 16 + 88i.

ОПРЕДЕЛЕНИЕ

Алгебричната форма на комплексно число е да се запише комплексното число \ (\ z \) под формата \ (\ z = x + iy \), където \ (\ x \) и \ (\ y \) са реални числа , \ (\ i \) е въображаема единица, отговаряща на съотношението \ (\ i ^ (2) = - 1 \)

Числото \ (\ x \) се нарича реална част от комплексното число \ (\ z \) и се обозначава \ (\ x = \ име на оператор (Re) z \)

Числото \ (\ y \) се нарича въображаема част от комплексното число \ (\ z \) и се обозначава \ (\ y = \ име на оператор (Im) z \)

Например:

Комплексният номер \ (\ z = 3-2 i \) и свързаният с него номер \ (\ \ overline (z) = 3 + 2 i \) са написани в алгебрична форма.

Въображаемата стойност \ (\ z = 5 i \) се записва в алгебрична форма.

Освен това, в зависимост от решаващия се проблем, можете да преобразувате комплексно число в тригонометрично или експоненциално.

Нека си припомним необходимата информация за комплексните числа.

Комплексен номере израз на формата а + би, където а, бса реални числа и i- т.нар въображаема единица, символ, чийто квадрат е -1, т.е. i 2 = -1. Номер аНаречен реална части номера б - въображаема часткомплексно число z = а + би... Ако б= 0, тогава вместо а + 0iпишете просто а... Вижда се, че реалните числа са частен случай на комплексни числа.

Аритметичните операции върху комплексни числа са същите като при реални: те могат да се събират, изваждат, умножават и разделят помежду си. Събирането и изваждането се извършва съгласно правилото ( а + би) ± ( ° С + ди) = (а ± ° С) + (б ± д)iи умножение - според правилото ( а + би) · ( ° С + ди) = (ак – бд) + (реклама + пр.н.е.)i(тук се използва само това i 2 = –1). Брой = а – биНаречен сложен конюгатДа се z = а + би... Равенство z · = а 2 + б 2 ви позволява да разберете как да разделите едно комплексно число на друго (ненулево) комплексно число:

(Например, .)

Комплексните числа имат удобно и интуитивно геометрично представяне: числото z = а + биможе да се представи с вектор с координати ( а; б) на декартовата равнина (или, което е почти същото, точка - краят на вектора с тези координати). В този случай сумата от две комплексни числа се изобразява като сума от съответните вектори (които могат да бъдат намерени чрез правилото за паралелограма). Според питагорейската теорема дължината на вектора с координати ( а; б) е равно на. Това количество се нарича модулкомплексно число z = а + бии се обозначава с | z|. Ъгълът, който този вектор прави с положителната посока на оста на абсцисата (отброен обратно на часовниковата стрелка), се нарича аргументкомплексно число zи се обозначава с Arg z... Аргументът не е еднозначно дефиниран, а само до добавяне на кратно на 2 π радиани (или 360 °, ако броите в градуси) - в края на краищата е ясно, че въртенето под такъв ъгъл около началото няма да промени вектора. Но ако векторът на дължината rобразува ъгъл φ с положителна посока на оста на абсцисата, тогава нейните координати са ( r Cos φ ; rГрех φ ). Оттам се оказва тригонометрична нотациякомплексен номер: z = |z| (Cos (Arg z) + iгрях (Арг z)). Често е удобно да се пишат сложни числа в тази форма, защото това значително опростява изчисленията. Умножаването на комплексни числа в тригонометрична форма изглежда много просто: zедин · z 2 = |z 1 | · | z 2 | (Cos (Arg z 1 + Arg z 2) + iгрях (Арг z 1 + Arg z 2)) (при умножаване на две комплексни числа модулите им се умножават и се добавят аргументите). Оттук следвайте Формули на Moivre: z n = |z|н(Cos ( н(Арг z)) + iгрех ( н(Арг z))). С помощта на тези формули е лесно да се научите как да извличате корени от всякаква степен от комплексни числа. N -ти корен от zе толкова комплексно число w, Какво w n = z... Ясно е, че , И къде кможе да вземе всяка стойност от множеството (0, 1, ..., н- един). Това означава, че винаги има точно нкорени н-та степен на комплексно число (в равнината те са разположени във върховете на правилното н-гон).

Комплексните числа са продължение на множеството реални числа, обикновено обозначавани с. Всяко комплексно число може да бъде представено като формална сума, където и са реални числа, е въображаема единица.

Записването на комплексно число под формата ,, се нарича алгебрична форма на комплексно число.

Свойства на комплексни числа. Геометрична интерпретация на комплексно число.

Действия върху комплексни числа, дадени в алгебрична форма:

Помислете за правилата, по които се извършват аритметични операции върху комплексни числа.

Като се имат предвид две комплексни числа α = a + bi и β = c + di, тогава

α + β = (a + bi) + (c + di) = (a + c) + (b + d) i,

α - β = (a + bi) - (c + di) = (a - c) + (b - d) i. (единадесет)

Това следва от дефиницията на операциите за събиране и изваждане на две подредени двойки реални числа (вижте формулите (1) и (3)). Получихме правилата за събиране и изваждане на комплексни числа: за да добавите две комплексни числа, трябва отделно да добавите техните реални части и съответно въображаемите им части; за да се извади друго от едно комплексно число, е необходимо да се извадят съответно техните реални и въображаеми части.

Числото - α = - a - bi се нарича обратното на числото α = a + bi. Сумата от тези две числа е нула:- α + α = (- a- bi) + (a + bi) = (-a + a) + (-b + b) i = 0.

За да получим правилото за умножение на комплексни числа, използваме формула (6), тоест факта, че i2 = -1. Като вземем предвид това отношение, намираме (a + bi) (c + di) = ac + adi + bci + bdi2 = ac + (ad + bc) i - bd, т.е.

(a + bi) (c + di) = (ac - bd) + (ad + bc) i. (12)

Тази формула съответства на формула (2), която дефинира умножението на подредени двойки реални числа.

Обърнете внимание, че сумата и произведението на две сложни спрегнати числа са реални числа. Всъщност, ако α = a + bi, = a - bi, тогава α = (a + bi) (a - bi) = a2 - i2b2 = a2 + b2, α + = (a + bi) + (a - bi ) = (a + a) + (b - b) i = 2a, т.е.

α + = 2a, α = a2 + b2. (13)

Когато разделяме две комплексни числа в алгебрична форма, трябва да очакваме, че частното се изразява и с число от същата форма, тоест α / β = u + vi, където u, v R. Нека изведем правилото за разделяне комплексни числа. Нека са дадени числа α = a + bi, β = c + di и β ≠ 0, тоест c2 + d2 ≠ 0. Последното неравенство означава, че c и d не изчезват едновременно (с изключение на случая, когато c = 0 , d = 0). Прилагайки формула (12) и втората на равенства (13), намираме:

Следователно коефициентът на две комплексни числа се определя по формулата:

съответстващ на формула (4).

Използвайки получената формула за числото β = c + di, можете да намерите неговото обратно число β-1 = 1 / β. Поставяйки a = 1 и b = 0 във формула (14), получаваме

Тази формула определя обратната стойност на дадено ненулево комплексно число; това число също е сложно.

Например: (3 + 7i) + (4 + 2i) = 7 + 9i;

(6 + 5i) - (3 + 8i) = 3 - 3i;

(5 - 4i) (8 - 9i) = 4 - 77i;

Действия върху комплексни числа в алгебрична форма.

55. Аргумент на комплексно число. Тригонометрична нотация на комплексно число (изход).

Arg.com.number. - между положителната посока на реалната ос X по вектора, представляващ даденото число.

Формула тригон. Числа :,