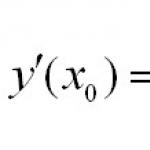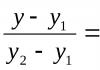ПЪРВИ ДЕРИВАТИВ
ПЪРВИ ДЕРИВАТИВ
(първо производно)Скоростта на нарастване на стойността на функция с увеличаване на нейния аргумент във всяка точка, ако самата функция е дефинирана в тази точка. На графиката първата производна на функция показва ъгъла на нейния наклон. Ако y = f (x),първата му производна в точката x0е границата, към която се стреми f (x0 + a) –f (x0) / aкато ноклони към безкрайно малка стойност. Първата производна може да се обозначи dy / dxили y´ (x).Функция y (x)има постоянна стойност в точката x0,ако dy / dxв точката x0е равна на нула. Първата производна, равна на нула, е необходимо, но недостатъчно условие функцията да достигне своя максимум или минимум в дадена точка.
Икономика. Речник. - М.: „ИНФРА-М“, Издателство „Вес Мир“. Дж. Блек. Общо издание: Доктор по икономика Осадчая И.М.. 2000 .
Икономически речник. 2000 .
Вижте какво е „ПЪРВИ ДЕРИВАТИВ“ в други речници:
- (производно) Степента на нарастване на стойността на функция с увеличение на нейния аргумент във всяка точка, ако самата функция е дефинирана в тази точка. На графиката първата производна на функция показва ъгъла на нейния наклон. Ако y = f (x), първата му производна в точката ... ... Икономически речник
Този термин има други значения, вижте Производен. Илюстрация на концепцията за производна производна ... Уикипедия
Производната е основната концепция за диференциалното смятане, която характеризира скоростта на промяна на функция. Определя се като границата на съотношението на приращението на функция към нарастването на нейния аргумент, когато нарастването на аргумента се стреми към нула, ако има такова ограничение ... ... Уикипедия
Проблем с гранична стойност от специален тип; се състои в намирането на променливите x = (x1, ..., xn) в областта D. Решенията на диференциалното уравнение (1) от четен ред 2m от дадените стойности на всички производни от порядък не по -високи от m на граница S на домейн D (или част от него) ... Енциклопедия по математика
- (втора производна) Първата производна на първата производна на функцията. Първата производна измерва наклона на функцията; втората производна измерва как наклонът се променя с увеличаване на аргумента. Втора производна на y = f (x) ... ... Икономически речник
Тази статия или раздел се нуждае от преработка. Моля, подобрете статията в съответствие с правилата за писане на статии. Дробни професионални ... Уикипедия
- (кръстосана частична производна) Ефектът от промяната на един аргумент на функция от две или повече променливи върху производната на дадена функция, взета от друг аргумент. Ако y = f (x, z), тогава нейната производна или първата производна на функцията y по отношение на аргумента x е равна на ... ... Икономически речник
точкова скорост аналог- Първата производна на изместването на точката по обобщената координата на механизма ...
ъглова скорост на аналог- Първата производна на ъгъла на въртене на връзката по отношение на обобщената координата на механизма ... Политехнически терминологичен обяснителен речник
обобщена скорост на механизма- Първата производна на обобщената координата на механизма във времето ... Политехнически терминологичен обяснителен речник
Книги
- Сборник задачи в диференциалната геометрия и топология, Мищенко А.С.
- Моите научни статии. Книга 3. Метод на матрицата на плътността в квантовите теории на лазер, произволен атом, Борис Владимирович Бондарев. Тази книга преглежда публикувани научни статии, в които нови квантови теории за лазер, произволен атом и амортизиран квантов осцилатор са представени чрез метода на матрицата на плътността. ...
Абсолютно невъзможно е да се решават физически задачи или примери в математиката без познаване на производната и методите за нейното изчисляване. Производната е една от най -важните концепции на математическия анализ. Решихме да посветим днешната статия на тази фундаментална тема. Какво е производна, какъв е нейният физически и геометричен смисъл, как да се изчисли производната на функция? Всички тези въпроси могат да бъдат комбинирани в едно: как да се разбира производната?
Геометричен и физически смисъл на производната
Нека има функция f (x) дадени в някакъв интервал (а, б) ... Точки х и х0 принадлежат към този интервал. Когато x се промени, самата функция се променя. Промяна на аргумент - разликата между неговите стойности x-x0 ... Тази разлика е написана като делта х и се нарича инкремент на аргумента. Промяна или увеличение на функция е разликата в стойностите на функция в две точки. Производна дефиниция:
Производната на функция в дадена точка е границата на съотношението на нарастването на функцията в дадена точка към нарастването на аргумента, когато последният се стреми към нула.
В противен случай може да се напише така:
Какъв е смисълът да се намери такова ограничение? И ето какво:
производната на функцията в точка е равна на тангенса на ъгъла между оста OX и допирателната към графиката на функцията в тази точка.
Физическият смисъл на производната: производната на пътя по отношение на времето е равна на скоростта на праволинейното движение.
Всъщност още от училищните времена всеки знае, че скоростта е частен път. x = f (t) и времето T ... Средна скорост за определен период от време:
За да разберете скоростта на движение в даден момент t0 трябва да изчислите лимита:
Правило първо: извадете константа
Константата може да бъде преместена извън знака на производната. Освен това трябва да се направи. Когато решавате примери по математика, вземете като правило - ако можете да опростите израза, не забравяйте да опростите .
Пример. Нека изчислим производната:
Правило второ: производна на сумата от функции
Производната на сумата от две функции е равна на сумата от производни на тези функции. Същото важи и за производната на разликата на функциите.
Няма да даваме доказателство за тази теорема, а по -скоро ще разгледаме практически пример.
Намерете производната на функция:
Правило трето: производна на продукта на функциите
Производната на произведението на две диференцируеми функции се изчислява по формулата:
Пример: намерете производната на функция:
Решение: 
Тук е важно да се каже за изчисляването на производни на сложни функции. Производната на сложна функция е равна на произведението на производната на тази функция по отношение на междинния аргумент от производната на междинния аргумент по отношение на независимата променлива.
В горния пример срещаме израза:
В този случай междинният аргумент е 8x към петата степен. За да се изчисли производната на такъв израз, първо се изчислява производната на външната функция по отношение на междинния аргумент и след това се умножава по производната на непосредствения междинен аргумент по отношение на независимата променлива.
Четвърто правило: коефициентната производна на две функции
Формула за определяне на производната на коефициента на две функции:
Опитахме се да ви разкажем за производни за манекени от нулата. Тази тема не е толкова проста, колкото звучи, затова бъдете предупредени: в примерите често има подводни камъни, така че бъдете внимателни при изчисляването на деривати.
За всякакви въпроси по тази и други теми можете да се обърнете към студентската служба. За кратко време ще ви помогнем да решите най -трудния тест и да се справите със задачи, дори ако никога преди не сте правили изчисляване на деривати.
Производната на функция е една от трудните теми в училищната програма. Не всеки завършил ще отговори на въпроса какво е производно.
Тази статия обяснява просто и ясно какво е производно и за какво служи.... Сега няма да се стремим към математическа строгост на изложението. Най -важното е да разберете смисъла.
Нека си припомним определението:
Производната е скоростта на промяна на функцията.
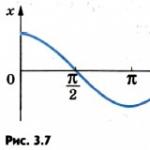
Фигурата показва графики на три функции. Кой според вас расте по -бързо?
Отговорът е очевиден - третият. Той има най -висок процент на промяна, тоест най -големият дериват.
Ето още един пример.
Костя, Гриша и Матвей получиха работа едновременно. Нека видим как доходът им се е променил през годината:
Можете да видите всичко на графиката веднага, нали? Доходът на Костя се е удвоил за шест месеца. И доходите на Гриша също се увеличиха, но леко. И доходът на Матвей падна до нула. Условията за стартиране са същите, но скоростта на промяна на функцията, т.е. производно, - различен. Що се отнася до Матвей, дериватът на неговия доход като цяло е отрицателен.
Интуитивно можем лесно да преценим скоростта на промяна на функция. Но как да го направим?
Всъщност разглеждаме колко стръмно се издига графиката на функциите (или надолу). С други думи, колко бързо се променя y с промяната на x. Очевидно една и съща функция в различни точки може да има различни стойности на производната - тоест може да се променя по -бързо или по -бавно.
Производната на функцията се обозначава.
Нека ви покажем как да го намерите с помощта на графиката.
Начертава се графика на някаква функция. Нека вземем точка с абсциса. Нека нарисуваме в този момент допирателната към графиката на функцията. Искаме да преценим колко стръмно е графика на функциите. Удобна стойност за това е тангенс на ъгъла на наклон на тангентата.
Производната на функцията в дадена точка е равна на тангенса на ъгъла на наклона на тангента, изтеглена към графиката на функцията в тази точка.
Обърнете внимание - като ъгъл на наклон на допирателната, ние приемаме ъгъла между допирателната и положителната посока на оста.
Понякога учениците питат какво е допирателна функция. Това е права линия, която има една обща точка с графиката в този раздел и както е показано на нашата фигура. Прилича на допирателна към окръжност.
Ще го намерим. Помним, че допирателната на остър ъгъл в правоъгълен триъгълник е равна на отношението на противоположния крак към съседния крак. От триъгълника:
Открихме производната с помощта на графиката, без дори да знаем формулата на функцията. Такива проблеми често се срещат на изпита по математика под номера.
Има и друга важна връзка. Припомнете си, че правата линия се дава от уравнението
Количеството в това уравнение се нарича наклон на права линия... Той е равен на тангента на ъгъла на наклон на правата линия към оста.
.
Разбираме това
Нека си припомним тази формула. Той изразява геометричното значение на производната.
Производната на функция в дадена точка е равна на наклона на допирателната, изтеглена към графиката на функцията в тази точка.
С други думи, производната е равна на тангента на ъгъла на наклон на тангента.
Вече казахме, че една и съща функция може да има различни производни в различни точки. Нека да видим как производната е свързана с поведението на функцията.
Нека начертаем графика на някаква функция. Нека тази функция се увеличава в някои области и намалява в други, и с различни темпове. И нека тази функция има максимални и минимални точки.
В един момент функцията се увеличава. Допирателна към графиката, начертана в точка, образува остър ъгъл с положителната посока на оста. Това означава, че производната е положителна в точката.
В този момент нашата функция намалява. Допирателната в тази точка образува тъп ъгъл с положителната посока на оста. Тъй като тангенсата на тъп ъгъл е отрицателна, производната в точката е отрицателна.
Ето какво се случва:
Ако функцията се увеличава, нейната производна е положителна.
Ако тя намалее, нейната производна е отрицателна.
И какво ще се случи при максималните и минималните точки? Виждаме, че в точките (максимална точка) и (минимална точка) тангентата е хоризонтална. Следователно, допирателната на ъгъла на наклон на допирателната в тези точки е нула, а производната също е нула.
Точката е максималната точка. В този момент увеличението на функцията се заменя с намаляване. Следователно знакът на производната се променя в точката от "плюс" на "минус".
В точката - минималната точка - производната също е нула, но знакът й се променя от „минус“ на „плюс“.
Заключение: с помощта на производна можете да научите всичко, което ни интересува за поведението на функция.
Ако производната е положителна, тогава функцията се увеличава.
Ако производната е отрицателна, тогава функцията намалява.
В максималната точка производната е нула и променя знака от "плюс" на "минус".
В минималната точка производната също е нула и променя знака от "минус" на "плюс".
Нека напишем тези заключения под формата на таблица:
| се увеличава | максимална точка | намалява | минимална точка | се увеличава | |
| + | 0 | - | 0 | + |
Нека направим две малки уточнения. Един от тях ще ви е необходим, когато решавате проблемите на изпита. Друг - през първата година, с по -сериозно проучване на функции и производни.
Възможен е случаят, когато производната на функция във всяка точка е равна на нула, но функцията няма максимум или минимум в тази точка. Това е т.нар :
В даден момент допирателната към графиката е хоризонтална, а производната е нула. Въпреки това, до точката функцията се увеличи - и след точката тя продължава да се увеличава. Знакът на деривата не се променя - както беше положителен, той остава.
Също така се случва, че производната не съществува в максималната или минималната точка. На графиката това съответства на рязък завой, когато допирателна в дадена точка не може да бъде изтеглена.
И как да намерим производната, ако функцията е дадена не от графика, а от формула? В този случай,
Абсолютно невъзможно е да се решават физически задачи или примери в математиката без познаване на производната и методите за нейното изчисляване. Производната е една от най -важните концепции на математическия анализ. Решихме да посветим днешната статия на тази фундаментална тема. Какво е производна, какъв е нейният физически и геометричен смисъл, как да се изчисли производната на функция? Всички тези въпроси могат да бъдат комбинирани в едно: как да се разбира производната?
Геометричен и физически смисъл на производната
Нека има функция f (x) дадени в някакъв интервал (а, б) ... Точки х и х0 принадлежат към този интервал. Когато x се промени, самата функция се променя. Промяна на аргумент - разликата между неговите стойности x-x0 ... Тази разлика е написана като делта х и се нарича инкремент на аргумента. Промяна или увеличение на функция е разликата в стойностите на функция в две точки. Производна дефиниция:
Производната на функция в дадена точка е границата на съотношението на нарастването на функцията в дадена точка към нарастването на аргумента, когато последният се стреми към нула.
В противен случай може да се напише така:
Какъв е смисълът да се намери такова ограничение? И ето какво:
производната на функцията в точка е равна на тангенса на ъгъла между оста OX и допирателната към графиката на функцията в тази точка.
Физическият смисъл на производната: производната на пътя по отношение на времето е равна на скоростта на праволинейното движение.
Всъщност още от училищните времена всеки знае, че скоростта е частен път. x = f (t) и времето T ... Средна скорост за определен период от време:
За да разберете скоростта на движение в даден момент t0 трябва да изчислите лимита:
Правило първо: извадете константа
Константата може да бъде преместена извън знака на производната. Освен това трябва да се направи. Когато решавате примери по математика, вземете като правило - ако можете да опростите израза, не забравяйте да опростите .
Пример. Нека изчислим производната:
Правило второ: производна на сумата от функции
Производната на сумата от две функции е равна на сумата от производни на тези функции. Същото важи и за производната на разликата на функциите.
Няма да даваме доказателство за тази теорема, а по -скоро ще разгледаме практически пример.
Намерете производната на функция:
Правило трето: производна на продукта на функциите
Производната на произведението на две диференцируеми функции се изчислява по формулата:
Пример: намерете производната на функция:
Решение:
Тук е важно да се каже за изчисляването на производни на сложни функции. Производната на сложна функция е равна на произведението на производната на тази функция по отношение на междинния аргумент от производната на междинния аргумент по отношение на независимата променлива.
В горния пример срещаме израза:
В този случай междинният аргумент е 8x към петата степен. За да се изчисли производната на такъв израз, първо се изчислява производната на външната функция по отношение на междинния аргумент и след това се умножава по производната на непосредствения междинен аргумент по отношение на независимата променлива.
Четвърто правило: коефициентната производна на две функции
Формула за определяне на производната на коефициента на две функции:
Опитахме се да ви разкажем за производни за манекени от нулата. Тази тема не е толкова проста, колкото звучи, затова бъдете предупредени: в примерите често има подводни камъни, така че бъдете внимателни при изчисляването на деривати.
За всякакви въпроси по тази и други теми можете да се обърнете към студентската служба. За кратко време ще ви помогнем да решите най -трудния тест и да се справите със задачи, дори ако никога преди не сте правили изчисляване на деривати.
Може да се извърши за знака производно:
(af (x) "= af" (x).
Например:
Производна на алгебрична суманяколко функции (взети в непроменено число) е равно на алгебричната сума на техните деривати:
(f 1 (x) + f 2 (x) - f 3 (x)) "= f 1" (x) + f 2 "(x) - f 3" (x).
Например:
(0,3 x 2 - 2 x + 0,8) "= (0,3 x 2)" - (2 x) " + (0,8)" = 0,6 x - 2 ( производноПоследният срокуравнението е равно на нула).
Ако производна на функция g е ненулева, тогава съотношението f / g също има краен дериват... Това свойство може да бъде записано като:
.
Нека бъде функции y = f (x) и y = g (x) имат крайни производнив точката x 0. Тогава функции f ± g и f g също имат крайни производни втова точка... Тогава получаваме:
(f ± g) ′ = f ′ ± g ′,
(f g) ′ = f ′ g + f g ′.
Производна на сложна функция.
Нека бъде функция y = f (x) има крайната производна в точката x 0, функцията z = s (y) има крайна производна в точката y 0 = f (x 0).
Тогава сложна функция z = s (f (x)) също има крайна производна в тази точка. Горното може да бъде написано като:
.
Производна на обратната функция.
Нека функцията y = f (x) има обратна функция x = g (y) върху някои интервал(a, b) и има ненулева краен дериватна тази функция в точката x 0, която принадлежи на области на дефиниция, т.е. x 0 ∈ (a, b).
Тогава обратна функцияТо има производнов точката y 0 = f (x 0):
.
Производна на неявна функция.
Ако функция y = f (x) имплицитно уравнение F (x, y (x)) = 0, тогава неговото производносе намира от условието:
.
Казват, че функция y = f (x) неявно уточнено, Ако тя идентичноудовлетворява съотношението:
където F (x, y) е някаква функция от два аргумента.
Производна на параметрично определена функция.
Ако функция y = f (x) е дадено параметрично, като се използва разглежданото
