Днес, приятели, няма да има сополи и сантименти. Вместо това ще ви изпратя в битка с един от най-страшните противници в курса по алгебра за 8-9 клас без допълнителни въпроси.
Да, разбрахте всичко правилно: говорим за неравенства с модул. Ще разгледаме четири основни техники, с които ще се научите да решавате около 90% от тези проблеми. Ами останалите 10%? Е, ще говорим за тях в отделен урок. :)
Въпреки това, преди да анализирам трикове там, бих искал да припомня два факта, които вече трябва да знаете. В противен случай рискувате изобщо да не разберете материала от днешния урок.
Това, което вече трябва да знаете
Captain Evidence, така да се каже, намеква, че за да решавате неравенства с модул, трябва да знаете две неща:
- Как се решават неравенствата?
- Какво е модул.
Да започнем с втората точка.
Дефиниция на модула
Тук всичко е просто. Има две дефиниции: алгебрична и графична. Да започнем с алгебрата:
Определение. Модулът на числото $x$ е или самото число, ако е неотрицателно, или противоположното му число, ако първоначалният $x$ все още е отрицателен.
Написано е така:
\[\ляво| x \right|=\left\( \begin(align) & x,\ x\ge 0, \\ & -x,\ x \lt 0. \\\end(align) \right.\]
говорене обикновен език, модулът е "число без минус". И именно в тази двойственост (някъде не е нужно да правите нищо с оригиналния номер, но някъде трябва да премахнете някакъв минус там) и цялата трудност за начинаещите ученици се крие.
Има и геометрична дефиниция. Също така е полезно да го знаете, но ще се позоваваме на него само в сложни и някои специални случаи, където геометричният подход е по-удобен от алгебричния (спойлер: не днес).
Определение. Нека точката $a$ е отбелязана на реалната права. След това модулът $\left| x-a \right|$ е разстоянието от точката $x$ до точката $a$ на тази права.
Ако нарисувате картина, ще получите нещо подобно:
 Дефиниране на графичен модул
Дефиниране на графичен модул По един или друг начин, ключовото му свойство веднага следва от дефиницията на модула: модулът на числото винаги е неотрицателна стойност. Този факт ще бъде червена нишка през цялата ни история днес.
Решение на неравенства. Метод на разстояние
Сега нека се заемем с неравенствата. Има много от тях, но нашата задача сега е да можем да решим поне най-простия от тях. Тези, които се свеждат до линейни неравенства, както и до метода на интервалите.
Имам два големи урока по тази тема (между другото, много, МНОГО полезни - препоръчвам изучаване):
- Интервалният метод за неравенства (особено гледайте видеото);
- Дробно-рационални неравенства е много обемен урок, но след него изобщо няма да ви останат въпроси.
Ако знаете всичко това, ако фразата „да преминем от неравенство към уравнение“ не ви кара смътно да искате да се убиете в стената, значи сте готови: добре дошли в ада в основната тема на урока. :)
1. Неравенства от формата "Модул по-малък от функция"
Това е една от най-често срещаните задачи с модули. Необходимо е да се реши неравенство от вида:
\[\ляво| f\надясно| \ltg\]
Всичко може да действа като функции $f$ и $g$, но обикновено те са полиноми. Примери за такива неравенства:
\[\begin(align) & \left| 2x+3\надясно| \ltx+7; \\ & \left| ((x)^(2))+2x-3 \right|+3\left(x+1 \right) \lt 0; \\ & \left| ((x)^(2))-2\left| x \right|-3 \right| \lt 2. \\\край (подравняване)\]
Всички те се решават буквално в един ред според схемата:
\[\ляво| f\надясно| \lt g\Rightarrow -g \lt f \lt g\quad \left(\Rightarrow \left\( \begin(align) & f \lt g, \\ & f \gt -g \\\end(align) \право.\право)\]
Лесно се вижда, че се отърваваме от модула, но вместо това получаваме двойно неравенство (или, което е същото, система от две неравенства). Но този преход отчита абсолютно всички възможни проблеми: ако числото под модула е положително, методът работи; ако е отрицателен, той все още работи; и дори с най-неадекватната функция на мястото на $f$ или $g$, методът пак ще работи.
Естествено възниква въпросът: не е ли по-лесно? За съжаление не можете. Това е целият смисъл на модула.
Но стига с философстването. Нека разрешим няколко проблема:
Задача. Решете неравенството:
\[\ляво| 2x+3\надясно| \ltx+7\]
Решение. И така, имаме класическо неравенство от формата „модулът е по-малък от“ - дори няма какво да се трансформира. Ние работим по алгоритъма:
\[\begin(align) & \left| f\надясно| \lt g\Стрелка надясно -g \lt f \lt g; \\ & \left| 2x+3\надясно| \lt x+7\Стрелка надясно -\left(x+7 \right) \lt 2x+3 \lt x+7 \\\end(align)\]
Не бързайте да отваряте скобите, предшествани от „минус“: напълно възможно е поради бързината да направите обидна грешка.
\[-x-7 \lt 2x+3 \lt x+7\]
\[\left\( \begin(align) & -x-7 \lt 2x+3 \\ & 2x+3 \lt x+7 \\ \end(align) \right.\]
\[\left\( \begin(align) & -3x \lt 10 \\ & x \lt 4 \\ \end(align) \right.\]
\[\left\( \begin(align) & x \gt -\frac(10)(3) \\ & x \lt 4 \\ \end(align) \right.\]
Задачата е сведена до две елементарни неравенства. Отбелязваме техните решения на успоредни реални прави:
Пресечна точка на много
Пресечната точка на тези множества ще бъде отговорът.
Отговор: $x\in \left(-\frac(10)(3);4 \right)$
Задача. Решете неравенството:
\[\ляво| ((x)^(2))+2x-3 \right|+3\left(x+1 \right) \lt 0\]
Решение. Тази задача е малко по-трудна. Като начало изолираме модула, като преместим втория член вдясно:
\[\ляво| ((x)^(2))+2x-3 \right| \lt -3\наляво(x+1 \надясно)\]
Очевидно отново имаме неравенство от формата „модулът е по-малък“, така че се отърваваме от модула според вече известния алгоритъм:
\[-\left(-3\left(x+1 \right) \right) \lt ((x)^(2))+2x-3 \lt -3\left(x+1 \right)\]
Сега внимание: някой ще каже, че съм малко перверзник с всички тези скоби. Но още веднъж напомням, че основната ни цел е решете правилно неравенството и получете отговора. По-късно, когато сте усвоили перфектно всичко, което е описано в този урок, можете да се изопачавате както искате: отваряйте скоби, добавяйте минуси и т.н.
И като за начало, просто се отърваваме от двойното минус отляво:
\[-\left(-3\left(x+1 \right) \right)=\left(-1 \right)\cdot \left(-3 \right)\cdot \left(x+1 \right) =3\ляво(x+1\дясно)\]
Сега нека отворим всички скоби в двойното неравенство:
Да преминем към двойното неравенство. Този път изчисленията ще бъдат по-сериозни:
\[\left\( \begin(align) & ((x)^(2))+2x-3 \lt -3x-3 \\ & 3x+3 \lt ((x)^(2))+2x -3 \\ \end(align) \right.\]
\[\left\( \begin(align) & ((x)^(2))+5x \lt 0 \\ & ((x)^(2))-x-6 \gt 0 \\ \end( подравняване)\надясно.\]
И двете неравенства са квадратни и се решават по интервалния метод (затова казвам: ако не знаете какво е, по-добре още не се захващайте с модули). Преминаваме към уравнението в първото неравенство:
\[\begin(align) & ((x)^(2))+5x=0; \\ & x\left(x+5 \right)=0; \\ & ((x)_(1))=0;((x)_(2))=-5. \\\край (подравняване)\]
Както можете да видите, резултатът се оказа непълно квадратно уравнение, което се решава елементарно. Сега да разгледаме второто неравенство на системата. Там трябва да приложите теоремата на Виета:
\[\begin(align) & ((x)^(2))-x-6=0; \\ & \left(x-3 \right)\left(x+2 \right)=0; \\& ((x)_(1))=3;((x)_(2))=-2. \\\край (подравняване)\]
Отбелязваме получените числа на две успоредни линии (отделно за първото неравенство и отделно за второто):
Отново, тъй като решаваме система от неравенства, ние се интересуваме от пресечната точка на защрихованите множества: $x\in \left(-5;-2 \right)$. Това е отговорът.
Отговор: $x\in \left(-5;-2 \right)$
Мисля, че след тези примери схемата за решение е много ясна:
- Изолирайте модула, като преместите всички други членове в противоположната страна на неравенството. Така получаваме неравенство от вида $\left| f\надясно| \ltg$.
- Решете това неравенство, като се отървете от модула, както е описано по-горе. В един момент ще е необходимо да се премине от двойно неравенство към система от два независими израза, всеки от които вече може да бъде решен отделно.
- Накрая остава само да пресечем решенията на тези два независими израза - и това е, ще получим окончателния отговор.
Подобен алгоритъм съществува за неравенства от следния тип, когато модулът е по-голям от функцията. Има обаче няколко сериозни "но". За тези „но“ ще говорим сега.
2. Неравенства от формата "Модулът е по-голям от функцията"
Те изглеждат така:
\[\ляво| f\надясно| \gt g\]
Подобен на предишния? Изглежда. Въпреки това, такива задачи се решават по съвсем различен начин. Формално схемата е следната:
\[\ляво| f\надясно| \gt g\Rightarrow \left[ \begin(align) & f \gt g, \\ & f \lt -g \\\end(align) \right.\]
С други думи, разглеждаме два случая:
- Първо, просто игнорираме модула - решаваме обичайното неравенство;
- Тогава всъщност отваряме модула със знака минус и след това умножаваме двете части на неравенството по −1 със знак.
В този случай опциите се комбинират с квадратна скоба, т.е. Имаме комбинация от две изисквания.
Обърнете внимание отново: пред нас не е система, а агрегат, следователно в отговора множествата се комбинират, а не се пресичат. Това е фундаментална разлика от предишния параграф!
Като цяло, много студенти имат много объркване със съюзите и пресичанията, така че нека разгледаме този въпрос веднъж завинаги:
- "∪" е знак за конкатенация. Всъщност това е стилизирана буква "U", която дойде при нас от на английски езики е съкращение от "Съюз", т.е. „Асоциации“.
- „∩“ е знакът за пресичане. Тези глупости не са дошли от никъде, а просто се появяват като опозиция на "∪".
За да го направите още по-лесно за запомняне, просто добавете крака към тези знаци, за да направите очила (само не ме обвинявайте сега, че насърчавам наркоманията и алкохолизма: ако изучавате сериозно този урок, значи вече сте наркоман):
 Разлика между пресичане и обединение на множества
Разлика между пресичане и обединение на множества Преведено на руски това означава следното: съюзът (колекцията) включва елементи от двата набора, следователно не по-малко от всеки от тях; но пресечната точка (системата) включва само тези елементи, които са както в първото множество, така и във второто. Следователно пресечната точка на наборите никога не е по-голяма от наборите източник.
Значи стана по-ясно? Това е страхотно. Да преминем към практиката.
Задача. Решете неравенството:
\[\ляво| 3x+1 \надясно| \gt 5-4x\]
Решение. Ние действаме по схемата:
\[\ляво| 3x+1 \надясно| \gt 5-4x\дясна стрелка \left[ \begin(align) & 3x+1 \gt 5-4x \\ & 3x+1 \lt -\left(5-4x \right) \\\end(align) \ точно.\]
Решаваме всяко неравенство на населението:
\[\left[ \begin(align) & 3x+4x \gt 5-1 \\ & 3x-4x \lt -5-1 \\ \end(align) \right.\]
\[\left[ \begin(align) & 7x \gt 4 \\ & -x \lt -6 \\ \end(align) \right.\]
\[\left[ \begin(align) & x \gt 4/7\ \\ & x \gt 6 \\ \end(align) \right.\]
Маркираме всеки получен набор на числовата линия и след това ги комбинираме:
Обединение на комплекти
Очевидно отговорът е $x\in \left(\frac(4)(7);+\infty \right)$
Отговор: $x\in \left(\frac(4)(7);+\infty \right)$
Задача. Решете неравенството:
\[\ляво| ((x)^(2))+2x-3 \right| \gtx\]
Решение. Добре? Не, всичко е едно и също. Преминаваме от неравенство с модул към набор от две неравенства:
\[\ляво| ((x)^(2))+2x-3 \right| \gt x\Rightarrow \left[ \begin(align) & ((x)^(2))+2x-3 \gt x \\ & ((x)^(2))+2x-3 \lt -x \\\end(align) \right.\]
Решаваме всяко неравенство. За съжаление, корените няма да са много добри там:
\[\begin(align) & ((x)^(2))+2x-3 \gt x; \\ & ((x)^(2))+x-3 \gt 0; \\ &D=1+12=13; \\ & x=\frac(-1\pm \sqrt(13))(2). \\\край (подравняване)\]
Във второто неравенство също има малко игра:
\[\begin(align) & ((x)^(2))+2x-3 \lt -x; \\ & ((x)^(2))+3x-3 \lt 0; \\ &D=9+12=21; \\ & x=\frac(-3\pm \sqrt(21))(2). \\\край (подравняване)\]
Сега трябва да отбележим тези числа на две оси - по една ос за всяко неравенство. Трябва обаче да маркирате точките в правилния ред: колкото по-голямо е числото, толкова повече се измества точката надясно.
И тук чакаме настройка. Ако всичко е ясно с числата $\frac(-3-\sqrt(21))(2) \lt \frac(-1-\sqrt(13))(2)$ (членовете в числителя на първия част са по-малки от членовете в числителя на секундата, така че сумата също е по-малка), с числата $\frac(-3-\sqrt(13))(2) \lt \frac(-1+\sqrt (21))(2)$ също няма да има трудности (положително число очевидно е по-отрицателно), но с последната двойка всичко не е толкова просто. Кое е по-голямо: $\frac(-3+\sqrt(21))(2)$ или $\frac(-1+\sqrt(13))(2)$? От отговора на този въпрос ще зависи разположението на точките на числовите прави и всъщност отговорът.
Така че нека сравним:
\[\begin(matrix) \frac(-1+\sqrt(13))(2)\vee \frac(-3+\sqrt(21))(2) \\ -1+\sqrt(13)\ vee -3+\sqrt(21) \\ 2+\sqrt(13)\vee \sqrt(21) \\\end(matrix)\]
Изолирахме корена, получихме неотрицателни числа от двете страни на неравенството, така че имаме право да поставим на квадрат и двете страни:
\[\begin(matrix) ((\left(2+\sqrt(13) \right))^(2))\vee ((\left(\sqrt(21) \right))^(2)) \ \4+4\sqrt(13)+13\vee 21 \\ 4\sqrt(13)\vee 3 \\\end(matrix)\]
Мисля, че е безсмислено, че $4\sqrt(13) \gt 3$, така че $\frac(-1+\sqrt(13))(2) \gt \frac(-3+\sqrt(21)) ( 2)$, накрая точките на осите ще бъдат подредени по следния начин:
Случай на грозни корени
Нека ви напомня, че решаваме множество, така че отговорът ще бъде обединението, а не пресечната точка на защрихованите множества.
Отговор: $x\in \left(-\infty ;\frac(-3+\sqrt(21))(2) \right)\bigcup \left(\frac(-1+\sqrt(13))(2 );+\infty\right)$
Както можете да видите, нашата схема работи чудесно както за прости задачи, така и за много трудни. Единственото нещо " слабост„При този подход трябва компетентно да сравнявате ирационални числа (и повярвайте ми: това не са само корени). Но отделен (и много сериозен урок) ще бъде посветен на въпросите на сравнението. И продължаваме напред.
3. Неравенства с неотрицателни "опашки"
Така стигнахме до най-интересното. Това са неравенства от вида:
\[\ляво| f\надясно| \gt\наляво| g\надясно|\]
Най-общо казано, алгоритъмът, за който ще говорим сега, е верен само за модула. Работи във всички неравенства, където има гарантирани неотрицателни изрази отляво и отдясно:
Какво да правим с тези задачи? Просто запомни:
В неравенства с неотрицателни опашки и двете страни могат да бъдат повдигнати на всяка естествена степен. Няма да има допълнителни ограничения.
На първо място, ще се интересуваме от квадратурата - тя изгаря модули и корени:
\[\begin(align) & ((\left(\left| f \right| \right))^(2))=((f)^(2)); \\ & ((\left(\sqrt(f) \right))^(2))=f. \\\край (подравняване)\]
Просто не бъркайте това с вземане на корен на квадрат:
\[\sqrt(((f)^(2)))=\left| f \right|\ne f\]
Безброй грешки бяха направени, когато ученик забрави да инсталира модул! Но това е съвсем различна история (това са, така да се каже, ирационални уравнения), така че няма да навлизаме в нея сега. Нека по-добре да разрешим няколко проблема:
Задача. Решете неравенството:
\[\ляво| x+2 \right|\ge \left| 1-2x \right|\]
Решение. Веднага забелязваме две неща:
- Това е нестрого неравенство. Точките на числовата ос ще бъдат изчертани.
- И двете страни на неравенството очевидно са неотрицателни (това е свойство на модула: $\left| f\left(x \right) \right|\ge 0$).
Следователно можем да повдигнем на квадрат двете страни на неравенството, за да се отървем от модула и да решим проблема, използвайки обичайния метод на интервала:
\[\begin(align) & ((\left(\left| x+2 \right| \right))^(2))\ge ((\left(\left| 1-2x \right| \right) )^(2)); \\ & ((\left(x+2 \right))^(2))\ge ((\left(2x-1 \right))^(2)). \\\край (подравняване)\]
На последната стъпка изневерих малко: промених последователността от членове, използвайки четността на модула (всъщност умножих израза $1-2x$ по −1).
\[\begin(align) & ((\left(2x-1 \right))^(2))-((\left(x+2 \right))^(2))\le 0; \\ & \left(\left(2x-1 \right)-\left(x+2 \right) \right)\cdot \left(\left(2x-1 \right)+\left(x+2 \ дясно)\дясно)\le 0; \\ & \left(2x-1-x-2 \right)\cdot \left(2x-1+x+2 \right)\le 0; \\ & \left(x-3 \right)\cdot \left(3x+1 \right)\le 0. \\\end(align)\]
Решаваме по интервалния метод. Нека преминем от неравенство към уравнение:
\[\begin(align) & \left(x-3 \right)\left(3x+1 \right)=0; \\ & ((x)_(1))=3;((x)_(2))=-\frac(1)(3). \\\край (подравняване)\]
Отбелязваме намерените корени на числовата ос. Още веднъж: всички точки са защриховани, защото първоначалното неравенство не е строго!
Отървете се от знака на модула
Нека ви напомня за особено упоритите: вземаме знаците от последното неравенство, което беше написано преди да преминем към уравнението. И рисуваме върху площите, изисквани в същото неравенство. В нашия случай това е $\left(x-3 \right)\left(3x+1 \right)\le 0$.
Добре, всичко свърши. Проблема решен.
Отговор: $x\in \left[ -\frac(1)(3);3 \right]$.
Задача. Решете неравенството:
\[\ляво| ((x)^(2))+x+1 \right|\le \left| ((x)^(2))+3x+4 \right|\]
Решение. Правим всичко по същия начин. Няма да коментирам - просто вижте последователността на действията.
Нека го повдигнем на квадрат:
\[\begin(align) & ((\left(\left| ((x)^(2))+x+1 \right| \right))^(2))\le ((\left(\left | ((x)^(2))+3x+4 \right| \right))^(2)); \\ & ((\left(((x)^(2))+x+1 \right))^(2))\le ((\left(((x)^(2))+3x+4 \десен))^(2)); \\ & ((\left(((x)^(2))+x+1 \right))^(2))-((\left(((x)^(2))+3x+4 \ надясно))^(2))\le 0; \\ & \left(((x)^(2))+x+1-((x)^(2))-3x-4 \right)\times \\ & \times \left(((x) ^(2))+x+1+((x)^(2))+3x+4 \right)\le 0; \\ & \left(-2x-3 \right)\left(2((x)^(2))+4x+5 \right)\le 0. \\\end(align)\]
Метод на разстояние:
\[\begin(align) & \left(-2x-3 \right)\left(2((x)^(2))+4x+5 \right)=0 \\ & -2x-3=0\ Стрелка надясно x=-1.5; \\ & 2((x)^(2))+4x+5=0\Стрелка надясно D=16-40 \lt 0\Стрелка надясно \varnothing . \\\край (подравняване)\]
На числовата ос има само един корен:
Отговорът е цяла гама
Отговор: $x\in \left[ -1.5;+\infty \right)$.
Малка забележка за последната задача. Както един от моите ученици точно отбеляза, и двата подмодулни израза в това неравенство са очевидно положителни, така че знакът за модул може да бъде пропуснат без вреда за здравето.
Но това вече е съвсем друго ниво на мислене и друг подход – условно може да се нарече метод на следствията. За него - в отделен урок. А сега нека да преминем към последната част на днешния урок и да разгледаме един универсален алгоритъм, който винаги работи. Дори когато всички предишни подходи бяха безсилни. :)
4. Метод на изброяване на опциите
Ами ако всички тези трикове не работят? Ако неравенството не се свежда до неотрицателни опашки, ако е невъзможно да се изолира модулът, ако изобщо болка-тъга-копнеж?
Тогава на сцената излиза "тежката артилерия" на цялата математика - методът на изброяването. По отношение на неравенствата с модула изглежда така:
- Изпишете всички подмодулни изрази и ги приравнете към нула;
- Решете получените уравнения и отбележете намерените корени на една числова ос;
- Правата линия ще бъде разделена на няколко секции, в рамките на които всеки модул има фиксиран знак и следователно недвусмислено се разширява;
- Решете неравенството на всеки такъв участък (можете отделно да разгледате граничните корени, получени в параграф 2 - за надеждност). Комбинирайте резултатите - това ще бъде отговорът. :)
Е, как? слаб? Лесно! Само за дълго време. Да видим на практика:
Задача. Решете неравенството:
\[\ляво| x+2 \надясно| \lt\наляво| x-1 \right|+x-\frac(3)(2)\]
Решение. Тези глупости не се свеждат до неравенства като $\left| f\надясно| \lt g$, $\left| f\надясно| \gt g$ или $\left| f\надясно| \lt\ляво| g \right|$, така че да продължим.
Изписваме подмодулни изрази, приравняваме ги към нула и намираме корените:
\[\begin(align) & x+2=0\Rightarrow x=-2; \\ & x-1=0\Стрелка надясно x=1. \\\край (подравняване)\]
Общо имаме два корена, които разделят числовата линия на три секции, вътре в които всеки модул се разкрива уникално:
Разделяне на числовата ос с нули на субмодулни функции
Нека разгледаме всеки раздел поотделно.
1. Нека $x \lt -2$. Тогава и двата израза на подмодула са отрицателни и оригиналното неравенство се пренаписва, както следва:
\[\begin(align) & -\left(x+2 \right) \lt -\left(x-1 \right)+x-1,5 \\ & -x-2 \lt -x+1+ x-1,5 \\ & x \gt 1,5 \\\end(align)\]
Имаме доста просто ограничение. Нека го пресечем с първоначалното предположение, че $x \lt -2$:
\[\left\( \begin(align) & x \lt -2 \\ & x \gt 1,5 \\\end(align) \right.\Rightarrow x\in \varnothing \]
Очевидно променливата $x$ не може едновременно да бъде по-малка от −2, но по-голяма от 1,5. В тази област няма решения.
1.1. Нека отделно разгледаме граничния случай: $x=-2$. Нека просто заместим това число в първоначалното неравенство и да проверим: важи ли?
\[\begin(align) & ((\left. \left| x+2 \right| \lt \left| x-1 \right|+x-1,5 \right|)_(x=-2) ) \\ & 0 \lt \left| -3 \right|-2-1.5; \\ & 0 \lt 3-3,5; \\ & 0 \lt -0,5\Стрелка надясно \varnothing . \\\край (подравняване)\]
Очевидно веригата от изчисления ни е довела до грешното неравенство. Следователно първоначалното неравенство също е невярно и $x=-2$ не е включено в отговора.
2. Сега нека $-2 \lt x \lt 1$. Левият модул вече ще се отвори с "плюс", но десният все още е с "минус". Ние имаме:
\[\begin(align) & x+2 \lt -\left(x-1 \right)+x-1.5 \\ & x+2 \lt -x+1+x-1.5 \\& x \lt - 2.5 \\\край (подравняване)\]
Отново се пресичаме с първоначалното изискване:
\[\left\( \begin(align) & x \lt -2,5 \\ & -2 \lt x \lt 1 \\\end(align) \right.\Rightarrow x\in \varnothing \]
И отново празното множество от решения, тъй като няма числа, които да са едновременно по-малки от −2,5 и по-големи от −2.
2.1. И отново специален случай: $x=1$. Заменяме в първоначалното неравенство:
\[\begin(align) & ((\left. \left| x+2 \right| \lt \left| x-1 \right|+x-1,5 \right|)_(x=1)) \\ & \left| 3\надясно| \lt\наляво| 0 \right|+1-1.5; \\ & 3 \lt -0,5; \\ & 3 \lt -0,5\Стрелка надясно \varnothing . \\\край (подравняване)\]
Подобно на предишния „специален случай“, числото $x=1$ очевидно не е включено в отговора.
3. Последната част от реда: $x \gt 1$. Тук всички модули са разширени със знак плюс:
\[\begin(align) & x+2 \lt x-1+x-1.5 \\ & x+2 \lt x-1+x-1.5 \\ & x \gt 4.5 \\ \end(align)\ ]
И отново пресичаме намереното множество с оригиналното ограничение:
\[\left\( \begin(align) & x \gt 4,5 \\ & x \gt 1 \\\end(align) \right.\Rightarrow x\in \left(4,5;+\infty \вдясно)\]
Най-накрая! Намерихме интервала, който ще бъде отговорът.
Отговор: $x\in \left(4,5;+\infty \right)$
И накрая, една бележка, която може да ви спаси от глупави грешки при решаването на реални проблеми:
Решенията на неравенства с модули обикновено са непрекъснати множества на числовата ос - интервали и отсечки. Много по-рядко изолирани точки. И още по-рядко се случва границите на решението (края на сегмента) да съвпадат с границата на разглеждания диапазон.
Следователно, ако границите (тези много „специални случаи“) не са включени в отговора, тогава областите отляво-вдясно на тези граници почти сигурно също няма да бъдат включени в отговора. И обратното: границата, въведена в отговор, което означава, че някои области около нея също ще бъдат отговори.
Имайте това предвид, когато проверявате вашите решения.
РАЗГЛЕЖДАН
Меморандум за разбирателство на педагогическия съвет
"ОУ Зашижма"
Протокол №1
ДОГОВОРЕНО
Заместник-директор по УВР
_______ /Сидоркина Р.Л./
ОДОБРЯВАМ
Главен учител:
А. П. Конаков
Заповед №63
Решаване на уравнения и неравенства с модул
Програмата беше съставена от:
висш учител по математика
Сидоркина Р.Л.
с. Зашижемье, 2014 г
Съдържание
Въведение………………………………………………………………………3
Най-простите уравнения и неравенства с модул……………………5
Графично решаване на уравнения и неравенства с модула………….8
Други начини за решаване на уравнения и неравенства с модула……......10
Заключение ………………………………………………………………..16
Използвана литература………………………………………………………………18
Въведение
Концепцията за абсолютна стойност (модул) е една от най-важните характеристики на числото както в областта на реалните, така и в областта на комплексните числа.
Тази концепция се използва широко не само в различни раздели на училищния курс по математика, но и в курсовете по висша математика, физика и технически науки, изучавани в университетите. Например в теорията на приблизителните изчисления се използват понятията за абсолютни и относителни грешки на приблизително число. В механиката и геометрията се изучават понятията вектор и неговата дължина (векторен модул). В математическия анализ концепцията за абсолютната стойност на числото се съдържа в дефинициите на такива основни понятия като граница, ограничена функция и т.н. Проблеми, свързани с абсолютни стойности, често се срещат на математически олимпиади, приемни изпити в университети и Единния държавен изпит.И така за нас стана важно да проучим някои аспекти на тази тема.
У дома целв нашата работа е да учим различни методирешения на уравнения и неравенства с модули.
Тази целтрябва да се постигне чрез решаване на следното задачи:
Разгледайте дефиницията и някои свойства на модула.
Овладейте решението на най-простите уравнения и неравенства с модула чрез еквивалентни преходи
Разгледайте различни методи за решаване на уравнения и неравенства с модул.
обектизследвания са някои видове уравнения и неравенства с модул.
Предметизследвания - различни методи за решаване на уравнения и неравенства с модул, а именно: графичен метод, метод на геометрична интерпретация, използване на идентичност, приложение на теоремата за знаците, метод на преход към следствие, метод на интервали, метод на умножение с положителен фактор, метод на разширяване на модули.
В хода на изследването се използват методи като изучаване на литературата по този проблеми практически метод.
В хода на нашата работа проучихме източници като:
1. "Голяма математическа енциклопедия" за ученици и студенти;
Математика. УПОТРЕБА - 2011-2012г. Стандартни опции за изпит. / Под редакцията на A.L. Семенова, И.В. Ященко.
Енциклопедия "Аз познавам света" Математика;
;
Най-простите уравнения и неравенства с модул
Ще отнесем към най-простите уравнения уравненията, решени чрез един от следните еквивалентни преходи: 
Примери за решаване на най-простите уравнения.
Пример 1 Нека решим уравнението  .
.
Решение.
Отговор.  .
.
Пример 2 Нека решим уравнението.
Решение.
Отговор.  .
.
Пример 3 Нека решим уравнението  .
.
Решение.

Отговор.  .
.
Редица уравнения се решават с помощта на следната теорема.
Теорема.4 Сумата на модулите е равна на алгебричната сума на подмодулните величини тогава и само ако всяка величина има знака, с който влиза в алгебричната сума.
Пример 5 реши уравнението
Решение.Тъй като , имаме равенство на формата , където  ,
,  . Следователно първоначалното уравнение е еквивалентно на системата:
. Следователно първоначалното уравнение е еквивалентно на системата:

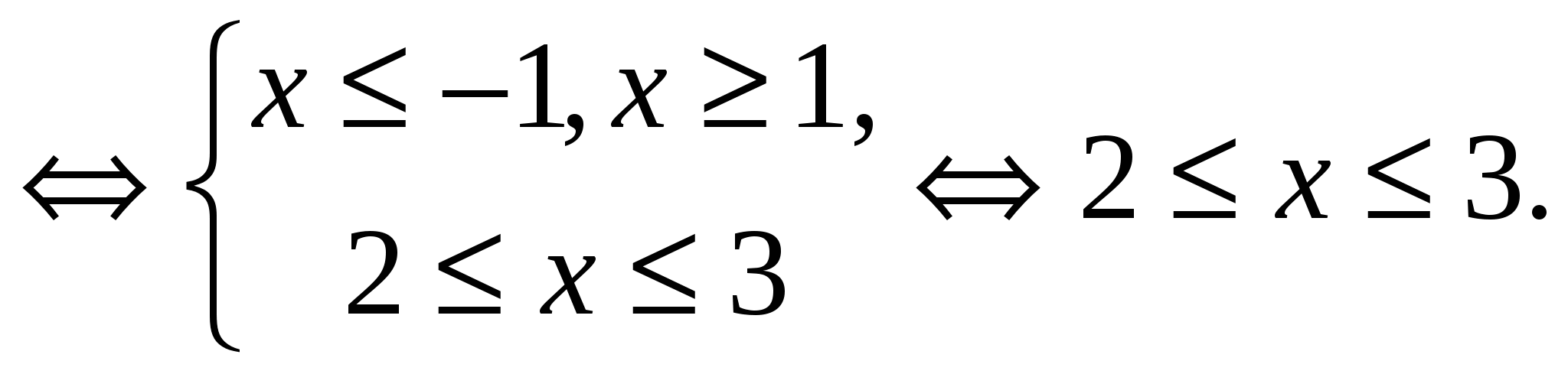
Отговор.  .
.
Примери за решаване на най-простите неравенства.
Пример 6 Нека решим неравенството  .
.
Решение.
Отговор. 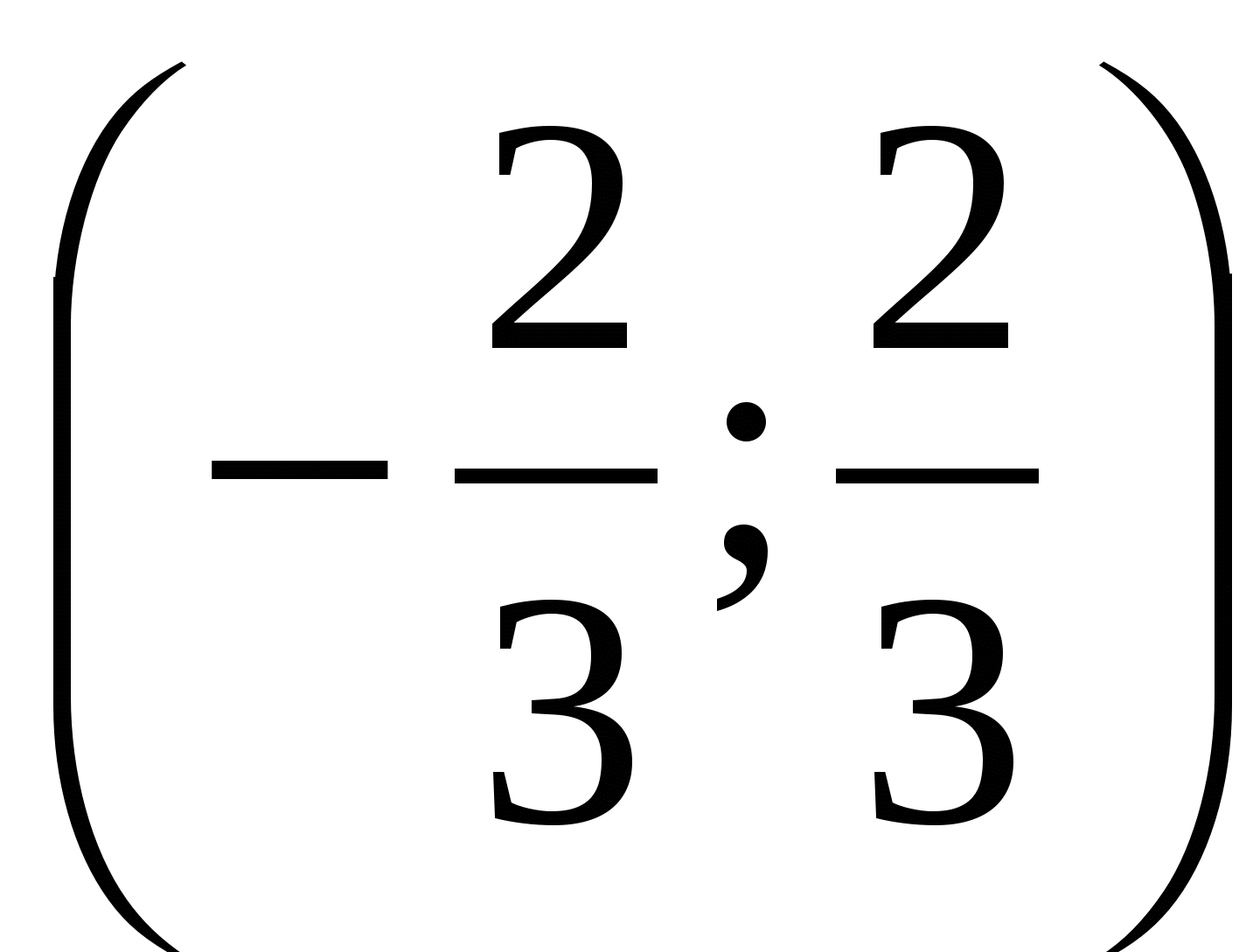 .
.
Пример 7 Нека решим неравенството  .
.
Решение.
Отговор.  .
.
Колкото и да е странно, но 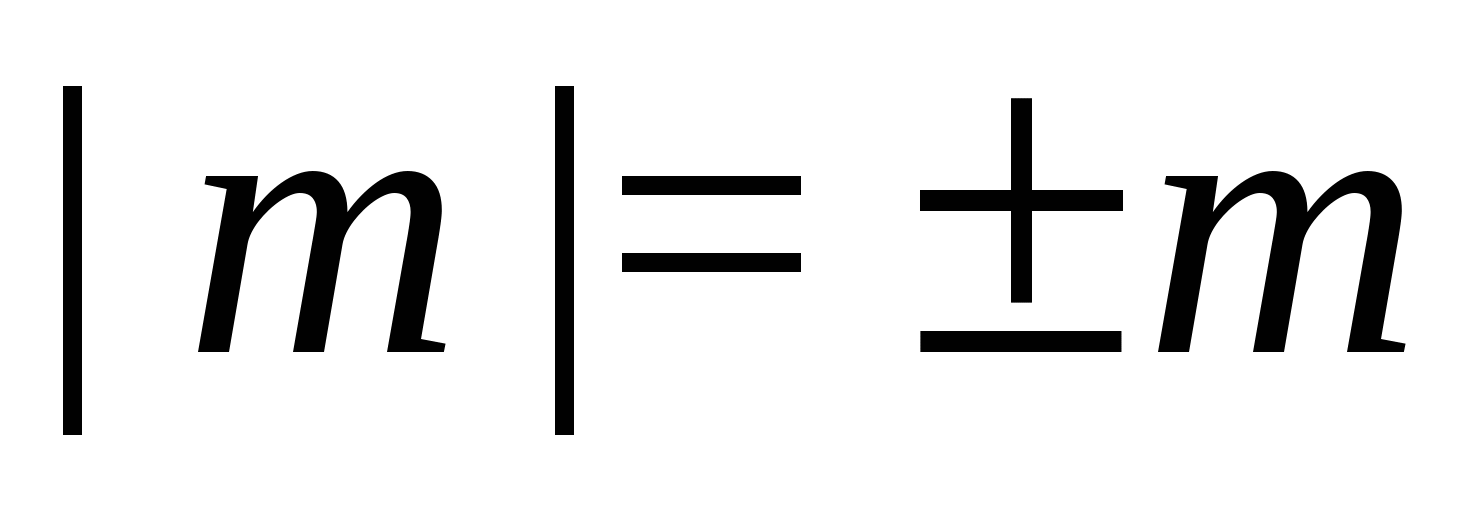 достатъчно, за да се отървете от знака модул във всички неравенства.
достатъчно, за да се отървете от знака модул във всички неравенства.
Пример 8 Решете неравенството
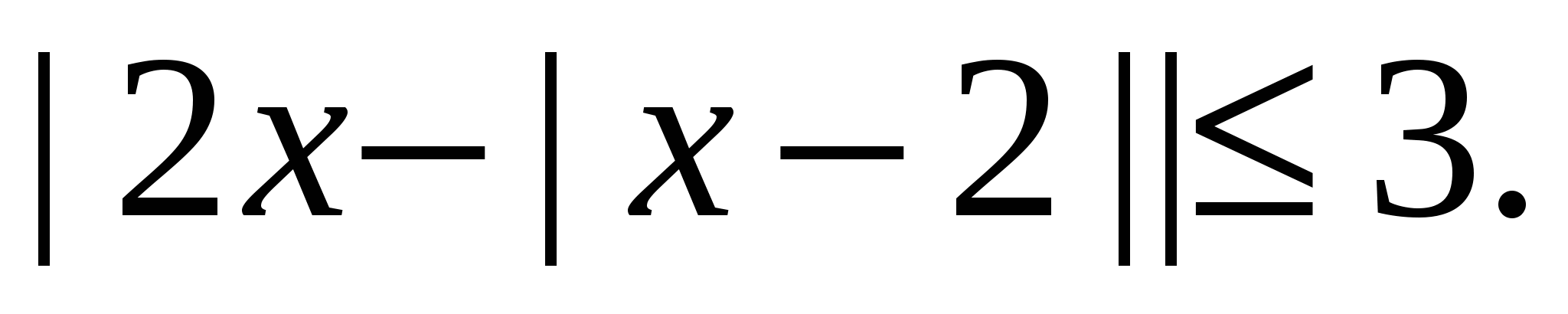
Решение.



Отговор.  .
.
3. Графично решаване на уравнения и неравенства с модул
Решаването на уравнения, съдържащи знака на абсолютната стойност, често е много по-удобно за решаване не аналитично, а графично (особено уравнения, съдържащи параметри).
Пример 9(C5, ИЗПОЛЗВАНЕ - 2010)
° С5. За всяка стойноста
посочете броя на решенията на уравнението 
Решение.Нека начертаем функцията
 . За да направите това, изберете цял квадрат:
. За да направите това, изберете цял квадрат:
Броят на точките на пресичане на графиката на функцията y \u003d  с хоризонтални линии y = a е равно на броя на решенията на уравнението.
с хоризонтални линии y = a е равно на броя на решенията на уравнението.
О  отговор:
ако
отговор:
ако  < 0, то решений нет; если а= 0, то два решения, если
< 0, то решений нет; если а= 0, то два решения, если  0 < а < 4, то четыре решения; если а=4, то три решения; если а >4, след това две решения.
0 < а < 4, то четыре решения; если а=4, то три решения; если а >4, след това две решения.
Други начини за решаване на уравнения и неравенства с модула
Метод на разширяване на модула
Нека да разгледаме метода за разширяване на модула, използвайки пример:
Пример 10 реши уравнението
Решение.Това уравнение съдържа повече от един модул.
Методът за решаване на уравнения, съдържащи променливи под знака на два или повече модула, е както следва.
1. Намерете стойностите на променливата, за която всеки от модулите изчезва: 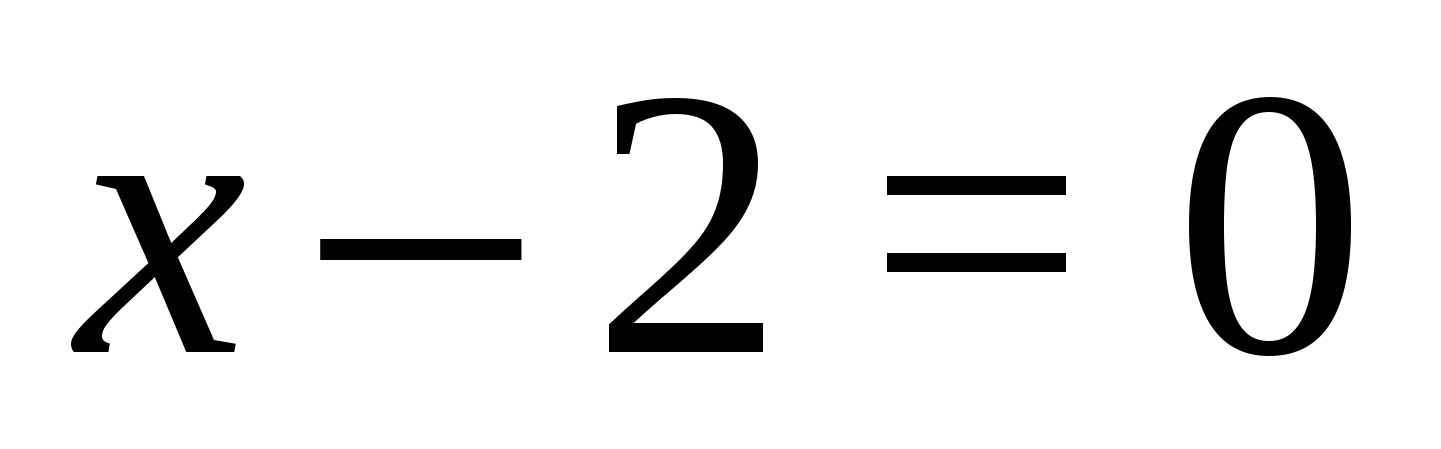 ,
,  ;
;  ,
,  ;
;  ,
,  .
.
2. Маркирайте тези точки на числовата ос.
3. Разглеждаме уравнението на всеки от интервалите и задаваме знака на изразите, които са под модулите.
1) Кога  или
или  . За да определите знака на всеки от изразите под модула на този интервал, достатъчно е да вземете произволна стойност
. За да определите знака на всеки от изразите под модула на този интервал, достатъчно е да вземете произволна стойност  от този интервал и заместете в израза. Ако получената стойност е отрицателна, тогава за всички
от този интервал и заместете в израза. Ако получената стойност е отрицателна, тогава за всички  от този интервал изразът ще бъде отрицателен; ако получената числена стойност е положителна, тогава за всички стойности
от този интервал изразът ще бъде отрицателен; ако получената числена стойност е положителна, тогава за всички стойности  от този интервал изразът ще бъде положителен.
от този интервал изразът ще бъде положителен.
Да вземем стойността  от празнината
от празнината  и заместете стойността му в израза
и заместете стойността му в израза 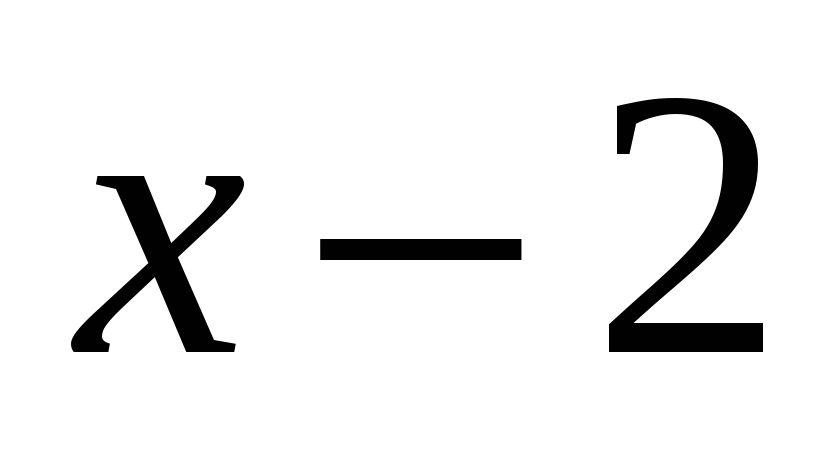 , получаваме
, получаваме  , така че на този интервал
, така че на този интервал 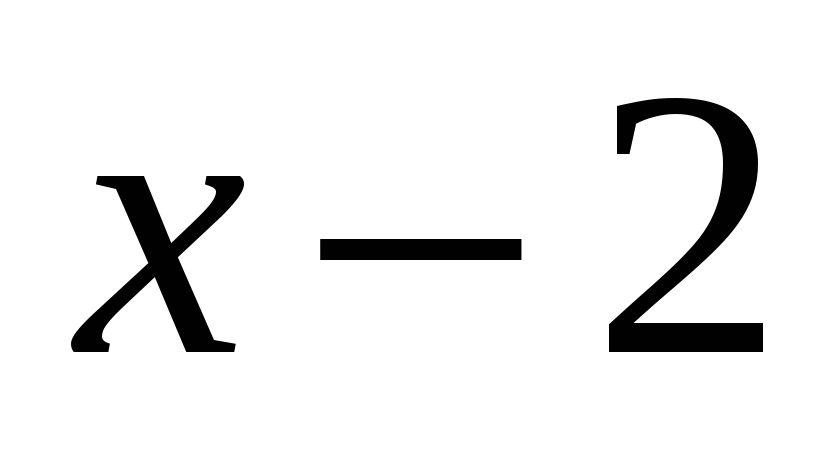 е отрицателна и следователно ``вън" от под модула със знак ``минус"", получаваме:
е отрицателна и следователно ``вън" от под модула със знак ``минус"", получаваме: 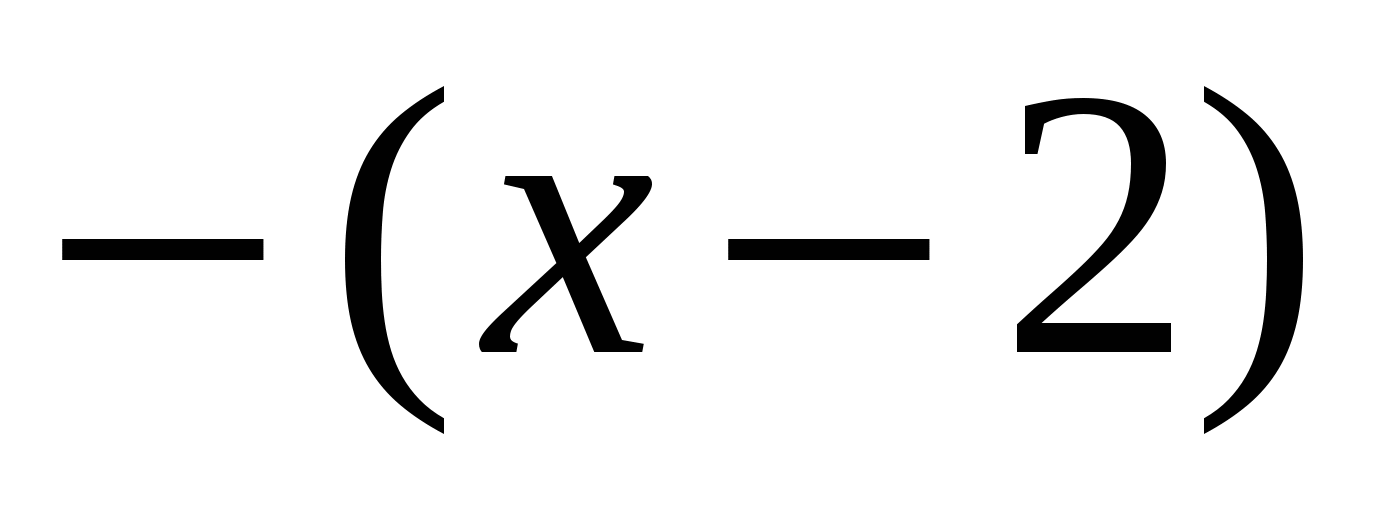 .
.
С тази стойност  , израз
, израз  ще получи стойността
ще получи стойността 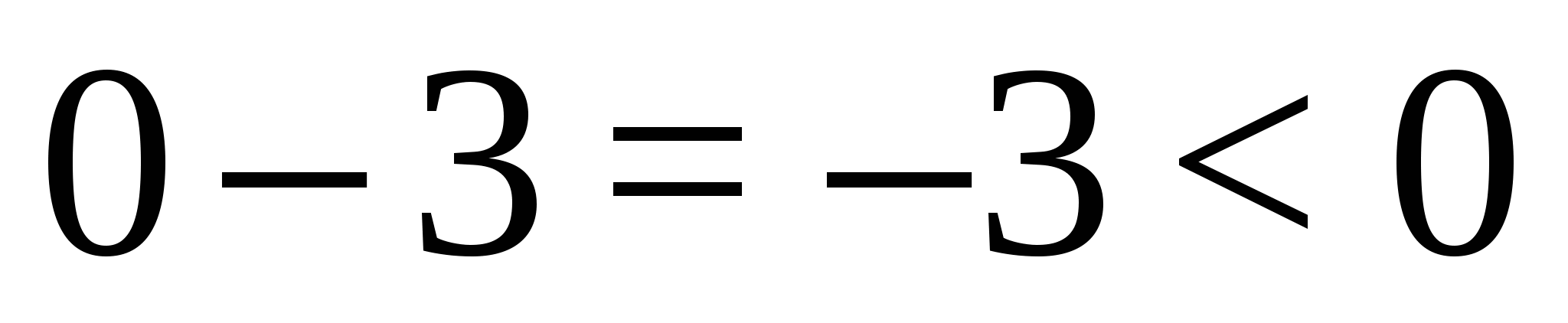 , така че е в интервала
, така че е в интервала  също приема отрицателни стойности и ``напуска"" от модула със знак ``минус``, получаваме:
също приема отрицателни стойности и ``напуска"" от модула със знак ``минус``, получаваме:  .
.
Изразяване 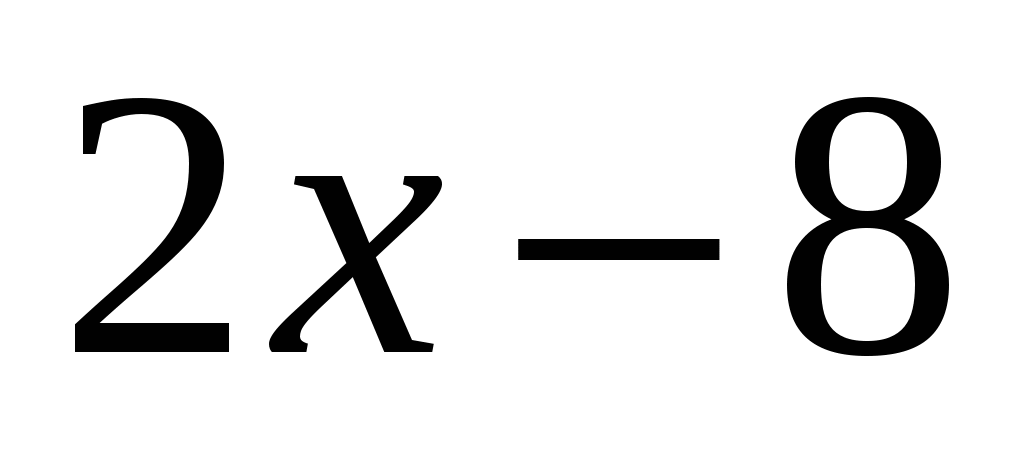 ще получи стойността
ще получи стойността  и "излиза" от модула със знак "минус":
и "излиза" от модула със знак "минус":  .
.
Уравнението на този интервал ще се окаже, както следва: , решавайки го, намираме:  .
.
Разберете дали тази стойност е в диапазона  . Оказва се, че е включено
. Оказва се, че е включено  е коренът на уравнението.
е коренът на уравнението.
2) Кога  . Изберете произволна стойност
. Изберете произволна стойност  от този интервал. Позволявам
от този интервал. Позволявам 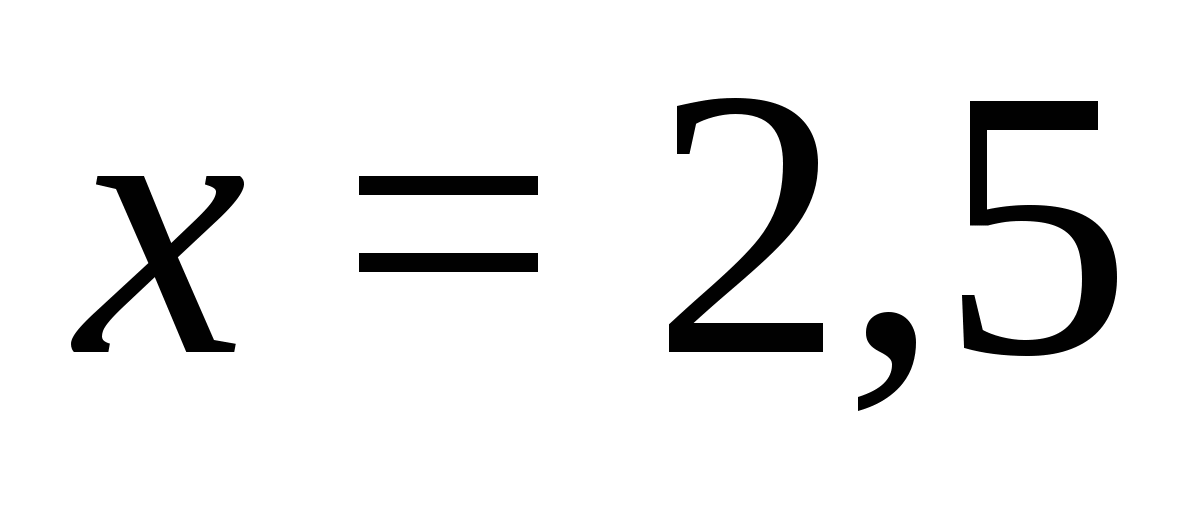 . Определяме знака на всеки от изразите под модула при тази стойност
. Определяме знака на всеки от изразите под модула при тази стойност  . Оказва се, че изразът
. Оказва се, че изразът 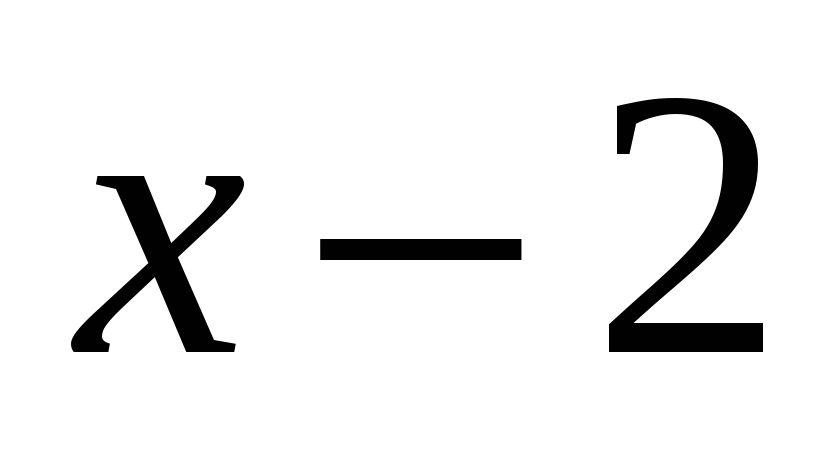 положителни, а другите две са отрицателни.
положителни, а другите две са отрицателни.
Уравнението на този интервал ще приеме формата: . Решавайки го, намираме  . Тази стойност не е включена в диапазона
. Тази стойност не е включена в диапазона 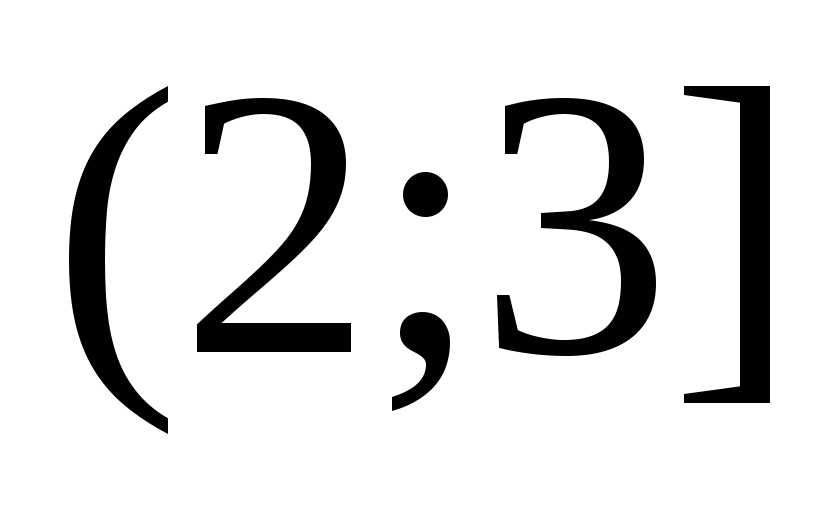 , което означава, че не е корен на уравнението.
, което означава, че не е корен на уравнението.
3) Кога 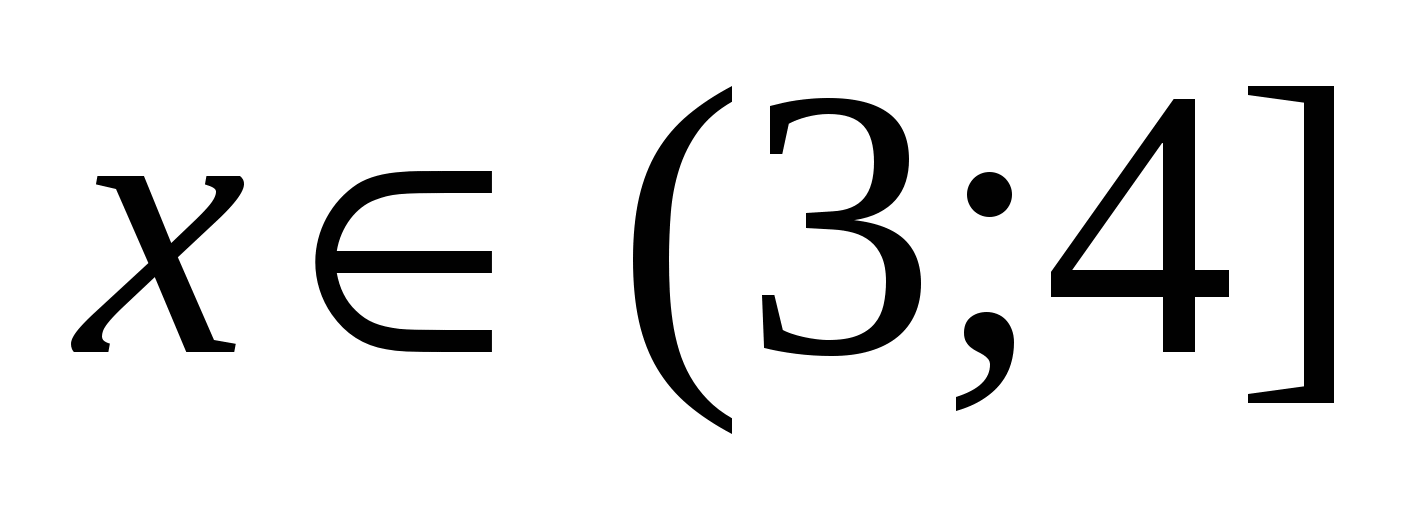 . Изберете произволна стойност
. Изберете произволна стойност  от този интервал, да речем,
от този интервал, да речем,  и заменете във всеки от изразите. Откриваме, че изразите
и заменете във всеки от изразите. Откриваме, че изразите 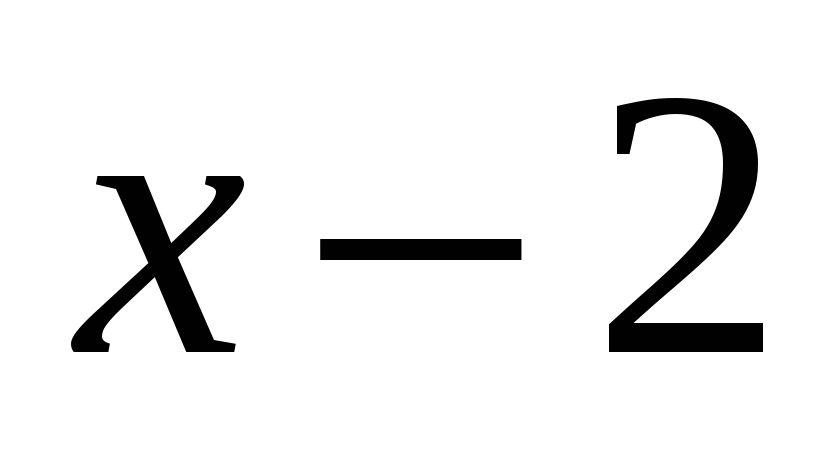 и
и  са положителни и
са положителни и 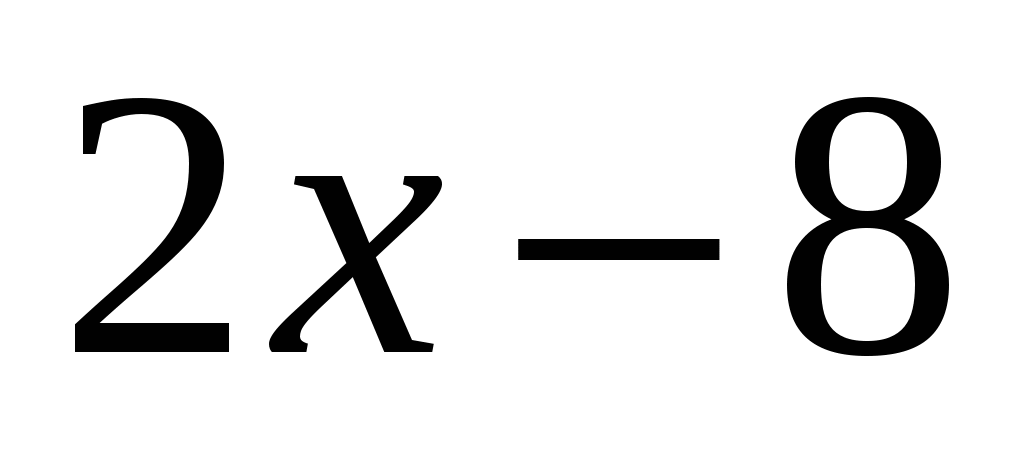 - отрицателно. Получаваме следното уравнение: .
- отрицателно. Получаваме следното уравнение: .
След трансформацията получаваме:  , което означава, че уравнението няма корени в този интервал.
, което означава, че уравнението няма корени в този интервал.
4) Кога  . Лесно е да се установи, че всички изрази на този интервал са положителни, което означава, че получаваме уравнението:
. Лесно е да се установи, че всички изрази на този интервал са положителни, което означава, че получаваме уравнението: 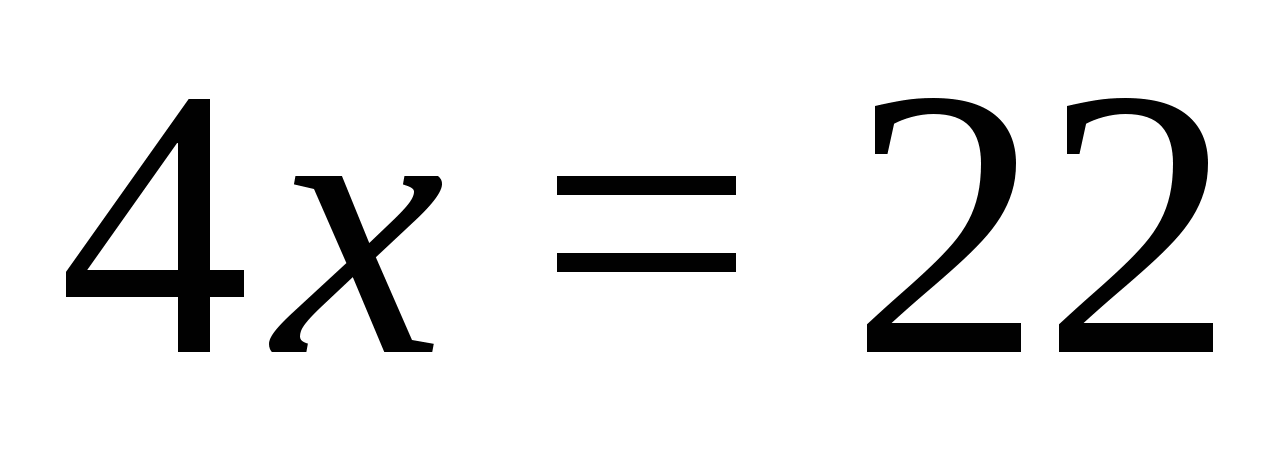 ,
,  който е включен в интервала и е коренът на уравнението.
който е включен в интервала и е коренът на уравнението.
Отговор.  ,
,  .
.
Решение на уравнения, съдържащи модули на неотрицателни изрази
Пример 11 Каква е сумата от корените на уравнението (коренът, ако е един) на уравнението

Решение.Помислете за израза
 и го трансформирайте във формата
и го трансформирайте във формата 
Очевидно е, че числителят на дроб за всякакви стойности на променливата е положително число. Така че дробният израз е положителен ако  (защото
(защото  ). Трансформираме получения израз, предоставен
). Трансформираме получения израз, предоставен  . Получаваме уравнение, еквивалентно на оригиналното:
. Получаваме уравнение, еквивалентно на оригиналното:

Отговор.  .
.
Пример 12 реши уравнението

Решение.Тъй като лявата страна на уравнението е неотрицателна, за всички допустими стойности на променливата, върху множеството от корени на уравнението, дясната му страна също трябва да е неотрицателна, следователно условието  , на този интервал знаменателите на двете дроби са равни и остава да се реши уравнението
, на този интервал знаменателите на двете дроби са равни и остава да се реши уравнението  . Решаване и отчитане на ограничението
. Решаване и отчитане на ограничението  , получаваме
, получаваме
Отговор.  .
.
Решаване на уравнения с помощта на геометрична интерпретация
Геометричният смисъл на израза 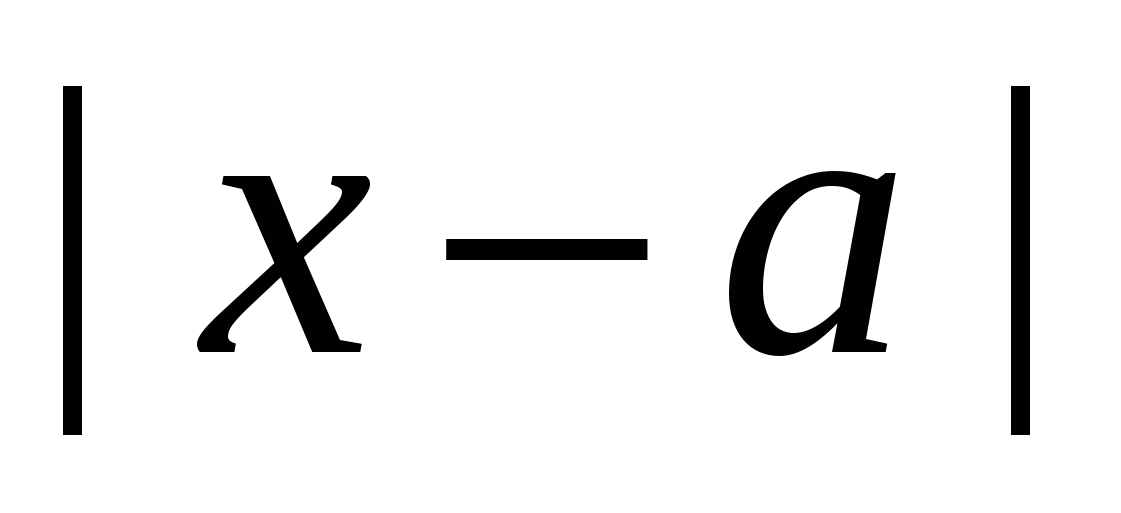 - дължината на сегмента от координатната ос, свързващ точките с абсцисите
- дължината на сегмента от координатната ос, свързващ точките с абсцисите  и
и  . Преводът на алгебричен проблем на геометричен език често прави възможно избягването на тромави изчисления.
. Преводът на алгебричен проблем на геометричен език често прави възможно избягването на тромави изчисления.
Пример 13 Нека решим уравнението  .
.
Решение.Ще аргументираме следното: въз основа на геометричната интерпретация на модула, лявата страна на уравнението е сумата от разстоянията от някаква точка с абсцисата  до две фиксирани точки с абсцисите 1 и 2. След това всички точки с абсцисите от отсечката
до две фиксирани точки с абсцисите 1 и 2. След това всички точки с абсцисите от отсечката  притежават изискваното свойство, докато точките, разположени извън този сегмент, нямат.
притежават изискваното свойство, докато точките, разположени извън този сегмент, нямат.
Отговор.  .
.
Пример 14 Решете неравенството  .
.
Решение.Начертайте точки на координатната линия, сумата от разстоянията от които до точките  и
и  е точно равно на
е точно равно на  . Всичко това са гранични точки
. Всичко това са гранични точки 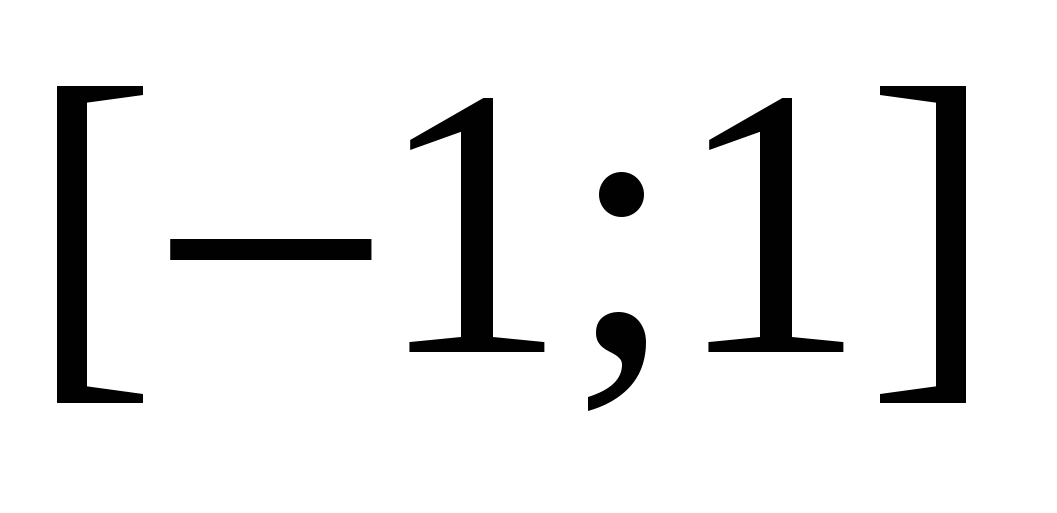 . За всички числа извън този сегмент сумата от разстоянията ще бъде по-голяма от две.
. За всички числа извън този сегмент сумата от разстоянията ще бъде по-голяма от две.
Отговор. 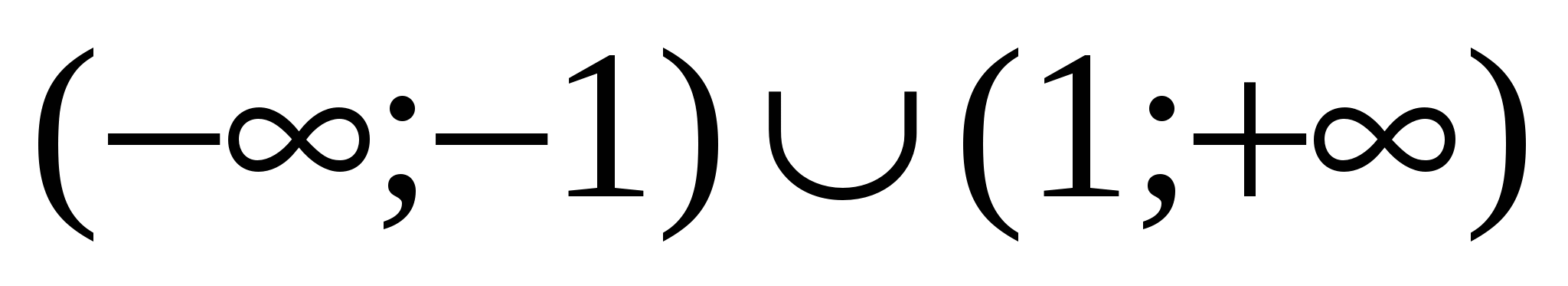 .
.
Пример(C3, ИЗПОЛЗВАНЕ - 2010) 15 реши уравнението

Решение.Прилагане на идентичността два пъти 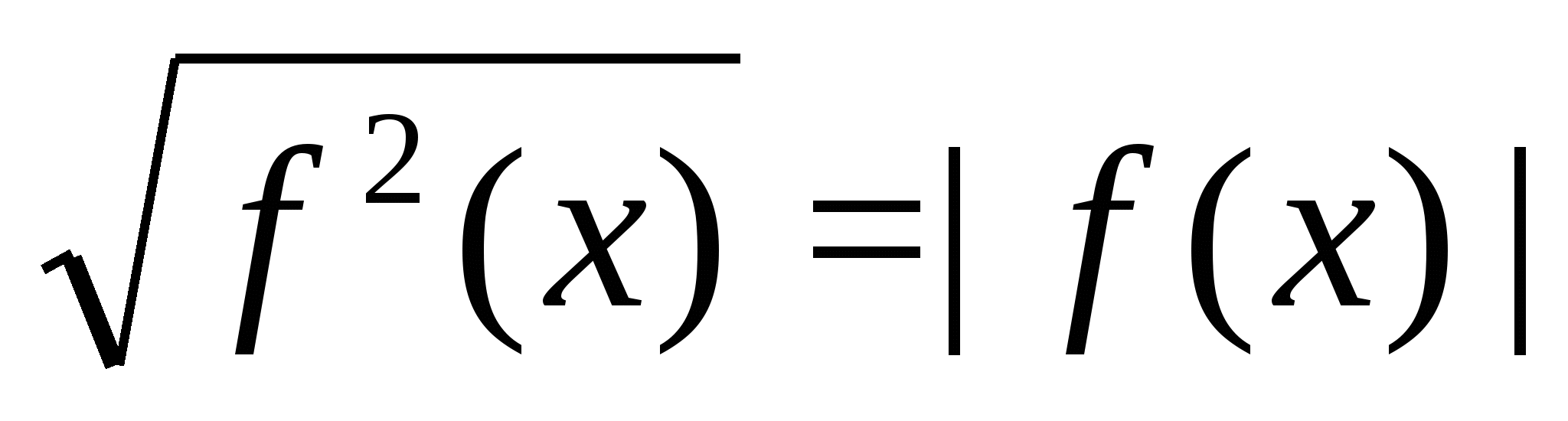 , получаваме уравнението
, получаваме уравнението

чието решение е интервалът  .
.
Отговор.  .
.
Пример(C3, ИЗПОЛЗВАНЕ - 2011) 16 17 реши уравнението
Решение. .
Отговор.  .
.
Прилагане на теоремата за знака при решаване на уравнения
Ние формулираме теорема, удобна за решаване на неравенства относно продукти или частични разлики на модули:
Теорема 18 Знакът на разликата между модулите на два израза съвпада със знака на разликата на квадратите на тези изрази.
не изчезва за никоя стойност на променливата. Това означава, че функцията е с постоянен знак в цялата област на дефиниция. Чрез изчисляване напр.  , получаваме, че функцията приема само положителни стойности.
, получаваме, че функцията приема само положителни стойности.
Отговор.  .
.
Интервалният метод ви позволява да решавате по-сложни уравнения и неравенства с модули, но в този случай той има малко по-различна цел. Въпросът е следният. Ние намираме корените на всички подмодулни изрази и разделяме числената ос на интервали на постоянство на знака на тези изрази. Това позволява, преминавайки последователно през тези интервали, едновременно да се отървете от всички модули и да решите обичайното уравнение или неравенство (докато проверявате дали намереният отговор е включен в дадения интервал).
Решаване на уравнения чрез умножение с положителен множител
Заключение.
Обобщавайки нашата работа, можем да кажем следното.
Целта на работата беше да се проучат различни методи за решаване на уравнения и неравенства с модули.
Разглеждат се някои разновидности на най-простите уравнения и неравенства с модул, които могат да бъдат решени с помощта на еквивалентни преходи, както и теореми за сбора на модулите; графичен начин за решаване на уравнения. Трябва да се каже, че в училищния курс по математика най-често се използват тези методи за решаване. Графичният метод е особено актуален при решаване на задачи° С 5 от контролно-измервателните материали на изпита.
След това проучихме, използвайки няколко примера, други методи за решаване на уравнения и неравенства с модули, а именно: методът на разширяване на модулите; решение на уравнения, съдържащи модули от неотрицателни изрази; решаване на уравнения чрез геометрична интерпретация; използване на самоличността 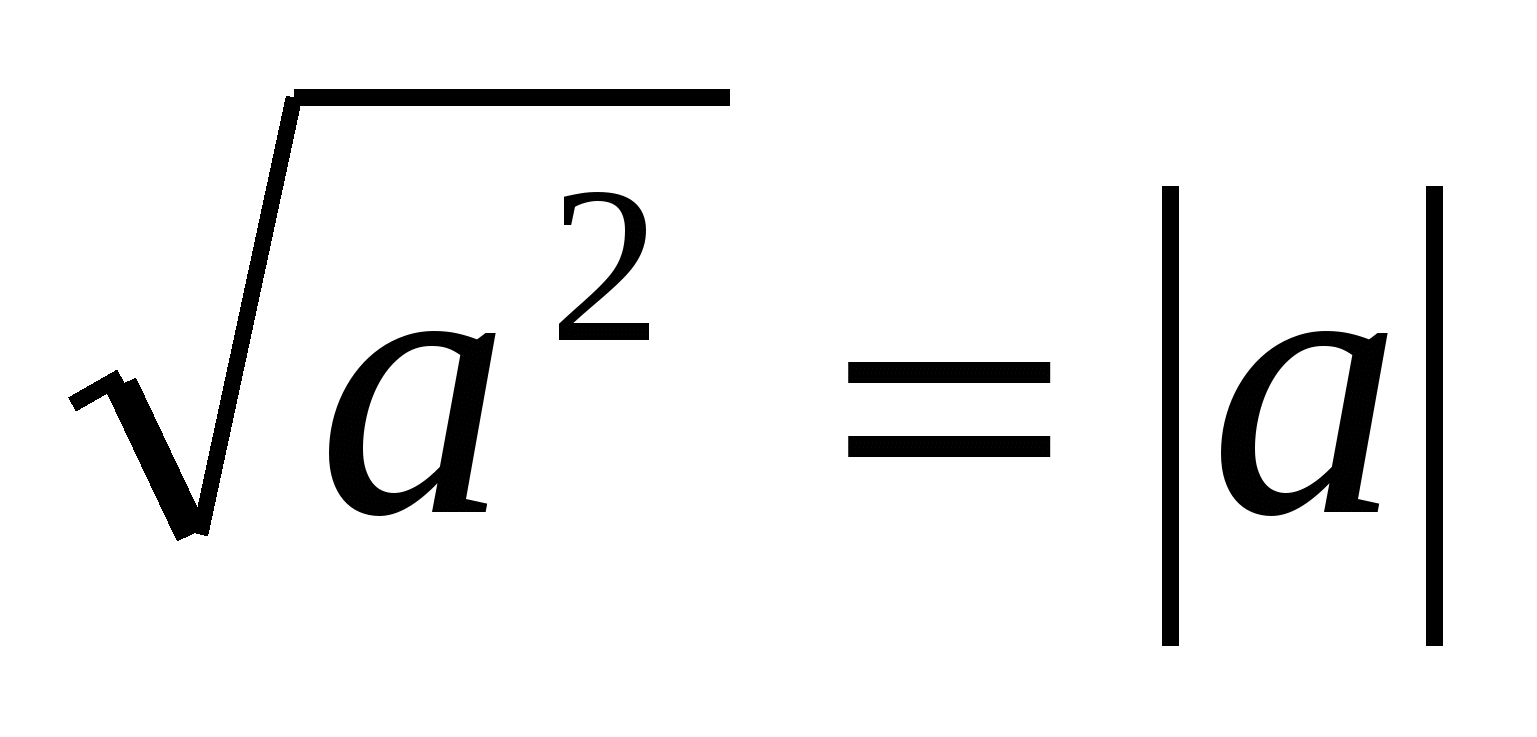 ; приложение на теоремата за знака; решаване на уравнения чрез преминаване към следствие, умножение с положителен множител, както и решаване на неравенства по метода на интервалите.
; приложение на теоремата за знака; решаване на уравнения чрез преминаване към следствие, умножение с положителен множител, както и решаване на неравенства по метода на интервалите.
Така в хода на изследването стигнахме до следните изводи.
За най-универсални и приложими за най-голям брой задачи смятаме метода на модулно разширение, графичния метод и интервалния метод. Това убеждение възникна в резултат на решаването на голям брой задачи от тестовите материали на Единния държавен изпит, предметни първенства, олимпиадни задачи, както и изучаване на литературата по този въпрос. Също така считаме за много важно да познаваме и прилагаме идентичността 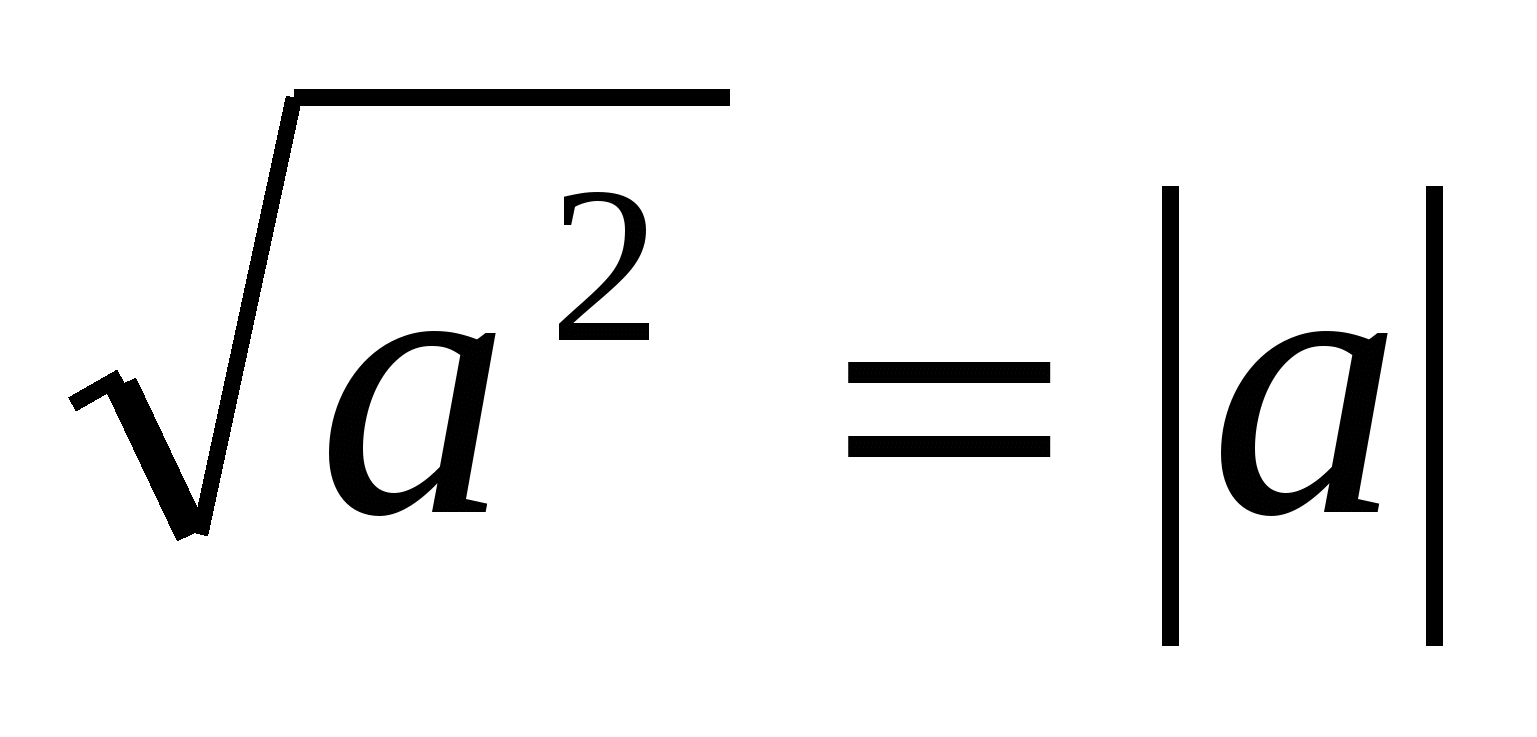 , тъй като се използва не само за решаване на уравнения и неравенства, но и за трансформиране на много изрази с радикали. Останалите методи за решаване, които разгледахме, разбира се, са от голям интерес по отношение на разширяването на математическите хоризонти и общото математическо развитие. Затова планираме да ги използваме за подготовка за държавна окончателна атестация под формата на Единен държавен изпит и подготовка за обучение във висше учебно заведение.
, тъй като се използва не само за решаване на уравнения и неравенства, но и за трансформиране на много изрази с радикали. Останалите методи за решаване, които разгледахме, разбира се, са от голям интерес по отношение на разширяването на математическите хоризонти и общото математическо развитие. Затова планираме да ги използваме за подготовка за държавна окончателна атестация под формата на Единен държавен изпит и подготовка за обучение във висше учебно заведение.
Библиография.
"Голяма математическа енциклопедия" за ученици и студенти;
Математика. USE - 2011, 2012. Стандартни опции за изпит. / Под редакцията на A.L. Семенова, И.В. Ященко.
М.Я. Вигодски. Наръчник по елементарна математика
„Най-новият ученически справочник”;
Енциклопедия „Аз познавам света. Математика";
;
модулно числосамото това число се нарича, ако е неотрицателно, или същото число с обратен знак, ако е отрицателно.
Например модулът на 6 е 6, а модулът на -6 също е 6.
Тоест, модулът на числото се разбира като абсолютна стойност, абсолютната стойност на това число, без да се взема предвид неговият знак.
Означава се както следва: |6|, | х|, |а| и т.н.
(За повече подробности вижте раздела „Модул на числото“).
Модулни уравнения.
Пример 1 . реши уравнението|10 х - 5| = 15.
Решение.
В съответствие с правилото уравнението е еквивалентно на комбинация от две уравнения:
10х - 5 = 15
10х - 5 = -15
Ние решаваме:
10х = 15 + 5 = 20
10х = -15 + 5 = -10
х = 20: 10
х = -10: 10
х = 2
х = -1
Отговор: х 1 = 2, х 2 = -1.
Пример 2 . реши уравнението|2 х + 1| = х + 2.
Решение.
Тъй като модулът е неотрицателно число, тогава х+ 2 ≥ 0. Съответно:
х ≥ -2.
Правим две уравнения:
2х + 1 = х + 2
2х + 1 = -(х + 2)
Ние решаваме:
2х + 1 = х + 2
2х + 1 = -х - 2
2х - х = 2 - 1
2х + х = -2 - 1
х = 1
х = -1
И двете числа са по-големи от -2. И двете са корени на уравнението.
Отговор: х 1 = -1, х 2 = 1.
Пример 3
. реши уравнението
|х + 3| - 1
————— = 4
х - 1
Решение.
Уравнението има смисъл, ако знаменателят не е равен на нула - така че ако х≠ 1. Нека вземем предвид това условие. Първото ни действие е просто - ние не просто се отърваваме от фракцията, но я трансформираме по такъв начин, че да получим модула в най-чистата му форма:
|х+ 3| - 1 = 4 ( х - 1),
|х + 3| - 1 = 4х - 4,
|х + 3| = 4х - 4 + 1,
|х + 3| = 4х - 3.
Сега имаме само израза под модула от лявата страна на уравнението. Продължа напред.
Модулът на числото е неотрицателно число - тоест трябва да е по-голямо или равно на нула. Съответно решаваме неравенството:
4х - 3 ≥ 0
4х ≥ 3
х ≥ 3/4
Така имаме второ условие: коренът на уравнението трябва да бъде поне 3/4.
В съответствие с правилото съставяме набор от две уравнения и ги решаваме:
х + 3 = 4х - 3
х + 3 = -(4х - 3)
х + 3 = 4х - 3
х + 3 = -4х + 3
х - 4х = -3 - 3
х + 4х = 3 - 3
х = 2
х = 0
Получихме два отговора. Нека проверим дали те са корените на първоначалното уравнение.
Имахме две условия: коренът на уравнението не може да бъде равен на 1 и трябва да бъде поне 3/4. Това е х ≠ 1, х≥ 3/4. И двете условия отговарят само на един от двата получени отговора - числото 2. Следователно само то е коренът на първоначалното уравнение.
Отговор: х = 2.
Неравенства с модула.
Пример 1 . Решете неравенството| х - 3| < 4
Решение.
Правилото на модула казва:
|а| = а, ако а ≥ 0.
|а| = -а, ако а < 0.
Модулът може да има както неотрицателно, така и отрицателно число. Така че трябва да разгледаме и двата случая: х- 3 ≥ 0 и х - 3 < 0.
1) Кога х- 3 ≥ 0 нашето първоначално неравенство остава както е, само без знака модул:
х - 3 < 4.
2) Кога х - 3 < 0 в исходном неравенстве надо поставить знак минус перед всем подмодульным выражением:
-(х - 3) < 4.
Отваряйки скобите, получаваме:
-х + 3 < 4.
Така от тези две условия стигнахме до обединението на две системи от неравенства:
х - 3 ≥ 0
х - 3 < 4
х - 3 < 0
-х + 3 < 4
Нека ги решим:
х ≥ 3
х < 7
х < 3
х > -1
И така, в нашия отговор имаме обединението на две множества:
3 ≤ х < 7 U -1 < х < 3.
Определете най-малката и най-голямата стойност. Това са -1 и 7. В същото време хпо-голямо от -1, но по-малко от 7.
Освен това, х≥ 3. Следователно решението на неравенството е целият набор от числа от -1 до 7, с изключение на тези крайни числа.
Отговор: -1 < х < 7.
Или: х ∈ (-1; 7).
Добавки.
1) Има по-прост и кратък начин за решаване на нашето неравенство - графично. За да направите това, начертайте хоризонтална ос (фиг. 1).
Израз | х - 3| < 4 означает, что расстояние от точки хкъм точка 3 по-малко от четири единици. Отбелязваме цифрата 3 на оста и броим 4 деления отляво и отдясно на нея. Отляво ще стигнем до точка -1, отдясно - до точка 7. Така точките хпросто видяхме, без да ги изчисляваме.
Освен това, според условието за неравенство, самите -1 и 7 не са включени в набора от решения. Така получаваме отговора:
1 < х < 7.
2) Но има друго решение, което е дори по-просто от графичния начин. За да направим това, нашето неравенство трябва да бъде представено в следната форма:
4 < х - 3 < 4.
Все пак така е по правилото на модула. Неотрицателното число 4 и подобно отрицателно число -4 са границите на решението на неравенството.
4 + 3 < х < 4 + 3
1 < х < 7.
Пример 2 . Решете неравенството| х - 2| ≥ 5
Решение.
Този пример се различава значително от предишния. Лявата страна е по-голяма от 5 или равна на 5. От геометрична гледна точка решението на неравенството са всички числа, които са на разстояние 5 единици или повече от точка 2 (фиг. 2). Графиката показва, че това са всички числа, които са по-малки или равни на -3 и по-големи или равни на 7. И така, вече сме получили отговора.
Отговор: -3 ≥ х ≥ 7.
По пътя решаваме същото неравенство, като пренареждаме свободния член наляво и надясно с противоположния знак:
5 ≥ х - 2 ≥ 5
5 + 2 ≥ х ≥ 5 + 2
Отговорът е същият: -3 ≥ х ≥ 7.
Или: х ∈ [-3; 7]
Примерът е решен.
Пример 3 . Решете неравенството 6 х 2 - | х| - 2 ≤ 0
Решение.
Номер хможе да бъде положителен, отрицателен или нула. Следователно трябва да вземем предвид и трите обстоятелства. Както знаете, те се вземат предвид в две неравенства: х≥ 0 и х < 0. При х≥ 0, ние просто пренаписваме нашето оригинално неравенство, както е, само без знака модул:
6x 2 - х - 2 ≤ 0.
Сега за втория случай: ако х < 0. Модулем отрицателно числое същото число с противоположен знак. Тоест, записваме числото под модула с противоположния знак и отново се отърваваме от знака за модул:
6х 2 - (-х) - 2 ≤ 0.
Разширяване на скобите:
6х 2 + х - 2 ≤ 0.
Така получихме две системи от уравнения:
6х 2 - х - 2 ≤ 0
х ≥ 0
6х 2 + х - 2 ≤ 0
х < 0
Трябва да решим неравенства в системи - което означава, че трябва да намерим корените на две квадратни уравнения. За да направим това, приравняваме левите части на неравенствата към нула.
Да започнем с първия:
6х 2 - х - 2 = 0.
Как се решава квадратно уравнение - вижте раздела "Квадрично уравнение". Веднага ще назовем отговора:
х 1 \u003d -1/2, x 2 \u003d 2/3.
От първата система от неравенства получаваме, че решението на първоначалното неравенство е целият набор от числа от -1/2 до 2/3. Ние пишем съюза на решенията за х ≥ 0:
[-1/2; 2/3].
Сега нека решим второто квадратно уравнение:
6х 2 + х - 2 = 0.
Корените му:
х 1 = -2/3, х 2 = 1/2.
Заключение: кога х < 0 корнями исходного неравенства являются также все числа от -2/3 до 1/2.
Нека комбинираме двата отговора и да получим крайния отговор: решението е целият набор от числа от -2/3 до 2/3, включително тези екстремни числа.
Отговор: -2/3 ≤ х ≤ 2/3.
Или: х ∈ [-2/3; 2/3].
Тази статия е посветена на техники за решаване на различни уравнения и неравенства, съдържащи
променлива под знака на модула.
Ако на изпита срещнете уравнение или неравенство с модул, можете да го решите,
без да познава никакви специални методи и използва само дефиницията на модула. Истина,
може да отнеме час и половина ценно време за изпит.
Затова искаме да ви разкажем за техники, които опростяват решаването на такива проблеми.
Преди всичко нека си припомним това
![]()
Помислете за различни видове уравнения с модул. (Повече за неравенствата по-късно.)
Ляв модул, десен номер
Това е най-простият случай. Нека решим уравнението
Има само две числа, чийто модул е четири. Това са 4 и -4. Следователно уравнението
е еквивалентен на комбинация от две прости:
Второто уравнение няма решения. Решения на първото: x = 0 и x = 5.
Отговор: 0; 5.
Променлива както под модула, така и извън модула
Тук трябва да разширите модула по дефиниция. . . или си представете!
Уравнението се разделя на два случая в зависимост от знака на израза под модула.
С други думи, това е еквивалентно на комбинацията от две системи:
![]()
Решение на първата система: . Втората система няма решения.
Отговор: 1.
Първи случай: x ≥ 3. Премахнете модула:
Числото , тъй като е отрицателно, не отговаря на условието x ≥ 3 и следователно не е корен на първоначалното уравнение.
Нека разберем дали числото отговаря на това условие. За да направим това, правим разликата и определяме нейния знак:
Следователно, повече от три и следователно е коренът на първоначалното уравнение
Втори случай: x< 3. Снимаем модуль:
номер . е по-голямо от и следователно не отговаря на условието x< 3. Проверим :
Означава,. е коренът на първоначалното уравнение.
Премахване на модула по дефиниция? Страшно е дори да си помислим за това, защото дискриминантът не е перфектен квадрат. Нека използваме по-добре следното съображение: уравнение от формата |A| = B е еквивалентно на комбинация от две системи:
![]()
Същото, но малко по-различно:
С други думи, решаваме две уравнения, A = B и A = −B, и след това избираме корените, които отговарят на условието B ≥ 0.
Да започваме. Първо решаваме първото уравнение:
След това решаваме второто уравнение:
Сега във всеки случай проверяваме знака на дясната страна:
Следователно, само и са подходящи.
Квадратни уравнения с |x| = t
Нека решим уравнението:
Тъй като , е удобно да направите промяната |x| = t. Получаваме:
![]()
Отговор: ±1.
Модул е равен на модул
Говорим за уравнения от вида |A| = |B|. Това е подарък от съдбата. Без модулни разширения по дефиниция! Просто е:
Например, разгледайте уравнението: . Той е еквивалентен на следния набор:
Остава да се реши всяко от уравненията на населението и да се запише отговорът.
Два или повече модула
Нека решим уравнението:
Няма да се занимаваме с всеки модул поотделно и да го отваряме по дефиниция - ще има твърде много опции. Има по-рационален начин - методът на интервалите.
Изразите под модулите се нулират в точките x = 1, x = 2 и x = 3. Тези точки разделят числовата права на четири интервала (интервали). Отбелязваме тези точки на числовата ос и поставяме знаците за всеки от изразите под модулите върху получените интервали. (Редът на знаците е същият като реда на съответните модули в уравнението.)

Така трябва да разгледаме четири случая – когато х е във всеки от интервалите.
Случай 1: x ≥ 3. Всички модули се премахват "с плюс":
Получената стойност x = 5 удовлетворява условието x ≥ 3 и следователно е коренът на първоначалното уравнение.
Случай 2: 2 ≤ x ≤ 3. Последният модул вече е премахнат "с минус":
Получената стойност на x също е подходяща - принадлежи към разглеждания интервал.
Случай 3: 1 ≤ x ≤ 2. Вторият и третият модул се премахват "с минус":
Получихме правилното числено равенство за всяко x от разглеждания интервал, те служат като решения на това уравнение.
Случай 4: x ≤ 1 ≤ 1. Вторият и третият модул се премахват "с минус":
Нищо ново. Вече знаем, че x = 1 е решение.
Отговор: ∪ (5).
Модул в модула
Нека решим уравнението:
Започваме с разширяване на вътрешния модул.
1) x ≤ 3. Получаваме:
Изразът под модула изчезва при . Тази точкапринадлежи към разглежданите
интервал. Следователно трябва да разгледаме два подслучая.
1.1) В този случай получаваме:
Тази стойност на x не е добра, защото не принадлежи към разглеждания интервал.
1.2). Тогава:
Тази стойност x също не е добра.
Така че за x ≤ 3 няма решения. Да преминем към втория случай.
2) x ≥ 3. Имаме:
Тук имаме късмет: изразът x + 2 е положителен в разглеждания интервал! Следователно вече няма да има подслучаи: модулът се премахва „с плюс“:
Тази стойност на x е в разглеждания интервал и следователно е коренът на първоначалното уравнение.
Така се решават всички задачи от този тип - отваряме последователно вложените модули, започвайки от вътрешния.
Математика е символ на мъдростта на науката,
пример за научна строгост и простота,
стандартът за съвършенство и красота в науката.
Руски философ, професор А.В. Волошинов
Модулни неравенства
Най-трудните за решаване задачи по математика в училище са неравенствата, съдържащи променливи под знака на модула. За успешното решаване на такива неравенства е необходимо да познавате добре свойствата на модула и да имате уменията да ги използвате.
Основни понятия и свойства
Модул (абсолютна стойност) на реално числообозначен и се определя, както следва:
Простите свойства на модула включват следните отношения:
И .
Забележка, че последните две свойства са валидни за всяка четна степен.
Освен това, ако , където , тогава и
По-сложни свойства на модула, които могат ефективно да се използват при решаване на уравнения и неравенства с модули, се формулират с помощта на следните теореми:
Теорема 1.За всякакви аналитични функциии неравенството.
Теорема 2.Равенство е еквивалентно на неравенството.
Теорема 3.Равенство е еквивалентно на неравенството.
Най-често срещаните неравенства в училищната математика, съдържащи неизвестни променливи под знака модул, са неравенства от видаи къде някаква положителна константа.
Теорема 4.Неравенство е еквивалентно на двойно неравенство, и решението на неравенствотосе свежда до решаване на набор от неравенстваи .
Тази теорема е частен случай на теореми 6 и 7.
По-сложни неравенства, съдържащи модула са неравенства от вида, и .
Методите за решаване на такива неравенства могат да бъдат формулирани с помощта на следните три теореми.
Теорема 5.Неравенство е еквивалентна на комбинацията от две системи от неравенства
И (1)
Доказателство.От тогава
Това предполага валидността на (1).
Теорема 6.Неравенство е еквивалентна на системата от неравенства
Доказателство.защото, след това от неравенствотоследва това . При това условие неравенствотои в този случай втората система от неравенства (1) се оказва несъстоятелна.
Теоремата е доказана.
Теорема 7.Неравенство е еквивалентно на комбинация от едно неравенство и две системи от неравенства
И (3)
Доказателство.Тъй като , Тогава неравенството винаги се изпълнява, ако .
Позволявам , тогава неравенствотоще бъде равносилно на неравенство, от което следва множеството от две неравенстваи .
Теоремата е доказана.
Помислете за типични примери за решаване на проблеми по темата „Неравенства, съдържащи променливи под знака на модула.
Решаване на неравенства с модул
Повечето прост методрешаването на неравенства с модул е методът, въз основа на разширяване на модула. Този метод е общ, но в общия случай приложението му може да доведе до много тромави изчисления. Следователно учениците трябва да знаят и други (по-ефективни) методи и техники за решаване на такива неравенства. По-специално, трябва да притежавате умения за прилагане на теореми, дадени в тази статия.
Пример 1Решете неравенството
. (4)
Решение.Неравенство (4) ще се решава по "класическия" метод - метода на разлагане на модулите. За тази цел прекъсваме числовата осточки и интервали и разгледайте три случая.
1. Ако , то , , , и неравенството (4) приема форматаили .
Тъй като случаят се разглежда тук, , е решение на неравенство (4).
2. Ако , то от неравенство (4) получавамеили . Тъй като пресичането на интервалии празно е, то на разглеждания интервал няма решения на неравенство (4).
3. Ако , тогава неравенството (4) приема форматаили . Очевидно е, че също е решение на неравенство (4).
Отговор: , .
Пример 2Решете неравенството.
Решение.Да приемем, че. защото, тогава даденото неравенство приема форматаили . От тогава и оттук следваили .
Въпреки това, следователно или.
Пример 3Решете неравенството
. (5)
Решение.защото, тогава неравенство (5) е еквивалентно на неравенстватаили . Оттук, съгласно теорема 4, имаме набор от неравенстваи .
Отговор: , .
Пример 4Решете неравенството
. (6)
Решение.Нека обозначим . Тогава от неравенство (6) получаваме неравенствата , , или .
Оттук, използвайки интервалния метод, получаваме . защото, тогава тук имаме система от неравенства
Решението на първото неравенство от системата (7) е обединението на два интервалаи , а решението на второто неравенство е двойното неравенство. Това предполага , че решението на системата от неравенства (7) е обединението на два интервалаи .
Отговор: ,
Пример 5Решете неравенството
. (8)
Решение. Преобразуваме неравенството (8) по следния начин:
Или .
Прилагане на интервалния метод, получаваме решение на неравенство (8).
Отговор: .
Забележка. Ако поставим и в условието на теорема 5, тогава получаваме .
Пример 6Решете неравенството
. (9)
Решение. От неравенство (9) следва. Преобразуваме неравенството (9) както следва:
Или
Тъй като , тогава или .
Отговор: .
Пример 7Решете неравенството
. (10)
Решение.Тъй като и , тогава или .
В тази връзка и неравенството (10) приема формата
Или
. (11)
От това следва, че или . Тъй като , то неравенството (11) също предполага или .
Отговор: .
Забележка. Ако приложим теорема 1 към лявата страна на неравенството (10), тогава получаваме . Оттук и от неравенство (10) следва, това или . защото, тогава неравенството (10) приема форматаили .
Пример 8Решете неравенството
. (12)
Решение.От тогава и неравенство (12) предполагаили . Въпреки това, следователно или. От тук получаваме или .
Отговор: .
Пример 9Решете неравенството
. (13)
Решение.Съгласно теорема 7, решенията на неравенство (13) са или .
Нека сега. В такъв случай и неравенството (13) приема форматаили .
Ако комбинираме интервалии , тогава получаваме решение на неравенство (13) от вида.
Пример 10Решете неравенството
. (14)
Решение.Нека пренапишем неравенство (14) в еквивалентен вид: . Ако приложим теорема 1 към лявата страна на това неравенство, тогава получаваме неравенството .
От тук и от Теорема 1 следва, че неравенството (14) е изпълнено за всякакви стойности.
Отговор: всяко число.
Пример 11.Решете неравенството
. (15)
Решение. Прилагане на теорема 1 към лявата страна на неравенството (15), получаваме . От тук и от неравенство (15) следва уравнението, което изглежда като.
Според теорема 3, уравнението е еквивалентно на неравенството. От тук получаваме.
Пример 12.Решете неравенството
. (16)
Решение. От неравенство (16), съгласно теорема 4, получаваме системата от неравенства
При решаване на неравенствотоизползваме теорема 6 и получаваме системата от неравенстваот което следва.
Помислете за неравенството. Според Теорема 7, получаваме набор от неравенстваи . Второто неравенство на населението е валидно за всяко реално.
Следователно, решението на неравенство (16) са.
Пример 13Решете неравенството
. (17)
Решение.Съгласно теорема 1 можем да напишем
(18)
Като вземем предвид неравенството (17), заключаваме, че и двете неравенства (18) се превръщат в равенства, т.е. има система от уравнения
По теорема 3 тази системауравнения е еквивалентно на системата от неравенства
или
Пример 14Решете неравенството
. (19)
Решение.От тогава . Нека умножим двете части на неравенството (19) по израза , който за всякакви стойности приема само положителни стойности. Тогава получаваме неравенство, което е еквивалентно на неравенство (19), от вида
Оттук получаваме или къде . Тъй като и тогава решенията на неравенството (19) саи .
Отговор: , .
За по-задълбочено изучаване на методите за решаване на неравенства с модул е препоръчително да се обърнете към уроци, изброени в списъка с препоръчителна литература.
1. Сборник от задачи по математика за кандидати в технически университети / Изд. M.I. Сканави. - М .: Светът и образованието, 2013. - 608 с.
2. Супрун В.П. Математика за гимназисти: методи за решаване и доказване на неравенства. – М.: Lenand / URSS, 2018. - 264 с.
3. Супрун В.П. Математика за гимназисти: нестандартни методи за решаване на задачи. - М .: КД "Либроком" / URSS, 2017. - 296 с.
Имате ли някакви въпроси?
За да получите помощта на преподавател - регистрирайте се.
сайт, с пълно или частично копиране на материала, връзката към източника е задължителна.