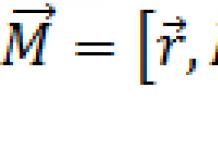Zo všetkých druhov rotačného pohybu budeme uvažovať iba rotáciu telesa okolo pevnej osi.
Moment sily
Moment sily, veličina charakterizujúca rotačný účinok sily pri pôsobení na pevné teleso; je jedným zo základných pojmov mechaniky. Rozlišovať moment moci vzhľadom k stredu (bod pólu) a relatívne k osi.
moment sily ( synonymá: krútiaci moment, krútiaci moment, krútiaci moment, krútiaci moment) vzhľadom na pevný bod 0(palice) nazývaná vektorová veličina rovná polomeru vektorového súčinu– vektor nakreslený z bodu 0 (palice) do bodu A pôsobenia sily, na vektor sily : 
.
,
kde: – moment sily, – použitá sila, – vzdialenosť od stredu otáčania k miestu pôsobenia sily, .
– rameno sily, t.j. dĺžka kolmice spustenej od stredu otáčania k čiare pôsobenia sily, je uhol medzi vektorom sily a vektorom polohy. Tie. Číselne sa moment sily rovná súčinu modulu sily na ramene .
Smer momentu sily možno určiť aj pravidlom ľavej ruky: štyri prsty ľavej ruky položte v smere prvého činiteľa, druhý činiteľ sa dostane do dlane, palec ohnutý do pravého uhla naznačí smer momentu sily. Vektor momentu sily je vždy kolmý na rovinu, v ktorej vektory a ležia.
 Ryža. 68. |
Okamih sily vzhľadom na pevnú os nazývaná skalárna veličina rovnajúca sa priemetu na túto os vektora momentu sily , definovaný vzhľadom na ľubovoľný bod danej osi(obr. 68). Moment sily vzhľadom na os je množstvo algebraické .
Pomocou pojmu moment sily môžeme novým spôsobom formulovať podmienky rovnováhy telesa fixovaného na osi. Tento stav sa nazýva pravidlo momentov: ak na teleso upevnené na osi pôsobí veľa síl, potom aby bolo teleso upevnené na osi v rovnováhe, musí byť algebraický súčet momentov všetkých síl pôsobiacich na teleso rovný nule.:
 Ryža. 69. |
Príklady:
1). kľúč
 Ryža. 70. |
2). Nech na teleso pôsobí sila v rovine kolmej na os otáčania. Rozložme túto silu na dve zložky: a (obr. 70).
Sila prechádza osou otáčania a preto neovplyvňuje otáčanie telesa. Pod vplyvom súčiastky bude telo vykonávať rotačný pohyb okolo osi. Vzdialenosť od osi otáčania k priamke, pozdĺž ktorej sila pôsobí, sa nazýva rameno sily. Moment sily vzhľadom na bod 0 je súčinom modulu sily a ramena: .
Berúc do úvahy, že moment sily 
Z hľadiska vektorovej algebry tento výraz predstavuje vektorový súčin vektora polomeru nakresleného do bodu pôsobenia sily a tejto sily.
Moment sily vo vzťahu k bodu 0 je teda vektorová veličina a rovná sa: .
Vektor momentu sily smeruje kolmo na rovinu vedenú cez vektory a a tvorí s nimi pravostrannú trojicu vektorov (pri pozorovaní z vrchu vektora je jasné, že rotácia po najkratšej vzdialenosti od k nastáva proti smeru hodinových ručičiek).
Príklady:
1). Páky
Páka je tuhé teleso, ktoré má pevnú os otáčania a je vystavené silám, ktoré ju majú tendenciu otáčať okolo tejto osi.
Príkladmi pák sú kľúče, rôzne pedále, luskáčiky, dvere atď.
Podľa pravidla momentov je páka (akákoľvek) vyvážená len vtedy . Od a , dostaneme . Z posledného vzorca vyplýva, že:
t.j. keď je páka v rovnováhe pri pôsobení dvoch síl, moduly týchto síl sú nepriamo úmerné ich ramenám. Tie. pomocou páky, čím väčší je pákový pomer, tým väčší je zisk na sile. V praxi sa to široko používa.
2). Pár síl
 Ryža. 71. |
Dve antiparalelné sily rovnakej veľkosti pôsobiace na teleso v rôznych bodoch sa nazývajú dvojice síl. Príkladom dvojice síl sú sily, ktoré pôsobia na volant automobilu (obr. 71 A), elektrické sily pôsobiace na dipól (obr. 71 b), magnetické sily pôsobiace na magnetickú strelku (obr. 71 V) atď.
Dvojica síl nemá výslednicu, to znamená, že spoločné pôsobenie týchto síl nemožno nahradiť pôsobením jednej sily. Dvojica síl teda nemôže spôsobiť translačný pohyb telesa, ale spôsobí len jeho rotáciu.
Ak sa pri otáčaní telesa vplyvom dvojice síl smery týchto síl nemenia (obr. 71 b, c), potom dochádza k rotácii telesa, kým obe sily nepôsobia proti sebe pozdĺž priamky prechádzajúcej osou rotácie telesa.
Nechajme dvojicu síl a pôsobia na teleso, ktoré má pevnú os otáčania O. Momenty týchto síl a (obr. 72). Súčet momentov 
, teda telo nie je v rovnováhe.
 Ryža. 72. |
Ak na teleso, ktoré nemá pevnú os otáčania, pôsobí dvojica síl, spôsobí otáčanie tohto telesa okolo osi prechádzajúcej ťažiskom tohto telesa.
Spád
Moment hybnosti (kinetický moment, moment hybnosti, orbitálny moment, moment hybnosti) charakterizuje množstvo rotačného pohybu. Množstvo, ktoré závisí od toho, koľko hmoty sa otáča, ako je rozložená vzhľadom na os rotácie a akou rýchlosťou rotácia nastáva.
Treba poznamenať, že rotácia je tu chápaná v širokom zmysle, nielen ako pravidelná rotácia okolo osi. Napríklad, aj keď sa teleso pohybuje po priamke za ľubovoľný imaginárny bod, ktorý neleží na pohybovej línii, má tiež moment hybnosti. Azda najväčšiu úlohu zohráva moment hybnosti pri popise skutočného rotačného pohybu. Je to však mimoriadne dôležité pre oveľa širšiu triedu problémov (najmä ak má problém stredovú alebo osovú symetriu, ale nielen v týchto prípadoch).
 Ryža. 73. |
Spád hmotný bod vzhľadom na nejaký pôvod(takže – pól) je určený vektorovým súčinom jeho polomerového vektora a impulz(Obr. 73):
,
kde je vektor polomeru častice vzhľadom na vybraný referenčný bod, ktorý je v danej referenčnej sústave stacionárny, a je hybnosť častice.
Modul momentu hybnosti sa rovná: 
, kde – rameno pulzu, bod 0 – pól, bod –
bod aplikácie impulzného vektora.
Keďže moment hybnosti je určený vektorovým súčinom, je to pseudovektor kolmý na vektory a . V prípadoch rotácie okolo konštantnej osi je však vhodné považovať nie moment hybnosti za pseudovektor, ale jeho priemet na os rotácie ako skalár, ktorého znamienko závisí od smeru rotácie.
Ak sa vyberie takáto os prechádzajúca počiatkom, na výpočet projekcie momentu hybnosti na ňu je možné špecifikovať niekoľko techník v súlade so všeobecnými pravidlami na nájdenie vektorového súčinu dvoch vektorov:
,
 Ryža. 74. |
kde je uhol medzi a , určený tak, že rotácia od do sa vykonáva proti smeru hodinových ručičiek z pohľadu pozorovateľa umiestneného na kladnej časti osi rotácie (obr. 74). Smer otáčania je pri výpočte dôležitý, pretože určuje znamienko požadovanej projekcie.
Z definície momentu hybnosti vyplýva, že je aditívny. Pre niekoľko častíc je moment hybnosti definovaný ako (vektorový) súčet nasledujúcich pojmov: , kde a sú vektor polomeru a hybnosť každej častice zahrnutej v systéme, ktorej moment hybnosti je určený. V prípade tuhého telesa sa problém redukuje na integráciu: .
Príklad:
Hybnosť hmotného bodu , rotujúceho po kružnici s polomerom (obr. 75): .
Najdôležitejším prírodným zákonom je zákon zachovania momentu hybnosti :v inerciálnej referenčnej sústave zostáva moment hybnosti uzavretého systému častíc konštantný: .
Ako dokazuje moderná fyzika (teorém E. Noethera), zákon zachovania momentu hybnosti je dôsledkom izotropia priestoru.
Moment zotrvačnosti
Je známe, že keď sa pevné teleso otáča, získava určitú stabilitu (kotúľajúca sa minca, obruč).
Analogicky s prvým Newtonovým zákonom môžeme povedať:
Tuhé teleso rotujúce okolo určitých osí prechádzajúcich ťažiskom nepodlieha pôsobeniu vonkajších síl a rotáciu si zachováva donekonečna.
 Ryža. 76. |
Nechajte hmotný bod rotovať po kružnici s polomerom pod vplyvom sily (obr. 76).
Potom podľa druhého Newtonovho zákona: , , kde je uhlové zrýchlenie bodu; z toho vyplýva: , kde je moment sily vzhľadom na os otáčania.
Označme: 
– moment zotrvačnosti bodu otáčania.
Potom moment sily pôsobiacej na bod: .
Moment zotrvačnosti telesa vzhľadom na os rotácie sa rovná súčtu momentov zotrvačnosti všetkých jeho bodov: 
. Matematicky sa problém týka integrácie.
Moment zotrvačnostiI–skalárna veličina, ktorá charakterizuje rozloženie hmoty v telese a je spolu s hmotnosťou mierou zotrvačnosti telesa pri rotačnom pohybe.
To isté teleso môže mať rôzne momenty zotrvačnosti okolo rôznych osí.
Pre daný smer osi vzhľadom na teleso bude moment zotrvačnosti telesa vzhľadom na túto os najmenší, ak os prechádza ťažiskom telesa(T. S), t.j. .
Medzi osami prechádzajúcimi ťažiskom telesa sú tri špeciálne na seba kolmé osi. Pri rovnomernom otáčaní okolo týchto osí nemá teleso žiadny vplyv na ložiská. Tieto osi sú tzv hlavné osi. S ľubovoľným tvarom tela je ťažké ich nájsť. Ale pre symetrické telesá je poloha hlavných osí ľahko určená. Momenty zotrvačnosti telesa vzhľadom na hlavné osi sa nazývajú hlavné momenty zotrvačnosti.
Hlavné momenty zotrvačnosti telies jednoduchého tvaru
| Momenty zotrvačnosti homogénnych telies najjednoduchšieho tvaru vzhľadom na určité osi otáčania | |||
| Telo | Popis | Poloha osi a | Moment zotrvačnosti |
 | Hmotná bodová hmotnosť m | Na diaľku r z bodu, stacionárne | |
 | Dutý tenkostenný valec alebo polomerový krúžok r a omše m | Os valca | |
 | Pevný valec alebo polomerový disk r a omše m | Os valca | |
 | Dutý hrubostenný masový valec m s vonkajším polomerom r 2 a vnútorný polomer r 1(rúra) | Os valca | |
 | l a omše m | Os je kolmá na tyč a prechádza jej ťažiskom | |
 | Rovná tenká tyč l a omše m | Os je kolmá na tyč a prechádza jej koncom | |
 | Tenkostenná guľa s polomerom r a omše m | Os prechádza stredom gule | |
 | Polomerová guľa r a omše m | Os prechádza stredom lopty |
Steinerova veta
Moment zotrvačnosti telesa vzhľadom na ľubovoľnú os je určený Steinerovou vetou:
 Ryža. 77. |
Moment zotrvačnosti tela vzhľadom na ľubovoľnú os sa rovná súčtu momentu zotrvačnosti vzhľadom na os,rovnobežný s daným a prechádzajúci stredom zotrvačnosti telesa, súčin telesnej hmotnosti krát druhá mocnina vzdialenosti medzi osami(obr. 77).
kde je ľubovoľná os, je vzdialenosť medzi osami.
Matematická formulácia Steinerovej vety: 
, kde je telesná hmotnosť.
Príklad.
Moment zotrvačnosti tyče vzhľadom k osi prechádzajúcej jej koncom sa rovná:
kde je moment zotrvačnosti tyče voči osi prechádzajúcej ťažiskom tyče.
Rovnica pre dynamiku rotačného pohybu tuhého telesa vzhľadom na pevnú os
Z predchádzajúceho odseku ( Moment zotrvačnosti) z toho vyplýva, že pre ten hmotný bod rotujúci po kružnici platí vzťah: .
Pre pevné teleso pozostávajúce z hmotných bodov: 
; ,dostaneme: .
Rovnica (1) je rovnica dynamiky rotujúceho tuhého telesa (základná rovnica dynamiky rotačného pohybu):
Uhlové zrýchlenie tuhého telesa, otáčanie okolo pevnej osi, priamo úmerné celkovému momentu všetkých vonkajších síl, pôsobiace na telo, a nepriamo úmerné jeho momentu zotrvačnosti.
Uveďme rovnicu (1) ako:
Berúc do úvahy skutočnosť, že 
, kde je moment hybnosti telesa. Potom: . (2)
Rovnica (2) je tiež rovnicou dynamiky rotujúceho tuhého telesa (základná rovnica dynamiky rotačného pohybu):
Rýchlosť zmeny momentu hybnosti telesa vzhľadom na určitú os sa rovná výslednému momentu vzhľadom na rovnakú os všetkých vonkajších síl, pripevnený k telu.
Z rovníc (1) a (2) vyplýva: 
.
Potom dostaneme: . (3)
 Ryža. 78. |
Ak je sústava častíc uzavretá, tak na ňu nepôsobia vonkajšie sily, potom moment vonkajších síl, t.j. získa sa zákon zachovania hybnosti. Ak vezmeme do úvahy rovnicu (3), dostaneme:
. To znamená, že uhlová rýchlosť je nepriamo úmerná momentu zotrvačnosti telesa (pozri obr. 78). Podobná vlastnosť sa používa, keď krasokorčuliari predvádzajú hody na ľade, saltá akrobatov.
Kinetická energia rotujúceho tuhého telesa
Rotujúce tuhé teleso má energiu.
Keď sa tuhé teleso otáča vzhľadom na pevnú os, jeho jednotlivé hmotové prvky opisujú kružnice s rôznymi polomermi a majú rôzne lineárne rýchlosti. Uhlová rýchlosť otáčania všetkých bodov tela je však rovnaká:
.
Kinetická energia telesa je súčtom kinetických energií všetkých jeho telies:
.Pretože , potom dostaneme:
Zoberme si, že moment zotrvačnosti telesa sa rovná súčtu momentov zotrvačnosti všetkých jeho bodov: 
.
Ak vezmeme do úvahy posledný vzťah, získame konečný výraz pre kinetickú energiu rotujúceho tuhého telesa:
V prípade rovinného pohybu tuhého telesa sa jeho celková kinetická energia rovná:
.
Analógia medzi translačným a rotačným pohybom
Medzi pohybom tuhého telesa okolo pevnej osi a pohybom jednotlivého hmotného bodu (alebo translačným pohybom telesa) existuje blízka a ďalekosiahla analógia. Každá lineárna veličina z kinematiky bodu zodpovedá podobnej veličine z kinematiky rotácie tuhého telesa. Súradnica zodpovedá uhlu, lineárnej rýchlosti , uhlová rýchlosť, lineárne (tangenciálne) zrýchlenie – uhlové zrýchlenie.
| Pohyb vpred | Rotačný pohyb | ||||
| Kinematické charakteristiky pohybu | |||||
| Cesta | S | m | Uhol natočenia | j | rád |
| Čas | t | s | Obdobie | T | s |
| Rýchlosť | pani | Uhlová rýchlosť | w | rad/s | |
| Zrýchlenie | a | m/s 2 | Uhlové zrýchlenie | e | rad/s 2 |
| Dynamické jazdné vlastnosti | |||||
| Hmotnosť | m | kg | Moment zotrvačnosti | J | kg × m 2 |
| sila | F | N | Moment sily | M | N × m |
| Pulz | P | kg × m/s | Spád | L=Jx w | kg × m2/s |
| Druhý Newtonov zákon | F=ma; F=dp/dt | Rovnica dynamiky rotačného pohybu | M=Jxe; M = dl/dt | ||
| Job | dA=FxdS | J | Job | dA=M×dj | J |
| Kinetická energia | E K = (m 2)/2 | J | Kinetická energia | EK BP = (J w 2)/2 | J |
| Moc | N=F | W | Moc | N=Mx w | W |
Translačný pohyb možno považovať za rotačný, pričom polomer otáčania má tendenciu k nekonečnu a uhlová rýchlosť má tendenciu k nule.
 Ryža. 79. |
5. Mechanický (klasický) princíp relativity
(Galileov princíp relativity)
Stručný životopis G. Galilea
GALILEO Galileo(15.II.1564 - 8.I.1642) - vynikajúci taliansky fyzik a astronóm, jeden zo zakladateľov exaktných prírodných vied, člen Académie de Lince (1611), narodený v Pise. V roku 1581 vstúpil na univerzitu v Pise, kde študoval medicínu. Ale fascinovaný geometriou a mechanikou, najmä prácami Archimeda a Euklida, opustil univerzitu s jej školskými prednáškami a vrátil sa do Florencie, kde štyri roky študoval matematiku sám.
Od roku 1589 - profesor na univerzite v Pise, v rokoch 1592-1610 - na univerzite v Padove, neskôr - dvorný filozof vojvodu Cosima II de' Medici.
Mal významný vplyv na rozvoj vedeckého myslenia. Z neho pochádza fyzika ako veda. Ľudstvo vďačí Galileovi za dva princípy mechaniky, ktoré zohrali veľkú úlohu vo vývoji nielen mechaniky, ale aj celej fyziky. Ide o známy Galileov princíp relativity pre priamočiary a rovnomerný pohyb a princíp nemennosti gravitačného zrýchlenia.
Galileo zaviedol zákon zotrvačnosti (1609), zákony voľného pádu, pohybu telesa po naklonenej rovine (1604 - 09) a telesa hodeného pod uhlom k horizontu, objavil zákon sčítania pohybov a tzv. zákon stálosti periódy kmitania kyvadla (fenomén izochronizmu kmitov, 1583). Dynamika pochádza z Galilea.
V júli 1609 Galileo zostrojil svoj prvý ďalekohľad – optický systém pozostávajúci z konvexnej a konkávnej šošovky – a začal so systematickými astronomickými pozorovaniami. To bolo znovuzrodenie ďalekohľadu, ktorý sa po takmer 20 rokoch nejasností stal mocným nástrojom vedeckého poznania. Preto možno Galilea považovať za vynálezcu prvého ďalekohľadu. Svoj teleskop rýchlo zdokonalil, a ako časom napísal, „zostrojil si zariadenie také úžasné, že s jeho pomocou sa predmety zdali takmer tisíckrát väčšie a viac ako tridsaťkrát bližšie, než keď sa pozorovali jednoduchým okom“. V pojednaní „Hviezdny posol“, publikovanom v Benátkach 12. marca 1610, opísal objavy uskutočnené pomocou ďalekohľadu: objavenie hôr na Mesiaci, štyroch satelitov Jupitera, dôkaz, že Mliečna dráha pozostáva z veľa hviezd.
Galileiho astronomické objavy zohrali obrovskú úlohu vo vývoji vedeckého svetonázoru, jasne presvedčili o správnosti Kopernikovho učenia, omyle systému Aristotela a Ptolemaia a prispeli k víťazstvu a vytvoreniu heliocentrického systému r. sveta. V roku 1632 vyšiel slávny „Dialóg o dvoch hlavných systémoch sveta“, v ktorom Galileo obhajoval heliocentrický systém Koperníka. Vydanie knihy rozzúrilo duchovenstvo, inkvizícia obvinila Galilea z kacírstva a po zorganizovaní procesu ho prinútila verejne sa zriecť koperníkovského učenia a zakázala Dialóg. Po procese v roku 1633 bol Galileo vyhlásený za „väzňa Svätej inkvizície“ a bol nútený žiť najskôr v Ríme a potom v Archertri pri Florencii. Galileo však svoju vedeckú činnosť nezastavil, pred chorobou (v roku 1637 Galileo definitívne prišiel o zrak) dokončil prácu „Rozhovory a matematické dôkazy o dvoch nových odvetviach vedy“, ktorá zhŕňala jeho fyzikálne výskumy.
Vynašiel termoskop, ktorý je prototypom teplomera, navrhol (1586) hydrostatické váhy na určenie špecifickej hmotnosti pevných látok a určil špecifickú hmotnosť vzduchu. Predložil myšlienku použitia kyvadla v hodinách. Fyzikálny výskum sa venuje aj hydrostatike, pevnosti materiálov a pod.
Eseje:
1. Dialóg o dvoch najvýznamnejších systémoch sveta, Ptolemaiovom a Kopernikovom. M.–L. OGIZ, 1948.
2. Assay master / Transl. Yu.A. Danilova. – M.: Nauka, 1987. – 272 s. – (Séria „Populárne diela klasikov prírodných vied“).
3. Rozhovory a matematické dôkazy týkajúce sa dvoch nových vedných odborov (Diela, zväzok 1). GTTI. M–L. 1934.
4. Úvahy o telách plávajúcich vo vode ao tých, ktoré sa v nej pohybujú V ČT: Archimedes. Stavin. Galileo. Pascal.Začiatok gyrostatiky. Séria "Klasika prírodných vied"" GNTTI. M.-L. 1933.
Mechanický princíp relativity
Princíp relativity je princíp rovnosti inerciálnych referenčných systémov (IRS) v klasickej mechanike, ktorý sa prejavuje tým, že zákony mechaniky sú vo všetkých takýchto systémoch rovnaké, stanovil G. Galileo v roku 1636.
Galileo ilustroval zhodnosť zákonov mechaniky pre inerciálne sústavy na príklade javov vyskytujúcich sa pod palubou lode v pokoji alebo pohybujúcich sa rovnomerne a priamočiaro (vzhľadom na Zem, ktorú možno s dostatočnou presnosťou považovať za inerciálnu referenčný rámec): „Teraz dajte loď do pohybu akoukoľvek rýchlosťou a potom (pokiaľ je pohyb rovnomerný a bez kývania jedným alebo druhým smerom) vo všetkých uvedených javoch nenájdete najmenšiu zmenu a žiadny z nich budete vedieť určiť, či sa loď pohybuje alebo stojí na mieste... Keď hodíte nejakú vec súdruhovi, nebudete ju musieť hádzať väčšou silou, keď je on na prove a vy na korme, ako keď sú vaše relatívne pozície sú obrátené; Kvapky, ako predtým, padnú do spodnej časti plavidla a ani jedna nepadne bližšie k korme, hoci kým je kvapka vo vzduchu, loď prejde mnoho rozpätí“ („Dialóg o dvoch najdôležitejších systémoch svet, Ptolemaiov a Kopernikov,“ M. – L., 1948, s. 147).
Relatívny pohyb hmotného bodu: jeho poloha, rýchlosť, typ trajektórie závisí od toho, ku ktorému referenčnému systému (referenčnému telesu) sa tento pohyb považuje. Zároveň platí, že zákony klasickej mechaniky, teda vzťahy, ktoré spájajú veličiny opisujúce pohyb hmotných bodov a vzájomné pôsobenie medzi nimi, sú vo všetkých inerciálnych vzťažných sústavách rovnaké. Relativita mechanického pohybu a rovnakosť (nepodstatnosť) zákonov mechaniky v rôznych inerciálnych vzťažných sústavách tvoria obsah Galileovho princípu relativity, ktorý logicky vyplýva zo známych Galileových transformácií.
Galileiho premeny– v klasickej mechanike transformácie súradníc a rýchlosti pri prechode z jednej inerciálnej vzťažnej sústavy(ISO)inému.
Tieto transformácie sú platné iba pri rýchlostiach oveľa menších ako je rýchlosť svetla vo vákuu a sú založené na dvoch predpokladoch, ktoré boli implicitne prijaté a boli považované za zrejmé:
Beh času je rovnaký vo všetkých inerciálnych referenčných sústavách;
Lineárne rozmery telesa nezávisia od rýchlosti jeho pohybu vzhľadom na referenčný systém.
 Ryža. 80. |
Nech existujú dva inerciálne referenčné systémy, z ktorých jeden, , súhlasíme s tým, že budeme uvažovať v pokoji; druhý systém, sa pohybuje vzhľadom na konštantnú rýchlosť, ako je znázornené na obr. 80.
Potom majú galilejské premeny tvar:
alebo pomocou vektorovej notácie,
(posledný vzorec zostáva pravdivý pre akýkoľvek smer súradnicových osí).
Z Galileových transformácií vyplýva:
Klasický zákon sčítania rýchlostí: kde je rýchlosť bodu M v „pevnom“ referenčnom rámci, ’ – rýchlosť bodu M v pohybujúcom sa systéme;
Nemennosť (stálosť) zrýchlenia bodu M a sily, ktoré naň pôsobia:
Z posledných vzťahov vyplýva, že rovnica druhého Newtonovho zákona sa pri prechode z jedného ISO na druhé nemení, t.j. Newtonove zákony sú invariantné ku Galileovým transformáciám.
Moderné formulácie klasického princípu relativity:
1). Vo všetkých ISO za rovnakých podmienok sa všetky mechanické javy vyskytujú rovnakým spôsobom.
2). Zákony klasickej mechaniky sú invariantné vzhľadom na prechod z jedného ISO do druhého.
V modernej fyzike sa ukazuje, že klasický princíp relativity naznačuje, že všetky ISO sú rovnaké, neexistuje žiadny „absolútny“ referenčný rámec.
Galileov princíp relativity platí len v klasickej mechanike, ktorá uvažuje o pohyboch s rýchlosťami oveľa nižšími ako je rýchlosť svetla. Pri rýchlostiach blízkych rýchlosti svetla sa pohyb telies riadi Einsteinovými zákonmi relativistickej mechaniky , ktoré sú invariantné vzhľadom na ostatné transformácie súradníc a Lorentzovho času. Jeden z postulátov špeciálnej teórie sformuloval Einstein relativistický princíp relativity: fyzikálne zákony sú invariantné vzhľadom na prechod z jedného ISO do druhého.
Osnova prednášky
Moment zotrvačnosti.
Moment sily. Základná rovnica dynamiky rotačného pohybu.
Okamih impulzu. Zákon zachovania momentu hybnosti.
Práca a kinetická energia pri rotačnom pohybe.
Moment zotrvačnosti.
Pri uvažovaní o rotačnom pohybe je potrebné zaviesť nové fyzikálne pojmy: moment zotrvačnosti, moment sily, moment impulzu.
Moment zotrvačnosti je miera zotrvačnosti telesa počas rotačného pohybu telesa.
Moment zotrvačnosti hmotného bodu vzhľadom na pevnú os otáčania sa rovná súčinu jeho hmotnosti so štvorcom vzdialenosti od uvažovanej osi otáčania (obr. 1):
závisí iba od hmotnosti hmotného bodu a jeho polohy vzhľadom na os rotácie a nezávisí od prítomnosti samotnej rotácie.
Moment zotrvačnosti je skalárna a aditívna veličina, preto sa moment zotrvačnosti telesa rovná súčtu momentov zotrvačnosti všetkých jeho bodov:
.
V prípade spojitého rozdelenia hmoty sa tento súčet redukuje na integrál:
,
kde je hmotnosť malého objemu telesa 
,
- hustota tela, 
- vzdialenosť od prvku 
k osi otáčania.
Moment zotrvačnosti je analógom hmoty počas rotačného pohybu. Čím väčší je moment zotrvačnosti telesa, tým ťažšie je meniť uhlovú rýchlosť rotujúceho telesa. Moment zotrvačnosti má zmysel len pre danú polohu osi otáčania. Nemá zmysel hovoriť jednoducho o „momente zotrvačnosti“. Záleží:
1) z polohy osi otáčania;
2) z rozloženia telesnej hmoty vzhľadom na os rotácie, t.j. na tvare tela a jeho veľkosti.
Experimentálnym dôkazom toho je experiment s valcovacími valcami.
Integráciou pre niektoré homogénne telesá môžeme získať nasledujúce vzorce (os rotácie prechádza ťažiskom telesa).
Moment zotrvačnosti obruče (hrúbku steny zanedbávame) alebo dutého valca:
Moment zotrvačnosti disku alebo plného valca s polomerom R:
.
Moment zotrvačnosti lopty
Moment zotrvačnosti tyče
E 
Ak je pre teleso známy moment zotrvačnosti okolo osi prechádzajúcej cez ťažisko, potom moment zotrvačnosti okolo ktorejkoľvek osi rovnobežnej s prvou sa zistí podľa Steinerova veta: moment zotrvačnosti telesa voči ľubovoľnej osi sa rovná momentu zotrvačnosti J 0 voči osi rovnobežnej s danou a prechádzajúcej ťažiskom telesa, pripočítaný k súčinu hmotnosti telesa a štvorec vzdialenosti medzi osami.
Kde d vzdialenosť od ťažiska O k osi otáčania (obr. 2).
Ťažisko- pomyselný bod, ktorého poloha charakterizuje rozloženie hmoty daného telesa. Ťažisko telesa sa pohybuje rovnako, ako by sa pohyboval hmotný bod rovnakej hmotnosti pod vplyvom všetkých vonkajších síl pôsobiacich na dané teleso.
Pojem moment zotrvačnosti zaviedol do mechaniky domáci vedec L. Euler v polovici 18. storočia a odvtedy je široko používaný pri riešení mnohých problémov dynamiky tuhého telesa. Hodnota momentu zotrvačnosti musí byť v praxi známa pri výpočte rôznych rotačných komponentov a systémov (zotrvačníky, turbíny, rotory elektromotorov, gyroskopy). Moment zotrvačnosti je zahrnutý v pohybových rovniciach telesa (loď, lietadlo, projektil atď.). Zisťuje sa, keď niekto chce poznať parametre rotačného pohybu lietadla okolo ťažiska pod vplyvom vonkajšej poruchy (náryv vetra a pod.).
4.6 Rotačný pohyb tuhého telesa. Moment sily.
Samozrejme, poloha jedného, hoci aj „špeciálneho“ bodu úplne nevystihuje pohyb celej uvažovanej sústavy telies, ale predsa len je lepšie poznať polohu aspoň jedného bodu, ako nevedieť nič. Uvažujme však o aplikácii Newtonových zákonov na popis rotácie tuhého telesa okolo pevnej osi.
Začnime s najjednoduchším prípadom: nech hmotný bod m pripevnený beztiažovou tuhou tyčou r k pevnej osi OO'(obr. 46). Hmotný bod sa môže pohybovať okolo osi a zostáva od nej v konštantnej vzdialenosti, preto bude jeho trajektóriou kruh so stredom na osi rotácie.
Samozrejme, že pohyb bodu sa riadi rovnicou druhého Newtonovho zákona \(~m \vec a = \vec F_0\). Priama aplikácia tejto rovnice však nie je opodstatnená: po prvé, bod má jeden stupeň voľnosti, preto je vhodné použiť uhol natočenia ako jedinú súradnicu, a nie dve karteziánske súradnice; po druhé, na uvažovaný systém pôsobia reakčné sily v osi otáčania a priamo na materiálový bod ťažná sila tyče. Hľadanie týchto síl je samostatný problém, ktorého riešenie je zbytočné popisovať rotáciu. Preto má zmysel získať na základe Newtonových zákonov špeciálnu rovnicu, ktorá priamo popisuje rotačný pohyb.
Nech v určitom okamihu pôsobí určitá sila \(~\vec F\) na hmotný bod ležiaci v rovine kolmej na os otáčania (obr. 47). Pri kinematickom popise krivočiareho pohybu sa vektor celkového zrýchlenia \(~\vec a\) vhodne rozloží na dve zložky: normálnu \(~\vec a_n\), smerujúcu k osi rotácie, a tangenciálnu \(~\ vec a_(\tau)\ ) nasmerovaná rovnobežne s vektorom rýchlosti. Na určenie pohybového zákona nepotrebujeme hodnotu normálneho zrýchlenia. Samozrejme, toto zrýchlenie je spôsobené aj pôsobiacimi silami, z ktorých jednou je neznáma napínacia sila tyče.
Napíšme rovnicu druhého zákona v projekcii na tangenciálny smer:
\(~m a_(\tau) = F_(\tau)\) , (1)
Všimnite si, že reakčná sila tyče nie je zahrnutá v tejto rovnici, pretože je nasmerovaná pozdĺž tyče a kolmo na zvolenú projekciu. Zmena uhla natočenia φ je priamo určená uhlovou rýchlosťou \(~\omega = \frac(\Delta \varphi)(\Delta t)\), ktorej zmenu zasa popisuje uhlové zrýchlenie \(~\varepsilon = \frac( \Delta \omega)(\ Delta t)\) . Uhlové zrýchlenie súvisí s tangenciálnou zložkou zrýchlenia vzťahom a τ = rε. Ak tento výraz dosadíme do rovnice (9), dostaneme rovnicu vhodnú na určenie uhlového zrýchlenia. Je vhodné zaviesť novú fyzikálnu veličinu, ktorá určuje interakciu telies pri ich rotácii. Ak to chcete urobiť, vynásobte obe strany rovnice (1). r
\(~m r^2 \varepsilon = F_(\tau) r\) . (2)
a zvážte výraz na jeho pravej strane F τ r, ktorý má význam súčinu tangenciálnej zložky sily a vzdialenosti od osi otáčania k bodu pôsobenia sily. Rovnaké dielo môže byť prezentované v mierne odlišnej podobe (pozri obr. 48)
M = F τ r = O cos α = Fd, Tu d- vzdialenosť od osi otáčania k čiare pôsobenia sily, ktorá je aj tzv rameno sily. Táto fyzikálna veličina súčin modulu sily a vzdialenosti od čiary pôsobenia sily k osi otáčania (rameno sily) M = Fd nazývaný moment sily. Pôsobenie sily môže viesť k rotácii v smere aj proti smeru hodinových ručičiek. V súlade so zvoleným kladným smerom otáčania by sa malo určiť znamienko momentu sily. Všimnite si, že moment sily je určený tou zložkou sily, ktorá je kolmá na vektor polomeru bodu aplikácie. Zložka vektora sily smerujúca pozdĺž segmentu spájajúceho miesto pôsobenia a os rotácie nevedie k rozkrúteniu telesa. Keď je os pevná, táto zložka je kompenzovaná reakčnou silou v osi, takže neovplyvňuje otáčanie telesa.
Napíšme si ešte jeden užitočný výraz pre moment sily. Nech sila \(~\vec F\) pôsobí na bod A , ktorých karteziánske súradnice sú rovnaké X,r(obr. 49). Rozložme silu \(~\vec F\) na dve zložky \(~\vec F_x, \vec F_y\) rovnobežné s príslušnými súradnicovými osami. Moment sily \(~\vec F\) vo vzťahu k osi prechádzajúcej počiatkom súradníc sa zjavne rovná súčtu momentov zložiek \(~\vec F_x, \vec F_y\), tj. M = xF y- yF X.
Rovnakým spôsobom, ako sme zaviedli koncept vektora uhlovej rýchlosti, môžeme definovať aj koncept vektora krútiaceho momentu. Modul tohto vektora zodpovedá definícii uvedenej vyššie a je nasmerovaný kolmo na rovinu obsahujúcu vektor sily a segment spájajúci miesto pôsobenia sily s osou rotácie. Vektor momentu sily možno definovať aj ako vektorový súčin vektora polomeru bodu pôsobenia sily a vektora sily
\(~\vec M = \vec r \krát \vec F\) .
Všimnite si, že keď sa bod pôsobenia sily posunie pozdĺž línie jej pôsobenia, moment sily sa nemení.
Označme súčin hmotnosti hmotného bodu druhou mocninou vzdialenosti k osi rotácie Pán 2 = ja(toto množstvo sa nazýva moment zotrvačnosti hmotného bodu vzhľadom na os). Použitím týchto zápisov nadobudne rovnica (2) formu, ktorá sa formálne zhoduje s rovnicou druhého Newtonovho zákona pre translačný pohyb.
\(~I \varepsilon = M\) . (3)
Táto rovnica sa nazýva základná rovnica dynamiky rotačného pohybu. Moment sily v rotačnom pohybe teda hrá rovnakú úlohu ako sila v translačnom pohybe; je to ten, ktorý určuje zmenu uhlovej rýchlosti. Ukazuje sa (a to potvrdzuje naša každodenná skúsenosť), že vplyv sily na rýchlosť otáčania je určený nielen veľkosťou sily, ale aj miestom jej pôsobenia. Moment zotrvačnosti určuje zotrvačné vlastnosti telesa vo vzťahu k rotácii (zjednodušene povedané, ukazuje, či je ľahké teleso roztočiť) - čím ďalej je hmotný bod od osi rotácie, tým ťažšie je uveďte ho do rotácie.
Rovnicu (3) možno zovšeobecniť na prípad rotácie ľubovoľného telesa. Keď sa teleso otáča okolo pevnej osi, uhlové zrýchlenia všetkých bodov telesa sú rovnaké. Preto, podobne ako pri odvodzovaní Newtonovej rovnice pre translačný pohyb telesa, môžeme napísať rovnice (3) pre všetky body rotujúceho telesa a potom ich sčítať. V dôsledku toho získame rovnicu, ktorá sa externe zhoduje s (3), v ktorej ja- moment zotrvačnosti celého telesa rovný súčtu momentov jeho základných hmotných bodov, M- súčet momentov vonkajších síl pôsobiacich na teleso.
Ukážme si, ako sa vypočíta moment zotrvačnosti telesa. Je dôležité zdôrazniť, že moment zotrvačnosti telesa závisí nielen od hmotnosti, tvaru a veľkosti telesa, ale aj od polohy a orientácie osi otáčania. Formálne postup výpočtu spočíva v rozdelení telesa na malé časti, ktoré možno považovať za hmotné body (obr. 51), a sčítaní momentov zotrvačnosti týchto hmotných bodov, ktoré sa rovnajú súčinu hmotnosti krát štvorec vzdialenosti k osi otáčania
\(~I = m_1 r^2_1 + m_2 r^2_2 + m_3 r^2_3 + \ldots\) .
Pre telesá jednoduchého tvaru sa takéto množstvá už dlho vypočítali, takže často stačí zapamätať si (alebo nájsť v referenčnej knihe) zodpovedajúci vzorec pre požadovaný moment zotrvačnosti. Ako príklad: moment zotrvačnosti kruhového homogénneho valca s hmotnosťou m a polomer R lebo os rotácie zhodná s osou valca sa rovná \(~I = \frac(1)(2) m R^2\) .
Moment sily F, pôsobiace na teleso vzhľadom na os otáčania
,
Kde 
-
projekcia sily F v rovine kolmej na os otáčania; l - silu ramien F(najkratšia vzdialenosť od osi otáčania k čiare pôsobenia sily).
Moment zotrvačnosti okolo osi otáčania:
a) hmotný bod
J= Pán 2 ,
Kde T - hmotnosť bodu; r - jeho vzdialenosť od osi otáčania;
b) diskrétne pevné teleso
Kde 
- hmotnosť i-tý prvok tela; r i je vzdialenosť tohto prvku od osi otáčania; P
-
počet prvkov tela;
c) tuhá pevná látka
Ak je teleso homogénne, teda jeho hustota 
je potom v celom objeme rovnaký
dm=
dV A 
Kde V- telesný objem.
Momenty zotrvačnosti niektorých telies pravidelného geometrického tvaru:
|
Os, okolo ktorej sa určuje moment zotrvačnosti |
Formula Moment zotrvačnosti |
|
|
Homogénna tenká tyčinka hmoty T a dĺžka l Tenký krúžok, obruč, rádiusová rúrka R a omšu T, polomer zotrvačníka R a omšu T, rozložené pozdĺž okraja Okrúhly homogénny disk (valec) s polomerom R a omšu T Homogénna guľa hmoty T a polomer R |
Prechádza cez ťažisko tyče kolmo na tyč Prechádza koncom tyče kolmo na tyč Prechádza stredom kolmo na rovinu základne Prechádza stredom disku kolmo na rovinu základne Prihráva cez stred lopty |
1/12ml 2 |
Steinerova veta. Moment zotrvačnosti telesa okolo ľubovoľnej osi
J= J 0 + ma 2 ,
Kde J 0 - moment zotrvačnosti tohto telesa voči osi prechádzajúcej ťažiskom telesa rovnobežnej s danou osou; A - vzdialenosť medzi nápravami; m- telesná hmotnosť.
Moment hybnosti rotujúceho telesa vzhľadom na os
L=
J
.
Zákon zachovania momentu hybnosti
Kde L i - moment hybnosti i-tého telesa zahrnutého v sústave. Zákon zachovania momentu hybnosti pre dve interagujúce telesá
Kde 
- momenty zotrvačnosti a uhlové rýchlosti telies pred interakciou: 
- rovnaké hodnoty po interakcii.
Zákon zachovania momentu hybnosti pre jedno teleso, ktorého moment zotrvačnosti sa mení,
Kde 
- počiatočný a konečný moment zotrvačnosti; 
- počiatočná a konečná uhlová rýchlosť telesa.
Základná rovnica pre dynamiku rotačného pohybu tuhého telesa voči pevnej osi
M d t=d(J 
), Kde M- moment sily pôsobiacej na teleso v čase dt;
J
-
moment zotrvačnosti tela;
- uhlová rýchlosť; J
-
moment impulzu.
Ak sú moment sily a moment zotrvačnosti konštantné, potom sa táto rovnica zapíše ako
M
t=J
.
V prípade konštantného momentu zotrvačnosti má základná rovnica pre dynamiku rotačného pohybu tvar
M=J
, Kde 
- uhlové zrýchlenie.
Práca konštantného momentu sily M, pôsobiace na rotujúce teleso
kde je uhol natočenia telesa.
Okamžitá sila vyvinutá počas rotácie tela
N=
M
.
Kinetická energia rotujúceho telesa
T=1/2
J
.
Kinetická energia telesa valiaceho sa po rovine bez kĺzania je
T== 1 / 2
mv 2
+l/2 J
,
Kde l /
2
mv 2
-
kinetická energia translačného pohybu telesa; v
-
rýchlosť stredu zotrvačnosti tela; l/2 J
, je kinetická energia rotačného pohybu telesa okolo osi prechádzajúcej stredom zotrvačnosti.
Práca vykonaná pri rotácii telesa a zmena jeho kinetickej energie súvisia so vzťahom
Tuhé teleso rotujúce okolo určitých osí prechádzajúcich ťažiskom, ak je oslobodené od vonkajších vplyvov, udržiava rotáciu na neurčito. (Tento záver je podobný prvému Newtonovmu zákonu pre translačný pohyb.)
Vznik rotácie tuhého telesa je vždy spôsobený pôsobením vonkajších síl pôsobiacich na jednotlivé body telesa. V tomto prípade je nevyhnutný vznik deformácií a vznik vnútorných síl, ktoré v prípade pevného telesa zabezpečujú praktické zachovanie jeho tvaru. Keď prestane pôsobiť vonkajšie sily, rotácia sa zachová: vnútorné sily nemôžu spôsobiť ani zničiť rotáciu tuhého telesa.
Výsledkom pôsobenia vonkajšej sily na teleso s pevnou osou otáčania je zrýchlený rotačný pohyb telesa. (Tento záver je podobný druhému Newtonovmu zákonu pre translačný pohyb.)
Základný zákon dynamiky rotačného pohybu: v inerciálnej referenčnej sústave je uhlové zrýchlenie získané telesom rotujúcim okolo pevnej osi úmerné celkovému momentu všetkých vonkajších síl pôsobiacich na teleso a nepriamo úmerné momentu zotrvačnosti telesa vzhľadom na danú os :
Môže byť poskytnutá jednoduchšia formulácia základný zákon dynamiky rotačného pohybu(nazýva sa aj Druhý Newtonov zákon pre rotačný pohyb): krútiaci moment sa rovná súčinu momentu zotrvačnosti a uhlového zrýchlenia:
moment impulzu(moment hybnosti, moment hybnosti) telesa sa nazýva súčin jeho momentu zotrvačnosti a uhlovej rýchlosti:
Hybnosť je vektorová veličina. Jeho smer sa zhoduje so smerom vektora uhlovej rýchlosti.
Zmena momentu hybnosti sa určuje takto:
. (I.112)
Zmena momentu hybnosti (s konštantným momentom zotrvačnosti telesa) môže nastať len ako dôsledok zmeny uhlovej rýchlosti a je vždy dôsledkom pôsobenia momentu sily.
Podľa vzorca, ako aj vzorcov (I.110) a (I.112), môže byť zmena momentu hybnosti vyjadrená ako:
. (I.113)
Produkt vo vzorci (I.113) sa nazýva impulz hybnosti alebo hnacia sila. Rovná sa zmene momentu hybnosti.
Vzorec (I.113) platí za predpokladu, že moment sily sa časom nemení. Ak moment sily závisí od času, t.j. , To
. (I.114)
Vzorec (I.114) ukazuje, že: zmena momentu hybnosti sa rovná časovému integrálu momentu sily. Okrem toho, ak je tento vzorec uvedený vo forme: , definícia bude vyplývať z neho moment sily: Okamžitý krútiaci moment je prvou deriváciou momentu hybnosti vzhľadom na čas,
