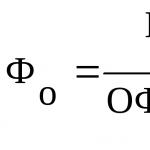Дори в училище учителите се опитаха да ни набият в главите най-простото правило: „Всяко число, умножено по нула, е равно на нула!“, - но въпреки това около него постоянно възникват много спорове. Някои хора просто си спомнят правилото и не се занимават с въпроса "защо?" „Не можеш и това е, защото така казаха в училище, правилото си е правило!“ Някой може да напълни половин тетрадка с формули, доказващи това правило или, обратно, неговата нелогичност.
Във връзка с
Кой е прав в крайна сметка?
По време на тези спорове и двамата хора с противоположни гледни точки се гледат като овен и доказват с всички сили, че са прави. Въпреки че, ако ги погледнете отстрани, можете да видите не един, а два овена, опрели рогата си един в друг. Единствената разлика между тях е, че единият е малко по-малко образован от другия.
Най-често тези, които смятат това правило за неправилно, се опитват да апелират към логиката по този начин:
Имам две ябълки на масата си, ако сложа нула ябълки върху тях, тоест не сложа нито една, тогава двете ми ябълки няма да изчезнат! Правилото е нелогично!
Наистина, ябълките няма да изчезнат никъде, но не защото правилото е нелогично, а защото тук се използва малко по-различно уравнение: 2 + 0 = 2. Така че нека отхвърлим това заключение веднага - нелогично е, въпреки че има противоположна цел - да призоваваме към логиката.
Какво е умножение
Първоначално правилото за умножениее дефинирано само за естествени числа: умножението е число, добавено към себе си определен брой пъти, което означава, че числото е естествено. Така всяко число с умножение може да се сведе до това уравнение:
- 25×3 = 75
- 25 + 25 + 25 = 75
- 25×3 = 25 + 25 + 25
От това уравнение следва, че че умножението е опростено събиране.
Какво е нула
 Всеки знае от детството: нулата е празнота, въпреки че тази празнота има обозначение, тя не носи нищо. Древните източни учени са мислили по друг начин - те са подходили към въпроса философски и са направили някои паралели между празнотата и безкрайността и са видели дълбок смисълв това число. В края на краищата нула, което има значението на празнота, стояща до всяко естествено число, го умножава десетократно. Оттук и всички спорове относно умножението - това число носи толкова много непоследователност, че става трудно да не се объркате. В допълнение, нулата се използва постоянно за определяне на празни цифри в десетични дроби, това се прави както преди, така и след десетичната точка.
Всеки знае от детството: нулата е празнота, въпреки че тази празнота има обозначение, тя не носи нищо. Древните източни учени са мислили по друг начин - те са подходили към въпроса философски и са направили някои паралели между празнотата и безкрайността и са видели дълбок смисълв това число. В края на краищата нула, което има значението на празнота, стояща до всяко естествено число, го умножава десетократно. Оттук и всички спорове относно умножението - това число носи толкова много непоследователност, че става трудно да не се объркате. В допълнение, нулата се използва постоянно за определяне на празни цифри в десетични дроби, това се прави както преди, така и след десетичната точка.
Възможно ли е да се умножава по празнота?
Възможно е да се умножи по нула, но е безполезно, защото, каквото и да се каже, дори когато се умножава отрицателни числапак ще е нула. Достатъчно е просто да запомните това просто правило и никога повече да не задавате този въпрос. Всъщност всичко е по-просто, отколкото изглежда на пръв поглед. Няма скрити значения и тайни, както вярваха древните учени. По-долу ще дадем най-логичното обяснение, че това умножение е безполезно, защото когато умножите число по него, пак ще получите същото - нула.
Връщайки се в самото начало, към аргумента за две ябълки, 2 по 0 изглежда така:
- Ако изядете две ябълки пет пъти, тогава ще изядете 2×5 = 2+2+2+2+2 = 10 ябълки
- Ако изядете две от тях три пъти, тогава ще изядете 2×3 = 2+2+2 = 6 ябълки
- Ако изядете две ябълки нула пъти, тогава нищо няма да бъде изядено - 2×0 = 0×2 = 0+0 = 0
В крайна сметка да ядете ябълка 0 пъти означава да не ядете нито една. Ще стане ясно дори на вас самите на малко дете. Каквото и да се каже, резултатът ще бъде 0, две или три могат да бъдат заменени с абсолютно всяко число и резултатът ще бъде абсолютно същият. И казано просто, тогава нулата е нищо, и кога имате няма нищо, тогава колкото и да умножавате, пак е същото ще бъде нула. Няма такова нещо като магия и нищо няма да направи ябълка, дори ако умножите 0 по милион. Това е най-простото, разбираемо и логично обяснение на правилото за умножение по нула. За човек, който е далеч от всички формули и математика, такова обяснение ще бъде достатъчно, за да разреши дисонанса в главата и всичко да си дойде на мястото.
дивизия
От всичко по-горе следва още едно важно правило:
Не можеш да делиш на нула!
 Това правило също упорито ни се набива в главите от детството. Просто знаем, че е невъзможно да направим всичко, без да пълним главите си с ненужна информация. Ако неочаквано ви зададат въпроса защо е забранено да се дели на нула, тогава повечето ще бъдат объркани и няма да могат да отговорят ясно на най-простия въпрос от училищната програма, тъй като няма толкова много спорове и противоречия около това правило.
Това правило също упорито ни се набива в главите от детството. Просто знаем, че е невъзможно да направим всичко, без да пълним главите си с ненужна информация. Ако неочаквано ви зададат въпроса защо е забранено да се дели на нула, тогава повечето ще бъдат объркани и няма да могат да отговорят ясно на най-простия въпрос от училищната програма, тъй като няма толкова много спорове и противоречия около това правило.
Всички просто запомниха правилото и не разделиха на нула, без да подозират, че отговорът е скрит на повърхността. Събирането, умножението, делението и изваждането са неравностойни; от горните са валидни само умножението и събирането, а всички други манипулации с числа са изградени от тях. Тоест нотацията 10: 2 е съкращение на уравнението 2 * x = 10. Това означава, че нотацията 10: 0 е същото съкращение за 0 * x = 10. Оказва се, че деленето на нула е задача за намерете число, умножавайки по 0, получавате 10 И вече разбрахме, че такова число не съществува, което означава, че това уравнение няма решение и ще бъде априори неправилно.
Нека ви кажа,
За да не се дели на 0!
Нарежете 1, както искате, по дължина,
Само не дели на 0!
Самата нула е много интересно число. Само по себе си означава празнота, липса на смисъл, а до друго число увеличава значението си 10 пъти. Всички числа на нулева степен винаги дават 1. Този знак е бил използван в цивилизацията на маите и е обозначавал също понятието „начало, причина“. Дори календарът започваше с нулев ден. Тази цифра също е свързана със строга забрана.
От началото ученически годиниВсички сме научили ясно правилото „не можете да делите на нула“. Но ако в детството приемате много неща на вяра и думите на възрастен рядко предизвикват съмнения, тогава с течение на времето понякога все още искате да разберете причините, да разберете защо са установени определени правила.
Защо не можете да разделите на нула? Бих искал да получа ясно логично обяснение на този въпрос. В първи клас учителите не можеха да направят това, защото в математиката правилата се обясняват с уравнения, а на тази възраст нямахме представа какво е това. И сега е време да го разберете и да получите ясно логично обяснение защо не можете да делите на нула.
Факт е, че в математиката само две от четирите основни операции (+, -, x, /) с числа се признават за независими: умножение и събиране. Останалите операции се считат за производни. Нека да разгледаме един прост пример.

Кажете ми колко ще получите, ако извадите 18 от 20? Естествено, в главата ни веднага изниква отговорът: ще бъде 2. Как стигнахме до този резултат? Този въпрос ще изглежда странен за някои - в крайна сметка всичко е ясно, че резултатът ще бъде 2, някой ще обясни, че е взел 18 от 20 копейки и е получил две копейки. Логично всички тези отговори не подлежат на съмнение, но от математическа гледна точка този проблем трябва да бъде решен по различен начин. Нека припомним още веднъж, че основните операции в математиката са умножение и събиране и затова в нашия случай отговорът се крие в решаването на следното уравнение: x + 18 = 20. От което следва, че x = 20 - 18, x = 2 . Изглежда защо да описваме всичко толкова подробно? В крайна сметка всичко е толкова просто. Без това обаче е трудно да се обясни защо не можете да разделите на нула.
Сега да видим какво се случва, ако искаме да разделим 18 на нула. Нека създадем уравнението отново: 18: 0 = x. Тъй като операцията деление е производна на процедурата за умножение, трансформирайки нашето уравнение, получаваме x * 0 = 18. Тук започва задънената улица. Всяко число вместо X, когато се умножи по нула, ще даде 0 и няма да можем да получим 18. Сега става пределно ясно защо не можете да делите на нула. Самата нула може да бъде разделена на произволно число, но обратното - уви, това е невъзможно.
Какво се случва, ако разделите нулата сама по себе си? Това може да се запише по следния начин: 0: 0 = x или x * 0 = 0. Това уравнение има безкраен брой решения. Следователно крайният резултат е безкрайност. Следователно операцията в този случай също няма смисъл.

Деленето на 0 е в основата на много въображаеми математически шеги, които могат да бъдат използвани, за да озадачат всеки невеж човек, ако желае. Например, разгледайте уравнението: 4*x - 20 = 7*x - 35. Нека извадим 4 от скобите от лявата страна и 7 отдясно. Получаваме: 4*(x - 5) = 7*(x - 5). Сега нека умножим лявата и дясната страна на уравнението по дробта 1 / (x - 5). Уравнението ще приеме следната форма: 4*(x - 5)/(x - 5) = 7*(x - 5)/ (x - 5). Нека намалим дробите с (x - 5) и се оказва, че 4 = 7. От това можем да заключим, че 2*2 = 7! Разбира се, уловката тук е, че е равно на 5 и беше невъзможно да се съкратят дроби, тъй като това доведе до деление на нула. Ето защо, когато редуцирате дроби, винаги трябва да проверявате дали нула случайно не попада в знаменателя, в противен случай резултатът ще бъде напълно непредвидим.
Евгений ШИРЯЕВ, преподавател и ръководител на лабораторията по математика на Политехническия музей, каза на AiF за деленето на нула:
1. Компетентност на въпроса
Съгласете се, това, което прави правилото особено провокативно, е забраната. Как да не стане това? Кой забрани? Ами нашите граждански права?
Нито Конституцията, нито Наказателният кодекс, нито дори уставът на вашето училище възразява срещу интелектуалното действие, което ни интересува. Това означава, че забраната няма правна сила и нищо не ви пречи да се опитате да разделите нещо на нула точно тук, на страниците на AiF. Например хиляда.
2. Да разделим, както ни учи
Спомнете си, когато за първи път научихте как да делите, първите примери бяха решени с проверка на умножението: резултатът, умножен по делителя, трябваше да съвпада с делителя. Не съвпадна - те не решиха.
Пример 1. 1000: 0 =...
Нека за момент забравим за забраненото правило и направим няколко опита да познаем отговора.
Неправилните ще бъдат отрязани от проверката. Опитайте следните опции: 100, 1, −23, 17, 0, 10 000 За всяка от тях проверката ще даде същия резултат:
100 0 = 1 0 = − 23 0 = 17 0 = 0 0 = 10 000 0 = 0
Чрез умножаване на нула всичко се превръща в себе си и никога в хиляда. Изводът е лесен за формулиране: нито едно число няма да премине теста. Тоест нито едно число не може да бъде резултат от разделяне на ненулево число на нула. Такова разделение не е забранено, но просто няма резултат.
3. Нюанс
Почти пропуснахме една възможност да опровергаем забраната. Да, признаваме, че ненулево число не може да бъде разделено на 0. Но може би самата 0 може?
Пример 2. 0: 0 = ...
Какви са вашите предложения за лично? 100? Моля: частното от 100, умножено по делителя 0, е равно на дивидент 0.
Повече опций! 1? Става също. И −23, и 17, и това е. В този пример тестът ще бъде положителен за всяко число. И, честно казано, решението в този пример трябва да се нарича не число, а набор от числа. Всеки. И не отнема много време, за да се съгласим, че Алис не е Алис, а Мери Ан и двете са мечта на заек.
4. Ами висшата математика?
Проблемът е решен, нюансите са взети предвид, точките са поставени, всичко е ясно - отговорът на примера с деление на нула не може да бъде едно число. Решаването на подобни проблеми е безнадеждно и невъзможно. Което означава... интересно! Вземи две.
Пример 3. Разберете как да разделите 1000 на 0.
Но няма начин. Но 1000 може лесно да се раздели на други числа. Е, нека поне да направим това, което работи, дори и да променим задачата. И тогава, разбирате ли, ние се увличаме и отговорът ще се появи сам. Нека забравим за нулата за минута и да разделим на сто:
Сто е далеч от нула. Нека направим крачка към него, като намалим делителя:
1000: 25 = 40,
1000: 20 = 50,
1000: 10 = 100,
1000: 8 = 125,
1000: 5 = 200,
1000: 4 = 250,
1000: 2 = 500,
1000: 1 = 1000.
Очевидна динамика: колкото по-близо до нула е делителя, толкова по-голямо е частното. Тенденцията може да се наблюдава допълнително, като преминете към дроби и продължите да намалявате числителя:
Остава да отбележим, че можем да се доближим до нулата колкото си искаме, правейки коефициента толкова голям, колкото желаем.
В този процес няма нула и няма последно частно. Ние посочихме движението към тях, като заменихме числото с последователност, сближаваща се с числото, което ни интересува:
Това предполага подобна замяна на дивидента:
1000 ↔ { 1000, 1000, 1000,... }
Не е за нищо, че стрелките са двустранни: някои последователности могат да се сближат с числа. След това можем да свържем последователността с числовата й граница.
Нека да разгледаме последователността от частни:
Той расте неограничено, без да се стреми към никакво число и да надминава нито едно. Математиците добавят символи към числата ∞, за да можете да поставите двустранна стрелка до такава последователност:
Сравнението с броя на последователностите, които имат ограничение, ни позволява да предложим решение на третия пример:
Когато поелементно разделим последователност, сходяща се към 1000, на последователност от положителни числа, сближаваща се с 0, получаваме последователност, сходяща се към ∞.
5. И тук е нюансът с две нули
Какъв е резултатът от разделянето на две поредици от положителни числа, които се събират към нула? Ако те са еднакви, тогава единицата е идентична. Ако последователност от дивиденти се сближава към нула по-бързо, тогава по-специално това е последователност с нулева граница. И когато елементите на делителя намаляват много по-бързо от тези на дивидента, последователността на частното ще нарасне значително:
Несигурна ситуация. И това се нарича: несигурност на типа 0/0 . Когато математиците видят последователности, които отговарят на такава несигурност, те не бързат да разделят двете еднакви числаедин срещу друг, но разберете коя от последователностите работи по-бързо до нула и как точно. И всеки пример ще има свой конкретен отговор!
6. В живота
Законът на Ом свързва тока, напрежението и съпротивлението във верига. Често се пише в следната форма:
Нека си позволим да пренебрегнем чистото физическо разбиране и формално да разгледаме дясната страна като частно на две числа. Нека си представим, че решаваме училищна задача за електричество. Условието дава напрежението във волтове и съпротивлението в омове. Въпросът е очевиден, решението е в едно действие.
Сега нека разгледаме определението за свръхпроводимост: това е свойството на някои метали да имат нулево електрическо съпротивление.
Добре, нека решим задачата за свръхпроводяща верига? Просто го настройте така R= 0 Ако не се получи, физиката изхвърля интересен проблем, зад който очевидно стои научно откритие. И хората, които успяха да разделят на нула в тази ситуация, получиха Нобелова награда. Полезно е да можете да заобикаляте всякакви забрани!
Строга забрана за деление на нула се налага дори в по-ниските класове на училище. Децата обикновено не се замислят за причините за това, но всъщност да знаят защо нещо е забранено е едновременно интересно и полезно.
Аритметични операции
Аритметичните действия, които се изучават в училище, не са еквивалентни от гледна точка на математиците. Те признават за валидни само две от тези операции – събиране и умножение. Те са включени в самото понятие число и всички други действия с числата по един или друг начин са изградени върху тези две. Тоест, не само деленето на нула е невъзможно, но делението изобщо е невъзможно.
Изваждане и деление
Какво липсва на останалите действия? Отново знаем от училище, че например изваждането на четири от седем означава да вземете седем сладки, да изядете четири от тях и да преброите останалите. Но математиците, когато ядат сладкиши и изобщо, ги възприемат съвсем различно. За тях има само събиране, тоест записът 7 - 4 означава число, което, когато се добави към числото 4, ще бъде равно на 7. Тоест за математиците 7 - 4 е кратък запис на уравнението : x + 4 = 7. Това не е изваждане, а задача - намерете числото, което трябва да се постави на мястото на x.
Същото важи и за деленето и умножението. Разделяйки десет на две, младши ученик поставя десет бонбона в две еднакви купчини. Математикът вижда уравнението и тук: 2 x = 10.

Това обяснява защо деленето на нула е забранено: то е просто невъзможно. Записът 6: 0 трябва да се превърне в уравнението 0 · x = 6. Тоест трябва да намерите число, което може да се умножи по нула и да получите 6. Но е известно, че умножението по нула винаги дава нула. Това е основното свойство на нулата.
Следователно няма число, което, когато се умножи по нула, би дало някакво число, различно от нула. Това означава, че това уравнение няма решение, няма число, което да корелира с нотацията 6: 0, тоест няма смисъл. Те говорят за неговата безсмисленост, когато делението на нула е забранено.
Нулата дели ли се на нула?
Възможно ли е да се раздели нула на нула? Уравнението 0 · x = 0 не създава никакви затруднения и можете да вземете тази нула за x и да получите 0 · 0 = 0. Тогава 0: 0 = 0? Но ако, например, вземем едно като x, получаваме също 0 1 = 0. Можете да вземете произволно число за x и да го разделите на нула и резултатът ще остане същият: 0: 0 = 9, 0 : 0 = 51 и така нататък.

По този начин в това уравнение може да се вмъкне абсолютно всяко число и е невъзможно да се избере конкретно, невъзможно е да се определи кое число се обозначава с нотацията 0: 0. Тоест тази нотация също няма смисъл и разделянето с нула все още е невъзможно: дори не се дели на себе си.
Това е важна характеристика на операцията деление, тоест умножението и свързаното число нула.
Остава въпросът: възможно ли е да го извадим? Можем да кажем, че истинската математика започва с това интересен въпрос. За да намерите отговора на него, трябва да научите формалните математически дефиниции на наборите от числа и да се запознаете с операциите върху тях. Например, има не само прости, но и чието разделяне се различава от разделянето на обикновените. Това не е включено в училищна програма, но лекциите по математика в университета започват именно с това.
клас: 3
учебник:„Математика“ от M.I
Цели на урока:създават условия за развиване на способността да се дели 0 на число.
Цели на урока:
- разкриват смисъла на деленето на 0 с число чрез връзката между умножение и деление;
- развиват независимост, внимание, мислене;
- развиват умения за решаване на примери за таблично умножение и деление.
За постигане на целта урокът е проектиран, като се вземат предвид дейностен подход.
Структурата на урока включва:
- орг. момент, чиято цел бе положително мотивиране на децата за учене.
- Мотивацияни позволи да актуализираме знанията, да формулираме целите и задачите на урока. За целта бяха предложени задачи за намиране на допълнително число, класифициране на примери в групи, добавяне на липсващи числа. При решаването на тези задачи децата се сблъскаха с проблем: намерен е пример, за чието решаване съществуващите знания не са достатъчни. В тази връзка децата независимо формулира цели си поставят учебните цели на урока.
- Търсене и откриване на нови знаниядаде възможност на децата предлагат различни опциирешения на задачи. Въз основа на предварително проучен материал,успяха да намерят правилното решение и да стигнат до заключение, в който е формулирано ново правило.
- По време на първична консолидациястуденти коментиравашите действия, работейки по правилото, бяха допълнително избрани вашите примерикъм това правило.
- За автоматизация на действиятаИ способност за използване на правила в нестандартниВ задачите децата решаваха уравнения и изрази в няколко стъпки.
- Самостоятелна работа и извършено взаимна проверкапоказа, че повечето деца разбират темата.
- По време на отраженияДецата заключиха, че целта на урока е постигната и се оцениха с помощта на картите.
Урокът се основаваше на независими действия на учениците на всеки етап, пълно потапяне в учебна задача. Това беше улеснено от такива техники като работа в групи, само- и взаимно тестване, създаване на ситуация на успех, диференцирани задачи, саморефлексия.
По време на часовете
| Предназначение на сцената | Съдържание на сцената | Студентска дейност | ||||||||||||
| 1. Орг. момент | ||||||||||||||
| Подготовка на учениците за работа, положително отношение към учебните дейности. | Стимули за образователна дейност. Проверете готовността си за урока, седнете изправени, облегнете се на облегалката на стола. Разтрийте ушите си, така че кръвта да тече по-активно към мозъка. Днес ще имате много интересна работа, която съм сигурен, че ще се справите много добре. |
Организация на работното място, проверка на годността. | ||||||||||||
| 2. Мотивация. | ||||||||||||||
| Стимулиране на когнитивните дейност, активиране на мисловния процес |
Актуализиране на знанията, достатъчни за придобиване на нови знания. Устно броене. Проверка на знанията ви за таблично умножение: |
Решаване на задачи, базирани на знания за таблично умножение. | ||||||||||||
| А) намерете допълнителното число: 2 4 6 7 10 12 14 6 18 24 29 36 42 Обяснете защо е излишен и какъв номер трябва да се използва за заместването му. |
Намиране на допълнителното число. | |||||||||||||
| Б) въведете липсващите числа: … 16 24 32 … 48 … |
Добавяне на липсващото число. | |||||||||||||
| Създаване на проблемна ситуация Задачи по двойки: В) подредете примерите в 2 групи: Защо се разпространи по този начин? (с отговор 4 и 5). |
Класифициране на примери в групи. | |||||||||||||
| Карти: 8·7-6+30:6= 28:(16:4) 6= 30-(20-10:2):5= 30-(20-10 2):5= |
Силните ученици работят върху индивидуални карти. | |||||||||||||
| Какво забелязахте? Има ли друг пример тук? Успяхте ли да решите всички примери? Кой има проблеми? С какво този пример е по-различен от останалите? Ако някой е решил браво. Но защо не всички можеха да се справят с този пример? |
Откриване на проблема. Идентифициране на липсващи знания и причини за затруднения. |
|||||||||||||
| Поставяне на учебна задача. Ето пример с 0. А от 0 можете да очаквате различни трикове. Това е необичайно число. Спомнете си какво знаете за 0? (a 0=0, 0 a=0, 0+a=a) Дай примери. Вижте колко е коварно: когато се събира, не променя числото, но когато се умножи, го превръща в 0. Тези правила важат ли за нашия пример? Как ще се държи при хранене? |
Наблюдение на известни техники за работа с 0 и корелация с оригиналния пример. | |||||||||||||
| И така, каква е нашата цел? Решете правилно този пример. Таблица на дъската. Какво е необходимо за това? Научете правилото за деление на 0 на число. |
Предлагане на хипотеза | |||||||||||||
| Как да намерим правилното решение? Какво действие включва умножението? (с разделяне) Дай пример 2 3 = 6 6: 2 = 3 Може ли сега 0:5? Това означава, че трябва да намерите число, което, умножено по 5, е равно на 0. х 5=0 Това число е 0. Така че 0:5=0. Дайте свои собствени примери. |
търсене на решение въз основа на това, което е било проучено преди това, | |||||||||||||
| Формулиране на правилото. Какво правило може да се формулира сега? Когато разделите 0 на число, получавате 0. 0: а = 0. |
Решение типични задачис коментар. Работете по схемата (0:a=0) |
|||||||||||||
| 5. Физически упражнения. | ||||||||||||||
| Предотвратяване на лоша стойка, облекчаване на умората на очите, общата умора. | ||||||||||||||
| 6. Автоматизация на знанията. | ||||||||||||||
| Идентифициране на границите на приложимост на новите знания. | Какви други задачи може да изискват познаване на това правило? (при решаване на примери, уравнения) |
Използване на придобитите знания в различни задачи. Работа в групи. |
||||||||||||
| Какво е неизвестното в тези уравнения? Спомнете си как да намерите неизвестен множител. Решете уравненията. Какво е решението на уравнение 1? (0) На 2? (няма решение, не може да се дели на 0) |
Припомняне на предишни умения. | |||||||||||||
| ** Създайте уравнение с решението x=0 (x 5=0) | За силни ученици творческа задача | |||||||||||||
| 7. Самостоятелна работа. | ||||||||||||||
| Развитие на независимост и когнитивни способности | Самостоятелна работа, последвана от взаимна проверка. №6 |
Активни умствени действия на учениците, свързани с търсене на решения въз основа на техните знания. Самоконтрол и взаимен контрол. Силните ученици проверяват и помагат на по-слабите. |
||||||||||||
| 8. Работа върху вече преминат материал. Упражняване на умения за решаване на проблеми. | ||||||||||||||
| Формиране на умения за решаване на проблеми. | Смятате ли, че числото 0 често се използва в задачи? (Не, не често, защото 0 е нищо и задачите трябва да съдържат някакво количество от нещо.) След това ще решаваме задачи, в които има други числа. Прочетете проблема. Какво ще помогне за решаването на проблема? (таблица) Кои колони в таблицата трябва да бъдат записани? Попълнете таблицата. Направете план за решение: какво трябва да се научи в стъпки 1 и 2? |
Работа върху проблем с помощта на таблица. Планиране за решаване на проблем. Самозаписване на решението. Самоконтрол по модел. |
||||||||||||
| 9. Рефлексия. Обобщение на урока. | ||||||||||||||
| Организация на самооценка на дейностите. Повишаване на мотивацията на детето. |
По каква тема работихте днес? Какво не знаехте в началото на урока? Каква цел си поставихте? Постигнахте ли го? На какво правило попаднахте? Оценете работата си, като поставите отметка на съответната икона:
| Осъзнаване на вашите дейности, самоанализ на вашата работа. Записване на съответствието на резултатите от изпълнението и поставената цел. | ||||||||||||
| 10. Домашна работа. | ||||||||||||||