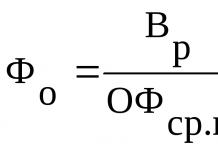Nedávno sa tu objavila téma plánovania tried a chcel som sa porozprávať o mojich skúsenostiach s vytváraním plánovacieho algoritmu pre univerzitu, alebo skôr o heuristike, ktorú som použil.

Nie je to tak dávno, v roku 2002, keď som končil univerzitu (jaroslavlská pobočka MESI), odbor „Aplikovaná informatika v ekonómii“, stál som pred úlohou vybrať si prácu. Navrhovaný zoznam tém bol deprimujúci, väčšinou nudný vývoj databázy. V zásade by som mohol vziať za základ niektoré z mojich existujúcich vývojov, ako navrhol vedúci. oddelenie, no vrela mi krv, chcela som pre seba urobiť niečo zaujímavé a nové. Manažérovi som navrhol tému rozvrhovania, najmä preto, že som pracoval v IT službe na vysokej škole a mal som na starosti systém KIS UZ (Integrovaný informačný systém pre riadenie vzdelávacích inštitúcií), produkt Jaroslavľskej spoločnosti. KIS UZ bola dobrá, ale sama si nedokázala vytvoriť rozvrh. Aj týmto som išiel za cieľom urobiť niečo užitočné, no ukázalo sa, že pokusy o realizáciu neboli, možno niekomu aspoň zverejnenie na Habré prospeje.

Bolo teda potrebné naučiť počítač vytvárať týždenný rozvrh hodín, a to čo najlepšie. Uvedomujúc si rozsah vyhľadávacieho priestoru, nestanovil som si za cieľ nájsť najlepšiu možnosť. Najprv musíte určiť, čo sú triedy a čo je dobré a čo zlé. Bol vybraný nasledujúci model, ktorý má nasledujúce vstupné údaje:
- počet dní v týždni
- počet tried za deň
- zoznam učiteľov
- zoznam skupín, podskupín a vlákien
- počet divákov podľa konkrétneho typu
- súbor skupín úloh (činností):

• trieda
• učiteľ
• stream alebo skupina
• typ publika
• počet tried v tejto skupine tried
• čas, ak chce riaditeľ túto činnosť „pevne“ nastaviť na určitý čas

Proces by mal usporiadať triedy na časovej mriežke - rozvrhu. Pri vyhodnocovaní rozvrhu sa podieľajú 4 parametre - počet „okien“ v rozvrhu skupiny a učiteľov, rovnomerné rozloženie hodín počas dní pre skupinu a učiteľov. Význam týchto parametrov nastavuje riaditeľ. Najprv som chcel použiť metódu analýzy hierarchií v objektívnej funkcii, ale musel by som zaviesť párové porovnanie týchto parametrov, tak som si vystačil s lineárnou funkciou.

Čo sa týka učební, tak som to zjednodušil, vyškrtol z rozvrhu, čím sa obmedzil, pri hľadaní sa bral do úvahy počet voľných učební v konkrétnom čase. Po vygenerovaní harmonogramu v čase boli audiencie usporiadané. Vo všeobecnosti ide o jednoduchý model, ktorý som načrtol. Trochu som experimentoval s genetickým algoritmom, počas dňa som načrtol program založený na knižnici, ale výsledok sa mi nepáčil a bez rozmýšľania som prešiel na iné algoritmy. Myslím si, že zlý výsledok bol spôsobený mojím neopodstatneným prístupom, s najväčšou pravdepodobnosťou som neúspešne kódoval model z hľadiska GA. Začal som uvažovať o metóde vetvy a väzby. Vyhľadávací priestor je strom, kde úroveň predstavuje obsadenie a vetva predstavuje prvok časovej mriežky. Plán sa považuje za cestu od koreňa stromu k jednému z visiacich vrcholov. Počas procesu vetvenia sa kontroluje možnosť a uskutočniteľnosť obchvatu podľa rôznych kritérií: zaneprázdnenosť učiteľa, skupiny, hodnotenie. Obchádzanie stromu, prirodzene, do hĺbky. Na každej úrovni sú voľné bunky mriežky pre aktuálnu úlohu. Ak má riaditeľ „pevne“ pridelenú danú úlohu na určitý čas, potom je vybudovaná jedna vetva zodpovedajúca určitému času. Ďalej, prechádzajúc pozdĺž vetvy, sa nájde odhad hornej hranice (plus sa vykonáva kontrola prítomnosti voľného publika tohto typu) a ak je odhad hornej hranice vyšší ako odhad najlepšieho rozvrhu momentálne nájdené (a ak existuje voľné publikum tohto typu), potom prechádzame cez pobočky, inak prejdeme na ďalšiu vetvu. V metóde vetvenia a hraníc je kľúčovým a dôležitým bodom algoritmus na nájdenie odhadu hornej hranice. Bez ďalších okolkov som posúdil aktuálny neúplný rozvrh a porovnal som ho s aktuálnym najlepším nájdeným rozvrhom. Keďže ideme ďalej, odhad neúplného rozvrhu sa zhorší, potom ak je už horší ako odhad najlepšieho rozvrhu, vetva sa zamietne. A tak keď som to celé naprogramoval, pripravil dáta (prebral som ich zo systému na základe reálnych dát), večer som to spustil a išiel domov. Ráno, keď som prišiel do práce, som do UZ CIS nahral to najlepšie z miliardy nájdených rozpisov, no bez sĺz sa na to nedalo pozerať. Bola som sklamaná, skľúčená a nevedela som ako ďalej. Večer som išiel s kamarátmi na pivo a teraz stojím na zastávke opitý a čakám na poslednú električku a v hlave sú len stromy, konáre, medze, odhady... a potom svitá. na každej úrovni, pri určovaní vetiev, ich triediť, uistiť sa, že tie možnosti sú na prvom mieste, u ktorých je väčšia pravdepodobnosť, že budú súčasťou najlepšieho rozvrhu ako iné. Ale ako to urobiť? Tá myšlienka prišla, keď som už dofajčil druhú cigaretu. Najprv je potrebné zostaviť si vlastné ideálne rozvrhy pre každý predmet rozvrhu a pre každý odbor vypočítať mieru zaradenia do týchto rozvrhov a zoradiť podľa neho. Ráno som kráčal do práce rýchlejšie ako zvyčajne, cestou som si v hlave kreslil technické detaily, do obeda bola heuristika zabudovaná, výsledok vyzeral v UZ CIS celkom slušne a zvyšnú polovicu pracovného dňa som sa usmieval .

PS. Neskôr, keď som počul o PageRank, myslel som si, že má niečo podobné ako táto heuristika.

Väčšina z toho, čo tu čítate, sú nezmysly. Na niektorých miestach však podľa môjho názoru existujú myšlienky zdravého rozumu, žiaľ, nie je takých miest až tak veľa. L Nech vás ani nenapadne brať to tam, kde sa vážne študujú problémy teórie plánovania. Každému, kto chce napísať niečo lepšie ako toto, vrelo odporúčam prečítať si Huovu knihu. T. „Celočíselné programovanie a toky v sieťach“, okrem toho sa pravdepodobne oplatí prečítať si prednášky VMiK o teórii optimalizácie od N.M. Novikova (nepamätám si, kde je to na internete). Teraz aktívne pracujem na problémoch teórie optimalizácie, takže každý, koho táto téma tiež zaujíma, sa vždy rád porozpráva. Napíšte [chránený e-mailom].

Úvod. 8

1. Popis technologickej oblasti. 10

1.1. Formulácia problému plánovania. 10

1.1.1. Všeobecná formulácia problému plánovania. 10

1.1.2. Formulácia úlohy zostavenia rozvrhu aplikovaného na rozvrh tréningov. jedenásť

1.2. Analýza existujúceho softvéru... 12

1.3. Formulácia problému. 15

2. Vývoj matematického modelu a praktická implementácia automatického plánovacieho systému. 16

2.1. Matematický model rozvrhu na vysokej škole. 16

2.1.1. Notový zápis. 16

2.1.2. Premenné. 18

2.1.3. Obmedzenia. 19

2.1.4. Cieľová funkcia. 21

2.2. Metódy riešenia problému. 22

2.2.1. Plne celočíselný algoritmus. 23

2.2.2 Algoritmus priameho celočíselného programovania. 28

2.2.3. Technika na získanie počiatočného prípustného základu. 32

2.3. Vlastnosti praktickej implementácie systému.. 36

2.3.1. Výber modelu. 36

2.3.2. Popis vstupných informácií. 39

2.3.3. Rozvoj informačnej podpory úlohy. 41

2.3.4. Vlastnosti tvorby obmedzení v matematickom modeli problému plánovania. 44

2.4. Výsledky programu.. 45

2.5. Analýza získaných výsledkov. 49

Závery... 50

Literatúra. 51

Dodatok 1. Možnosti softvérových produktov pre plánovacie systémy. 52

Príloha 2. Výpis softvérového modulu metód na riešenie problému automatického plánovania. 61

Úvod

Kvalita prípravy odborníkov na vysokých školách a najmä efektívnosť využívania vedeckého a pedagogického potenciálu do určitej miery závisia od úrovne organizácie vzdelávacieho procesu.

Jedna z hlavných súčastí tohto procesu - rozvrh hodín - reguluje pracovný rytmus a ovplyvňuje tvorivý výkon učiteľov, preto ho možno považovať za faktor optimalizácie využívania obmedzených pracovných zdrojov - pedagogických zamestnancov. Technológiu na vypracovanie harmonogramu treba vnímať nielen ako pracne náročný technický proces, predmet mechanizácie a automatizácie pomocou počítača, ale aj ako činnosť optimálneho riadenia. Toto je teda problém rozvoja optimálnych rozvrhov tried na univerzitách so zjavnými ekonomickými výhodami. Keďže záujmy účastníkov vzdelávacieho procesu sú rôznorodé, úloha tvorby harmonogramu je multikriteriálna.

Úlohu tvorby rozvrhu nemožno chápať len ako druh programu, ktorý vykonáva funkciu mechanického rozdeľovania tried na začiatku semestra, v ktorom sa končí jeho (programové) používanie. Ekonomický efekt z efektívnejšieho využívania pracovných zdrojov možno dosiahnuť len ako výsledok usilovnej práce pri riadení týchto pracovných zdrojov. Harmonogram je tu len nástrojom takéhoto riadenia a pre jeho plnohodnotné využitie je potrebné, aby program spájal nielen prostriedky na vytvorenie optimálneho harmonogramu, ale aj prostriedky na udržanie jeho optimality v prípade zmeny niektorých vstupných údajov, ktoré sa v čase zostavovania harmonogramu považovali za konštantné . Navyše, optimálne riadenie takého komplexného systému nie je možné bez nahromadenia niektorých štatistických informácií o procesoch prebiehajúcich v systéme. Preto samotná úloha vytvorenia optimálneho rozvrhu je len súčasťou komplexného systému riadenia vzdelávacieho procesu.

Multikriteriálna povaha tohto problému a zložitosť objektu, pre ktorý je matematický model zostavený, si vyžaduje serióznu matematickú štúdiu objektu, aby sa zvýšila funkčnosť plánovacích algoritmov bez toho, aby sa výrazne skomplikoval model a v dôsledku toho sa zvýšil počet použitej pamäte a času potrebného na vyriešenie problému.

1. POPIS TECHNOLOGICKEJ OBLASTI 1.1. Formulácia problému plánovania

Problém teórie plánovania vo svojej všeobecnej formulácii sa považuje za veľmi atraktívny, hoci dosiahnutie čo i len malého pokroku k riešeniu je zvyčajne spojené s obrovskými ťažkosťami. Napriek tomu, že problematikou teórie plánovania sa zaoberalo mnoho vysokokvalifikovaných odborníkov, doteraz sa nikomu nepodarilo získať žiadne významné výsledky. Neúspešné pokusy o získanie takýchto výsledkov sa spravidla nezverejňujú, čo je čiastočne spôsobené tým, že tento problém naďalej priťahuje pozornosť mnohých výskumníkov kvôli zjavnej jednoduchosti formulácie.

1.1.1. Všeobecná formulácia problému plánovania

Vo svojej najvšeobecnejšej formulácii je úloha plánovania nasledovná. Pomocou určitého súboru zdrojov alebo obslužných zariadení je potrebné vykonávať určitý pevný systém úloh. Cieľom je nájsť efektívny algoritmus na objednávanie úloh, ktorý optimalizuje alebo má tendenciu optimalizovať požadovanú mieru efektívnosti vzhľadom na vlastnosti úloh a zdrojov a na ne kladené obmedzenia. Hlavnými mierami efektívnosti sú dĺžka rozvrhu a priemerný čas zotrvania pracovných miest v systéme. Modely týchto problémov sú deterministické v tom zmysle, že všetky informácie, na základe ktorých sa prijímajú rozhodnutia o usporiadaní, sú vopred známe.

1.1.2. Formulácia úlohy zostavenia rozvrhu aplikovaného na rozvrh tréningov.

Všeobecná teória plánovania predpokladá, že všetky obslužné zariadenia (alebo procesory) nemôžu vykonávať viac ako jednu úlohu v danom čase, čo nestačí na plánovanie vzdelávacích hodín, ak sa trieda berie ako procesor pri rozdeľovaní úloh. Takže v niektorých prípadoch sa triedy s viacerými skupinami súčasne môžu konať v jednej triede, napríklad všeobecné prednášky pre niekoľko prúdov.

Preto pri prenose všeobecnej teórie rozvrhov do rozvrhu školení boli prijaté tieto predpoklady:

Všetky procesory (t.j. v prípade rozvrhu vzdelávania - učebne) majú kapacitu - určitý počet C ≥ 1. Kapacita procesora určuje počet úloh, ktoré môže súčasne „spracovať“ v danom čase (s vzhľadom na nejednotnosť spracovateľov by bolo zaujímavé zvážiť možnosť , keď spracovateľom nie je publikum, ale učiteľ a úlohou je prúd z jednej alebo viacerých vzdelávacích skupín, s ktorými pracuje);

Súbor úloh na rozdelenie zahŕňa školenia učiteľov so študijnými skupinami;

Časový model v systéme je diskrétny; predpokladá sa, že celé rozdelenie sa periodicky opakuje v určitom časovom intervale;

Všetky úlohy sú splnené v rovnakom čase, ktorý sa berie ako jednotka diskretizácie časového intervalu;

Zadania patria k objektom, ktorými sú študijné skupiny a učitelia.

V dôsledku toho je formulácia problému plánovania školení nasledovná: „Pre daný súbor učební (v tomto prípade učebňa znamená širokú škálu miestností, v ktorých sa školenia konajú (od počítačovej učebne po telocvičňa)) a daný súbor časových intervalov (t. j. v podstate lekcie alebo tréningové dvojice) na zostavenie takého rozdelenia tréningov pre všetky objekty (učiteľov a tréningové skupiny), pre ktoré je zvolené kritérium optimality najlepšie."

1.2. Analýza existujúceho softvéru

V súčasnosti je sektor softvérového trhu pre systémy plánovania tried zastúpený veľkým počtom rôznych softvérových produktov. Tabuľka 1 zobrazuje len niektoré z tých, ktoré sú mi známe.

Z objektívnych dôvodov musí plánovací systém na univerzite (rozumej veľkej štátnej univerzite) nevyhnutne implementovať niekoľko základných funkcií:

Berúc do úvahy želania učiteľov;

Zabezpečenie požadovaného publika;

špecifikovanie požadovaného publika;

Účtovanie prechodov medzi budovami;

Spájanie skupín do prúdov pre ľubovoľný súbor disciplín;

Rozdelenie do podskupín;

Po zostavení rozvrhu v prípade potreby vymeňte učiteľov alebo zmeňte čas hodiny.

Okrem toho sú pre každú univerzitu stanovené aj špecifické požiadavky na funkčnosť softvérového produktu.

Možnosti podľa môjho názoru najpopulárnejších softvérových produktov na ruskom trhu sú uvedené v prílohe 1.

Z uvedeného zoznamu azda len program „Metodista“ viac-menej zodpovedá požadovanej funkcionalite softvérového produktu na rozvrhovanie na vysokej škole. Tento stav možno ľahko vysvetliť tým, že školské vzdelávanie je dnes viac „štandardizované“ (v zmysle organizácie vzdelávacieho procesu) ako vysokoškolské. Táto štandardizácia vedie k veľkému potenciálnemu trhu pre predaj softvéru a návratnosť vývoja predajom veľkého počtu kópií produktu za relatívne nízku cenu.

V prípade univerzít je dopyt po rozvrhových systémoch možno ešte väčší ako v prípade škôl, vec však komplikuje veľká špecifickosť organizácie vzdelávacieho procesu na každej jednotlivej univerzite. Nie je možné vytvoriť jednotný softvér a náklady na vytvorenie špecializovaného produktu od vývojárov tretích strán sa ukazujú byť neprimerane vysoké. Okrem toho je predpokladom existencia „vyrovnaného“ rozvrhu, ktorý predpokladá možnosť výmeny učiteľov alebo zmeny času vyučovania. Zatiaľ vám to žiadny softvérový produkt neumožňuje celkom jednoducho (hoci Methodist má určité možnosti).

1.3. Formulácia problému.

Cieľom tejto práce bolo vytvoriť matematický model univerzitného rozvrhu, ktorý by umožňoval efektívne (v danom časovom horizonte as danou mierou optimality) riešiť problém automatického rozvrhovania a mal by flexibilitu (drobné zmeny v v prípade zmien vstupných informácií) prispôsobiť systém v rámci konkrétneho praktického problému. Aby sa úloha trochu zjednodušila, v počiatočnej fáze návrhu sa urobili niektoré predpoklady:

Rozvrh je založený na nie viac ako dvoch pároch za deň (čo je celkom vhodné pre večerné kurzy);

Všetky dvojice sa konajú v jednej budove;

Problém spočíva v lineárnom programovaní;

Nevykonáva sa žiadny ďalší rozklad modelu;

Všetky modelové koeficienty a požadované premenné sú celé čísla;

Vzniknutý problém musí byť vyriešený jednou z univerzálnych (nezávislých od celočíselných hodnôt koeficientov) metód celočíselného lineárneho programovania.

2. Vývoj matematického modelu a praktická implementácia automatického systému plánovania 2.1. Matematický model rozvrhovania vysokých škôl

Zostavme si matematický model univerzitného rozvrhu z hľadiska lineárneho programovania. Zavedme notáciu a definujme premenné a obmedzenia.

2.1.1. Označenia

Univerzita má N študijných skupín, spojených do R prúdov; r – číslo toku, r = 1, ..., R, k r – číslo študijnej skupiny v toku r, k r = 1, ..., G r.

Rozdelenie do skupín do vlákien sa vykonáva na základe princípov:

1. Použitie dvoch skupín toho istého učebného fondu na ich prednášky automaticky znamená ich zaradenie do 1 prúdu (predpokladá sa, že všetky prednášky študijných skupín sa konajú spolu).

2. Skupina (alebo jej časť) ako jednotka vzdelávacieho procesu na vysokej škole môže byť zaradená do rôznych prúdov, ale do každého z nich len raz.

3. Počet vlákien nie je obmedzený.

Vyučovanie prebieha v pracovných dňoch v jeden a pol hodinových intervaloch, ktoré budeme nazývať dvojice.

Označme:

t – číslo pracovného dňa v týždni, t Є T kr, kde

T kr – súbor čísel pracovných dní pre skupinu k r;

j – číslo páru, j = 1 ,…, J;

J – celkový počet párov.

S každou študijnou skupinou k r prúd r počas týždňa sa podľa učebných osnov vedú hodiny W kr, z toho S r prednášky a Q kr praktické. Označme:

s r – číslo disciplíny v zozname vyučovacích hodín pre prúd r, s r = 1 ,…,S r ;

q kr – číslo disciplíny v zozname praktických cvičení pre skupinu k r, q kr = 1,…, Q kr.

Predpokladá sa, že prednášky sa konajú pre všetky skupiny prúdu súčasne a v tej istej učebni. Potom, ak sa v disciplíne počas týždňa vyučuje viac ako jedna vyučovacia hodina, táto disciplína sa uvedie v zozname prednášok alebo praktických hodín toľkokrát, koľkokrát je to stanovené v učebných osnovách pre každý prúd alebo skupinu.

UČITELIA

Nech p je číslo (meno) učiteľa, p = 1 ,…, P. Predstavme si booleovské hodnoty a :

Vyučovacia záťaž učiteľov sa plánuje pred zostavením rozvrhu triedy, v dôsledku čoho možno v tejto fáze považovať hodnoty za dané. Pre každého učiteľa p, p = 1 ,…,P je špecifikované aj jeho zaťaženie triedy - N p hodín týždenne.

KONTROLNÝ FOND

Vyučovanie v každom prúde sa môže konať iba v určitých triedach (napríklad praktické hodiny informatiky sa môžu konať iba v ukážkových triedach). Nechať byť:

(A 1 r ) – súbor publika pre prednášky na streame r;

(A 2 r) – súbor učební praktického vyučovania na toku r;

A 1 r – počet prvkov množiny (A 1 r);

A 2 r – počet prvkov množiny (A 2 r);

A 1 r + A 2 r – počet divákov spojenia množín (A 1 r )∩(A 2 r ).

Divácky fond sa určuje pred začiatkom plánovania, takže súbory možno považovať za dané.

2.1.2. Premenné

Úlohou rozvrhu je určiť pre každú prednášku (na streame) a praktickú hodinu (v skupine) deň v týždni a dvojicu na tento deň, pričom treba brať do úvahy splnenie nižšie konštruovaných obmedzení a minimalizáciu určitú objektívnu funkciu.

Predstavme si nasledujúce povinné booleovské premenné:

=

V prípade plánovania pre skupiny večerných kurzov je J=2. Zovšeobecnenie modelu na všetky formy učenia nájdete na strane 669.

2.1.3. Obmedzenia

Pre každú skupinu k r musia byť počas týždňa dokončené všetky typy triednych prác:

Každá prednáška s r a praktická lekcia q kr pre všetky prúdy r a všetky skupiny k r sa môžu konať najviac raz v ktorýkoľvek deň t:

Ak premenné spájajú všetky typy činností s časom ich realizácie, tak produkty a spojiť čas s menom učiteľa.

V každý deň t a v každej dvojici j môže učiteľ p odučiť najviac jednu vyučovaciu hodinu v jednej disciplíne v jednom prúde alebo v jednej skupine:

Napokon, v každý deň v každej triede by počet prednášok a praktických hodín nemal presiahnuť fond triedy dostupný na univerzite:

Okrem toho musia byť pre všetky množiny pretínajúcich sa množín (A 1 r) a (A 2 r) splnené tieto podmienky:

Prezentované vzťahy vyčerpávajú bezpodmienečné obmedzenia, ktoré sa vždy berú do úvahy pri zostavovaní harmonogramu. Môžu však existovať špecifické podmienky, predovšetkým vykonávanie určitých druhov prác vo „vyššom“ alebo „dolnom“ týždni (t.j. jedna akademická hodina týždenne). Iné špeciálne podmienky nemožno vylúčiť, ale pre zjednodušenie modelu sa s nimi nepočítalo.

2.1.4. Objektívna funkcia

Aby mohol vysokoškolský učiteľ v plnom rozsahu vykonávať vedeckú, pedagogickú a metodickú prácu a pripravovať sa na vyučovanie, musí mať voľný čas. Táto podmienka nie je postačujúca, ale nevyhnutná. Je zrejmé, že by mal mať voľný čas nie v „roztrhanom“ režime, ako sú napríklad „okná“ medzi triedami so študentmi, ale ak je to možné, v úplne voľných pracovných dňoch. To je ekvivalentné maximalizácii pracovného zaťaženia učiteľov v dňoch, keď ho majú (pozri (5)). Zároveň však majú učitelia nerovnaké nároky na voľný čas, keďže majú rozdielny tvorivý potenciál. Preto je potrebné zaviesť váhové koeficienty, ktorými by sa malo zohľadňovať zodpovedajúce postavenie učiteľa – jeho akademické tituly a titul, zastávaná funkcia, vedecká a spoločenská činnosť atď. V niektorých prípadoch je na základe odborných posudkov možné použiť individuálne váhové koeficienty, ktoré zohľadňujú iné faktory.

Zvolíme teda kritérium kvality rozvrhovania vyučovania v podobe maximalizácie váženého počtu dní bez práce v triede pre všetkých učiteľov, čo pri pevne stanovenej dĺžke pracovného týždňa zodpovedá maximálnemu celkovému zhusteniu zaťaženie triedy.

Uvažujme výraz pre hodnotu zaťaženia triedy v deň t učiteľa p:

kde M je ľubovoľné kladné dostatočne veľké číslo; - požadovaná boolovská premenná.

Z (10) vyplýva, že ak , potom = 1 a ak , potom = 0.

Ak vezmeme do úvahy vyššie uvedený vecný význam optimalizačného kritéria v dodatočných obmedzeniach (10), ako aj zavedením váhových koeficientov učiteľského statusu, získame požadované kritérium optimality:

Zavedená účelová funkcia nie je jediná možná. Zavedením ďalších objektívnych funkcií sa nemení obmedzenia matematického modelu a metód riešenia úlohy, ale môže výrazne ovplyvniť výsledky výpočtov.

2.2. METÓDY RIEŠENIA PROBLÉMU

Problém maximalizácie lineárnej cieľovej funkcie uvedený v predchádzajúcom odseku pod daným systémom obmedzení je problém lineárneho celočíselného booleovského programovania, pretože všetky koeficienty obmedzenia sú celočíselné kvôli diskrétnej povahe počiatočných údajov problému; Navyše požadované premenné matematického modelu môžu nadobúdať len dve hodnoty. V súčasnosti existuje niekoľko možných spôsobov riešenia tohto typu problému.

B – metódy usporiadaného indexovania a modifikovaného značenia sú popísané na základe Lagrangeovho rozkladu pôvodného modelu na množstvo jednoriadkových problémov riešených metódami radenia indexovania alebo modifikovaného značenia. Bohužiaľ, počet operácií každej metódy neumožňuje polynomický odhad; Navyše, s rastúcou dimenziou riešeného problému prudko narastá rozmer tabuľky množín (medzihodnoty) metód, čo je v našom prípade neakceptovateľné. Možno zmena algoritmu rozkladu pre konkrétny matematický model zníži veľkosť tabuliek, ale takýto algoritmus zatiaľ neexistuje.

V tejto súvislosti boli zvolené metódy riešenia opísané v modifikácii simplexnej metódy pre prípad celočíselnej úlohy lineárneho programovania. Vo všeobecnom prípade počet operácií simplexovej metódy neumožňuje polynomický odhad (dokonca bola ukázaná trieda problémov, pre ktoré je počet operácií O(e n)), ale pre prípad nášho problému priemerný počet operácií umožňuje polynomický odhad: O(n 3 m 1/( n-1)) (n – počet premenných; m – počet obmedzení).

2.2.1. ALGORITHM FULL INTEGER

Tento algoritmus sa nazýva úplne celočíselný, pretože ak pôvodná tabuľka pozostáva z celočíselných prvkov, potom všetky tabuľky vyplývajúce z algoritmu obsahujú iba celočíselné prvky. Podobne ako pri duálnej simplexovej metóde, algoritmus začína od duálne prípustnej tabuľky. Ak a i 0 (i = 1 ,..., n+m; a i 0 sú koeficienty účelovej funkcie) sú nezáporné celé čísla, potom je problém vyriešený. Ak je pre nejaký reťazec i 0

Nech je daný celočíselný problém lineárneho programovania:

maximalizovať

za podmienok

Podmienky (12) možno zapísať ako

Predpokladajme, že pre t=0 (t.j. pre pôvodnú tabuľku) sú všetky a ij celé čísla a stĺpce (j = 1 ,..., n) sú lexikograficky kladné. Potom všetky stĺpce zostanú lexikograficky pozitívne počas celého výpočtu.

Pred predstavením metódy na získanie dodatočného obmedzenia z generujúceho reťazca zavedieme novú reprezentáciu čísel. Nech [x] označuje najväčšie celé číslo nie väčšie ako x. Pre akékoľvek číslo y (kladné alebo záporné) a kladné môžeme napísať:

kde (r y je nezáporný zvyšok pri delení y číslom ). najmä . Preto ak , potom r = 1. Ak , potom r = 0.

Zavedená dodatočná nerovnosť musí byť splnená pre akékoľvek celočíselné riešenie úlohy (12). Zvážte nejakú rovnicu v t-tabuľke (s vynechaním indexu riadka) s 0

kde x je zodpovedajúca zložka vektora a sú aktuálne nezákladné premenné. X, a 0 a a j môžeme vyjadriť pomocou znázornenia (14) uvedeného vyššie:

Nahradením výrazov (16) a (17) do (15) a preusporiadaním výrazov dostaneme:

Keďže , a premenné x a podliehajú požiadavke nezápornosti, ľavá strana rovnice (18) je vždy nezáporná. Zvážte výraz na pravej strane, uzavretý v zložených zátvorkách. Koeficienty v tomto výraze sú celé čísla a premenné podliehajú požiadavke na celé číslo. Preto musí byť celý výraz v zátvorkách celé číslo. Označme to s, t.j.

.

Celočíselná slabá premenná s je nezáporná. Ak by totiž s bolo záporné, t.j. by nadobudli hodnoty -1, -2, ..., potom vynásobením by bola celá pravá strana rovnice (18) negatívna, zatiaľ čo ľavá strana je nezáporná.

Zoberme si dva prípady a . Pre a . Dosadením výrazu pre x z (15) do rovnice (19) dostaneme:

Rovnica (21) musí byť splnená pre akékoľvek celočíselné riešenie problému (12). Všimnite si, že ak je 0 v rovnici (21). Preto môže byť rovnica (21) použitá ako vodiaca čiara v simplexnej metóde. Predovšetkým môžete vždy zvoliť dostatočne veľkú veľkosť, aby sa vodiaci prvok v riadku (21) rovnal –1, čím sa zachová celé číslo tabuľky. Výber vhodného z nich ovplyvní rýchlosť konvergencie algoritmu. Najprv si popíšme samotný algoritmus. Ako počiatočné je potrebné vziať duálne realizovateľné riešenie, ktoré možno získať pridaním obmedzenia x n + m+1 =M – x 1 - - … - x n 0, kde M je dostatočne veľká konštanta a urobte jednu iteráciu s pridaným riadkom a s lexikograficky minimálnym stĺpcom , braný ako vodiaci znak. Algoritmus pozostáva z nasledujúcich krokov:

Krok 0. Začnite s duálne prípustnou maticou A 0 v rovnici (13), ktorej prvky sú celé čísla (matica A 0 môže obsahovať aj neceločíselné prvky, pozri o tom na strane 306).

Krok 1. Medzi riadkami s a i 0 0 (i=1, ..., n+m) je problém vyriešený.)

Krok 2. Vyberte (pravidlo výberu bude popísané neskôr) a napíšte ďalší riadok v spodnej časti tabuľky

Táto čiara je vybraná ako vodiaca čiara.

Krok 3. Vykonajte krok duálnej simplexnej metódy, prečiarknite ďalší riadok a vráťte sa na krok 1.

Pre dôkaz konečnosti algoritmu pozri str. 303-304.

Pravidlo výberu je formulované nasledovne.

Krok 0. Nechajte generovať riadok s číslom v.

Krok 1. Nech je lexikograficky minimálny stĺpec medzi stĺpcami s vj

Krok 2. Pre každé a vj je najväčšie celé číslo také, že (lexikograficky menej).

Krok 3. Nech , a (generuje riadok v). Potom

.

Krok 4. Dajte za vj

Vyššie popísané pravidlo výberu umožňuje, aby sa vodiaci prvok rovnal -1, pričom sa zachová duálna platnosť tabuľky a zároveň sa nulový stĺpec čo najviac lexikograficky zredukuje.

2.2.2 Algoritmus priameho celočíselného programovania

Pojem „priamy“, keď sa použije na algoritmus celočíselného programovania, sa vzťahuje na metódu, ktorá vedie k optimálnemu riešeniu získaním postupne „zlepšiteľných“ riešení. Každé z týchto riešení je platné v tom zmysle, že spĺňa lineárne obmedzenia aj podmienku celého čísla. Jednou z pravdepodobných výhod algoritmu je možnosť prerušiť výpočty pred dosiahnutím optimálneho riešenia a použiť najlepšie získané riešenie ako približné. Okrem toho môže byť priamy algoritmus použitý v spojení s duálnymi algoritmami na vytvorenie rôznych kompozitných algoritmov, ktoré môžu prejsť z fázy, ktorá vytvára duálne realizovateľné riešenia, do fázy, ktorá produkuje priamo realizovateľné riešenia.

Prirodzeným precedensom pre priamy algoritmus je celočíselný Gomoriho algoritmus, pretože proces tohto algoritmu vytvára postupnosť duálne realizovateľných celočíselných riešení. Treba pripomenúť, že úplne celočíselný Gomoriho algoritmus je modifikáciou duálnej simplexovej metódy. Hlavným rozdielom tohto algoritmu je, že vedúca struna je rez Gomori s vodiacim prvkom -1. Tento rez sa získa z generujúcej struny, ktorá je definovaná ako jedna z možných vedúcich strún v duálnej simplexovej metóde. Použitie takéhoto rezu ako vedúceho riadku zachová dvojitú platnosť a integritu tabuľky po iterácii.

Ukazuje sa, že môžete podobne upraviť simplexnú metódu tak, aby ste získali algoritmus, ktorý zachováva priamu prípustnosť a celistvosť tabuliek. Ak chcete opísať postup výpočtu, zvážte nasledujúci problém celočíselného programovania:

maximalizovať

Predpokladajme, že stĺpec je vybraný ako vedúci a riadok v je vedúci riadok v iterácii simplexnej metódy, t.j. pre všetky riadky I, v ktorých a je >0. Pred vykonaním Gaussovej eliminačnej procedúry v simplexnej metóde pridáme do tabuľky Gomoriho medznú hodnotu získanú z riadku v:

kde J je množina indexov nebázických premenných v (22), s k je nová (základná) slabá premenná a je neurčitá (dočasne) kladná konštanta.

Všimnite si, že ak nastavíme = a vs, cutoff (23) bude mať dve dôležité vlastnosti. po prvé,

To znamená, že priama platnosť tabuľky je zachovaná, ak ako úvodný riadok použijeme cutoff (23). Po druhé, t.j. vodiaci prvok je 1 (ak sa ako vodiaci reťazec používa klip). Dá sa ľahko overiť (skúmaním vzorcov na zmenu základných premenných), že transformácia simplexnej tabuľky s jediným vodiacim prvkom zachováva celočíselný počet prvkov simplexnej tabuľky.

Tieto myšlienky slúžili ako základ pre priamy algoritmus v celočíselnom programovaní:

Krok 0. Začnite so stĺpcovou tabuľkou, v ktorej a i 0 0 (i 1) a všetky prvky a 0 j, a ij a a i 0 sú celé čísla.

Krok 1. Skontrolujte, či sú podmienky a 0 j 0 (j 1); ak sú spokojní, tak koniec, súčasné základné riešenie je optimálne; ak nie, prejdite na krok 2.

Krok 2. Vyberte vedúci stĺpec s s 0 s 0. Tento riadok slúži ako generátor pre rez Gomori.

Krok 3. Získajte odrezok Gomori z tvoriacej linky a pridajte ho na spodok tabuľky, t.j. pridajte rovnicu (23) k obmedzeniam problému, kde .

Krok 4. Preveďte tabuľku pomocou rezu (23) ako vedúceho radu. Slabá premenná s k in (23) sa stane nebázickou. Vráťte sa na krok 1.

Pre dôkaz konečnosti algoritmu pozri str. 346-353.

Keďže výber generujúceho reťazca nie je triviálna úloha, zdá sa, že musí existovať niekoľko reťazcov, ktoré môžu slúžiť ako generujúce reťazce. V úvodných argumentoch bola ako generujúca čiara použitá vodiaca čiara simplexovej metódy. Táto čiara vždy vytvára hranicu, ktorá je vedúcou čiarou s vedúcim prvkom rovným jednej. V tabuľke sú zrejme ďalšie riadky, z ktorých možno získať rezy s rovnakými vlastnosťami. Predpokladajme, že hranica sa získa podľa vzorca:

kde sa určuje z podmienky

Definujme množinu V(s) ako súbor riadkov spĺňajúcich podmienku (25).

Nasledujúce dve pravidlá sú príkladmi platných pravidiel výberu reťazca generovania:

Pravidlo 1.

1. Zostavte sekvenčný konečný zoznam indexov riadkov tak, aby sa index každého riadka v ňom objavil aspoň raz. Prejdite na 2.

2. Ak je zoznam prázdny alebo neobsahuje žiadny index z V(s), vráťte sa na 1.; v opačnom prípade nájdite prvý index v V(s) v zozname. Vyberte riadok v ako produkciu. Výstup indexu v a všetkých predchádzajúcich indexov zo zoznamu. Prejdite na 3.

3. Dôsledne vyberte reťazec v prevzatý v 2. ako generujúci až do v V(s). Raz v V(s), vráťte sa na 2.

Pravidlo 2.

1. Nech V t (s) je množina V(s) zodpovedajúca t-tej tabuľke. Ak V t (s) obsahuje viac ako jeden prvok: V t (s) = (v 1, v 2, ..., v k +2), potom ako generátor vyberte riadok tak, aby v postupnosti množín V 1 (s 1), V 2 (s 2), ..., V t (s) čiara sa objavila skôr (nie neskôr) ako ostatné a potom zostala až do V t (s); prejsť na 2.

2. Dôsledne vyberte reťazec v prevzatý v 1. až . Raz sa vráťte na 1.

2.2.3. TECHNIKA NA ZÍSKANIE PÔVODNÉHO POVOLENÉHO ZÁKLADU

Každá z vyššie uvedených metód môže byť vyriešená iba vtedy, ak je problém lineárneho programovania buď priamo alebo duálne realizovateľný. Takáto prípustnosť znamená prítomnosť počiatočného prípustného základu v pôvodnom probléme. Ak je problém realizovateľný priamo aj duálne, potom je výsledné riešenie optimálne. Vo väčšine prípadov sa po nastolení problému ukáže, že nie je prípustný ani priamo, ani duálne. Preto uvádzame algoritmus na získanie počiatočného prípustného základu.

Nechajte problém lineárneho programovania napísať v kanonickej forme:

minimalizovať

za podmienok

Všetky b i môžu byť nezáporné vynásobením, ak je to potrebné, zodpovedajúcej rovnice –1. Potom môžete do každej rovnice pridať umelú premennú (umelé premenné musia byť nezáporné) takým spôsobom, aby sa z umelých premenných vytvoril počiatočný základ:

Umelé premenné možno odvodiť zo slabých premenných používaných na premenu nerovností na rovnice. V skutočnosti, ak sú počiatočné obmedzenia problému lineárneho programovania dané vo forme nerovností:

potom pridaním slabej premennej ku každej nerovnosti dostaneme:

Ak b i 0, potom s i možno použiť ako počiatočné základné premenné.

Rozdiel medzi umelými premennými a slabými premennými s i je nasledovný. Pri optimálnom riešení úlohy musia byť všetky umelé premenné rovné nule, keďže v pôvodnom probléme takéto premenné nie sú. Na druhej strane je dosť možné, že v optimálnom riešení budú mať slabé premenné kladné hodnoty. Aby sa umelé premenné stali nulovými, účelová funkcia môže byť reprezentovaná takto:

kde M i sú dostatočne veľké kladné čísla. Myšlienka metódy zodpovedá skutočnosti, že umelé premenné majú zjavne vysoké ceny. Táto metóda vedie k nulovým hodnotám umelých premenných v optimálnom riešení.

Existuje ďalší spôsob, ako získať počiatočný prípustný základ. V tejto metóde, rovnako ako v prvej, sa ako počiatočné základné premenné používajú umelé premenné. Uvažuje sa o novej účelovej funkcii, ktorá je súčtom umelých premenných. Je potrebné minimalizovať používanie z-rovnice ako jedného z obmedzení. Ak má pôvodný systém rovníc realizovateľné riešenie, potom sa všetky umelé premenné musia rovnať nule. Preto musí byť minimálna hodnota nula. Ak , potom pôvodný systém rovníc nemá žiadne prípustné riešenia. Ak , potom môžeme vynechať účelovú funkciu a použiť optimálny základný tvar ako počiatočný realizovateľný základ pre minimalizáciu z. V literatúre sa táto metóda nazýva dvojfázová simplexová metóda. V prvej fáze metódy sa nájde prípustný základ minimalizáciou, v druhej sa z minimalizuje a získa sa optimálny základ.

Zvážte nasledujúci problém lineárneho programovania ako príklad:

minimalizovať

za podmienok

kde všetky b i sú nezáporné.

Ak zavedieme umelé premenné a novú účelovú funkciu, dostaneme nasledujúci problém:

minimalizovať

,

za podmienok

Ak odčítame všetky rovnice obsahujúce b i od -tvaru, dostaneme:

-z

kde Systém (26) je diagonálny vzhľadom na Prvá fáza simplexovej metódy pozostáva z minimalizácie za podmienok (26). Na znamenie z neexistujú žiadne obmedzenia. V procese výpočtov, akonáhle sa umelá premenná stane nebázickou a jej koeficient v -forme je kladný, samotná premenná a zodpovedajúci stĺpcový vektor sú vylúčené z ďalších výpočtov.

2.3. VLASTNOSTI PRAKTICKEJ IMPLEMENTÁCIE SYSTÉMU

V praxi nie je veľmi vhodné pracovať s informáciami vo forme, v akej sú definované v matematickom modeli. Preto sa najprv rozhodnime pre spôsob usporiadania údajov alebo dátového modelu.

2.3.1. VÝBER MODELU

Dátový model je súbor dohôd o metódach a prostriedkoch formalizácie popisu objektov a ich vzťahov súvisiacich s automatizáciou systémových procesov. Typ modelu a typy dátových štruktúr v ňom použitých odrážajú koncepciu organizácie a spracovania dát používanú v DBMS, ktorá model podporuje, alebo v jazyku programovacieho systému, v ktorom je vytvorený aplikačný program na spracovanie dát.

Na vyriešenie tohto problému je potrebné vytvoriť dátový model, v ktorom by bolo množstvo pomocných informácií minimálne, bola by zásadná možnosť viacužívateľského prístupu k dátam a bola by zabezpečená vysoká úroveň ochrany dát.

V súčasnosti existujú tri hlavné prístupy k formovaniu dátového modelu: hierarchický, sieťový a relačný.

HIERARCHICKÝ SPÔSOB ORGANIZÁCIE

Hierarchická databáza pozostáva z usporiadanej množiny stromov; presnejšie z usporiadanej množiny viacerých inštancií rovnakého typu stromu. Typ stromu pozostáva z jedného typu „koreňového“ záznamu a usporiadanej množiny nula alebo viacerých typov podstromu (každý z nich je typ stromu). Stromový typ je vo všeobecnosti hierarchicky usporiadaná kolekcia typov záznamov.

Integrita väzieb medzi predkami a potomkami je automaticky zachovaná. Základné pravidlo: žiadne dieťa nemôže existovať bez svojho rodiča. Všimnite si, že podobné udržiavanie referenčnej integrity medzi záznamami, ktoré nie sú súčasťou rovnakej hierarchie, nie je podporované.

SIEŤOVÝ SPÔSOB ORGANIZÁCIE

Sieťový prístup k organizácii údajov je rozšírením hierarchického prístupu. V hierarchických štruktúrach musí mať podriadený záznam práve jedného predka; v sieťovej dátovej štruktúre môže mať dieťa ľubovoľný počet predkov.

Sieťová databáza pozostáva zo sady záznamov a sady spojení medzi týmito záznamami, presnejšie zo sady inštancií každého typu zo sady typov záznamov špecifikovaných v schéme databázy a sady inštancií každého typu z daný súbor typov pripojenia.

Typ vzťahu je definovaný pre dva typy záznamov: predok a potomok. Inštancia typu vzťahu pozostáva z jednej inštancie typu záznamu predchodcu a usporiadanej množiny inštancií podriadeného typu záznamu. Pre daný typ prepojenia L so záznamom predka typu P a podriadeným záznamom typu C musia byť splnené tieto dve podmienky:

1. Každá inštancia typu P je predkom iba jednej inštancie L;

2. Každá inštancia C je potomkom najviac jednej inštancie L.

VZŤAHOVÝ SPÔSOB ORGANIZÁCIE

Hlavné nevýhody hierarchických a sieťových typov dátových modelov sú:

1. Príliš ťažké použitie;

2. V skutočnosti sa vyžaduje znalosť fyzickej organizácie;

3. Aplikačné systémy závisia od tejto organizácie;

4. Ich logika je preťažená detailmi organizácie prístupu k databáze.

Zdá sa, že najbežnejšou interpretáciou relačného dátového modelu je Dat, ktorý ho reprodukuje (s rôznymi vylepšeniami) takmer vo všetkých svojich knihách. Podľa Date sa relačný model skladá z troch častí, ktoré opisujú rôzne aspekty relačného prístupu: štrukturálna časť, manipulačná časť a holistická časť.

Štrukturálna časť modelu uvádza, že jediná dátová štruktúra používaná v relačných databázach je normalizovaná n-árna relácia.

Manipulačná časť modelu potvrdzuje dva základné mechanizmy manipulácie s relačnými databázami – relačná algebra a relačný kalkul. Prvý mechanizmus je založený hlavne na klasickej teórii množín (s určitými vylepšeniami) a druhý je založený na klasickom logickom aparáte predikátového počtu prvého rádu. Hlavnou funkciou manipulačnej časti relačného modelu je poskytnúť mieru relatívnosti akéhokoľvek špecifického relačného databázového jazyka: jazyk sa nazýva relačný, ak nie je menej expresívny a výkonný ako relačná algebra alebo relačný kalkul.

A nakoniec, integrálna časť relačného dátového modelu stanovuje dve základné požiadavky na integritu, ktoré musia byť podporované v akomkoľvek relačnej DBMS. Prvá požiadavka sa nazýva požiadavka integrity entity. Druhá požiadavka sa nazýva požiadavka referenčnej integrity.

Po predbežnej analýze matematického modelu systému a metód organizácie údajov, ako aj softvéru dostupného na trhu (hierarchické a sieťové metódy organizácie naznačujú objektovo orientovaný prístup k organizovaniu údajov a dnes existujú takéto DBMS (napr. napríklad Jasmin alebo Informix Dynamic Server), ale na V čase vývoja neexistovala možnosť ich použitia, zároveň však existujú veľmi „výkonné“ relačné DBMS (napríklad Oracle 8i)) výber bol urobený v prospech relačného spôsobu organizácie ukladania údajov.

2.3.2. POPIS VSTUPNÝCH INFORMÁCIÍ

Všetky informácie potrebné na vyriešenie problému sú špecifikované pred začiatkom iterácií metód na riešenie problému plánovania. Pre zjednodušenie sa predpokladá, že uvedené informácie sú konštantné počas celého obdobia, na ktoré sa harmonogram pripravuje.

Bez straty určitej miery všeobecnosti úlohy je možné určiť určitý súbor vstupných údajov potrebných na vytvorenie obmedzení a riešenie problému a súčasne spoločných pre všetky druhy praktických implementácií systému. Vzhľadom na špecifiká úlohy (možnosť relatívne ľahkého prispôsobenia matematického modelu pre prípad praktickej implementácie v rámci konkrétnej univerzity) neboli vypracované formy vstupných informačných dokumentov. Podrobnosti o vstupných informáciách sú popísané v tabuľke 2.

Tabuľka 2. Popis podrobností o vstupných informáciách

Názov podrobností	Charakteristika detailov
vstupné dokumenty	Typ	Max. dĺžka	Presnosť
Priezvisko, meno, priezvisko učiteľa; Kontaktné telefónne číslo učiteľa; Akademický titul; Akademický titul; Názov skupiny; Počet členov skupiny; názov vyučovaného kurzu; Počet hodín v triede; čísla divákov; informácie o publiku; Názov predmetu vyučovaného učiteľom; Číslo skupiny, kde sa predmet číta; Informácie o publiku, kde sa predmet číta.

Okrem týchto údajov si matematický model vyžaduje prítomnosť niektorých dodatočných údajov, ktoré je možné získať po analýze vstupných informácií programovo.

2.3.3. ROZVOJ INFORMAČNEJ PODPORY PRE ÚLOHU

Budeme analyzovať zdrojové informácie s cieľom určiť zloženie a štruktúru informácií pre následnú formalizáciu a konštrukciu informačného a logického dátového modelu (ILM). Vyššie uvedený matematický model, ako aj ďalšie informácie z popisu predmetnej oblasti nám umožňujú určiť úlohu detailov vo vzájomne súvisiacich informáciách obsiahnutých v dokumente. Na základe tejto analýzy stanovíme funkčné závislosti detailov v súlade s odporúčaniami a požiadavkami na normalizáciu dát, následne vykonáme samotnú normalizáciu. Účelom normalizácie je znížiť (ale nie nevyhnutne odstrániť) redundanciu údajov. Niekedy sa však zámerne vytvorí určitá redundancia údajov, aby sa zlepšila efektivita programu. Definujme tri formy normalizácie databázy.

Tabuľka je v prvej normálnej forme (1NF), ak má primárny kľúč, všetky atribúty sú jednoduché dátové typy a neexistujú žiadne duplicitné atribúty. Aby boli v súlade s 1NF, domény atribútov musia byť atómové hodnoty a nesmú existovať žiadne duplicitné skupiny atribútov. Všetky duplicitné skupiny atribútov musia byť presunuté do novej tabuľky.

Tabuľka je v druhej normálnej forme (2NF), keď je v prvej normálnej forme a každý nekľúčový atribút je plne funkčne závislý od primárneho kľúča (t. j. v 2NF musí byť každý nekľúčový atribút úplne závislý od polí primárny kľúč).

Tabuľka je v tretej normálnej forme (3NF), ak je v 2NF a nemá žiadne tranzitívne závislosti. Tranzitívne závislosti sú funkčné závislosti medzi nekľúčovými atribútmi. Akýkoľvek nekľúčový atribút, ktorý je funkčne závislý od iného nekľúčového atribútu tej istej tabuľky, vytvára prechodnú závislosť a musí byť presunutý do inej tabuľky.

Výsledné funkčné závislosti sú celkom triviálne a zjavne vyplývajú z matematického modelu, preto ich v ďalšom popise neuvádzame. V nasledujúcej prezentácii sú tiež vynechané stredné stupne normalizácie. Preto uvádzame len finálny infoologický model databázy (pozri obr. 1.).

Obr.1. Infologický model databázy pre úlohu plánovania tried

2.3.4. ZNAKY OBMEDZENÍ VYTVORENIA MATEMATICKÉHO MODELU PROBLÉMU ROZVRHU

Zostavenie obmedzení (1) – (7) matematického modelu problému plánovania je pomerne triviálna úloha, ktorú je možné vyriešiť pomocou jednoduchých SQL dotazov a nevyžaduje predbežnú analýzu vstupných informácií. Preto sa podrobnejšie zastavíme len pri obmedzeniach formulára (8).

Všimnite si, že v matematickom modeli systému nie je čítaný predmet „viazaný“ na konkrétne publikum, ale na určitý súbor cieľových skupín. Umiestnenie konkrétnych čísel publika sa uskutoční po vyriešení úlohy. Obmedzenia formy (8) majú zmysel len vtedy, keď sa množiny publika pretínajú. V matematickom modeli systému sa navrhuje brať do úvahy všetky jedinečné pretínajúce sa dvojice vo forme obmedzení. Počet týchto križovatiek môže byť veľký, čo môže viesť k veľkému počtu dodatočných obmedzení, ktoré negatívne ovplyvňujú rýchlosť optimalizačných algoritmov. Počet dodatočných obmedzení sa však dá výrazne znížiť.

Uvažujme prípad lineárneho usporiadania pretínajúcich sa množín (pozri obr. 2).

Obr.2. Lineárne sa pretínajúce množiny

V prípade takéhoto usporiadania súborov učební na vedenie vyučovania bude celkový počet obmedzení formulára (8) n-1, kde n je počet súborov. Vyššie opísané usporiadanie pretínajúcich sa množín možno nazvať lineárne, pretože v tomto prípade je n pretínajúcich sa množín usporiadaných akoby v rade. Môžeme uvažovať o prípade, keď sa množiny vzájomne pretínajú ľubovoľným spôsobom (pozri obr. 3.).

Obr.3. Ľubovoľne sa križujúce množiny

Počet obmedzení tvaru (8) v tomto prípade možno znížiť vytvorením týchto obmedzení analogicky ako v prípade lineárneho usporiadania množín. Na tento účel je potrebné predpokladať, že napríklad množiny B a D pretínajúce sa s A sú jednou množinou, určiť oblasť priesečníka takejto množiny s množinou A a potom vykonať rovnaké akcie s výsledným oblasť križovatky.

Viac informácií nájdete na strane 210.

2.4. Výsledky programu

Pri praktickej implementácii systému bola osobitná pozornosť venovaná úlohe napísať „jadro“ systému – metódy riešenia problému a postupy pri vytváraní obmedzení. Keďže cieľom nebolo napísať plne funkčný komerčný produkt, časť rozhrania bola napísaná za účelom testovania jadra a určenia hraníc použiteľnosti algoritmov, preto obsahuje minimum funkcionality a neobsahuje moduly na predspracovanie vstupných dát.

Jadro systému a rozhranie boli napísané v Delphi 6.0. Metódy riešenia a algoritmy na vytváranie obmedzení sú napísané pomocou objektovo orientovaných technológií, čo v budúcnosti umožní ich jednoduché zapuzdrenie do ďalších úprav systému bez narušenia integrity interakcie rôznych algoritmov. Text objektových metód riešenia problému je uvedený v prílohe 2. Databáza bola implementovaná na Oracle 8i DBMS, dotazy do nej sú realizované v jazyku PL/SQL.

Údaje počiatočnej úlohy sa vkladajú do databázových tabuliek pomocou formulárov žiadostí. Jedna z týchto foriem je znázornená na obr. 3.

Obr.3. Formulár na zadanie počiatočných údajov

Údaje získané v dôsledku riešenia úlohy nestačia na zobrazenie rozvrhu hodín ihneď po vyriešení úlohy, preto bol napísaný modul na následné spracovanie údajov. Konečný rozvrh hodín je zobrazený vo forme tabuľky, ktorej príklad je na obr. 4.

Ryža. 4. Príklad rozvrhu triedy

Algoritmy na riešenie problému boli testované na rôznych vzorkách zdrojových údajov. Testovanie prebiehalo na počítači s procesorom Intel Pentium 350 MHz, Oracle 8i DBMS bol nainštalovaný na dvojprocesorovom serveri: 2 CPU Intel Pentium II 350 MHz, RAM 384 MB; Ako komunikačný kanál bola použitá LAN so šírkou pásma až 100 Mbit/s. Ako testovacie zdrojové dáta sme použili tak reálne dáta o skupinách, učiteľoch a čitateľských predmetoch večernej formy vzdelávania na ChSU za akademický rok 1999/2000, ako aj náhodne generované zdrojové dáta (čitateľným predmetom boli náhodne pridelené publikum tried). V priemere bolo vykonaných 5 až 10 testov pre každý testovaný rozmer zdrojových údajov. V dôsledku toho sme získali údaje uvedené v tabuľke 2. Na obrázku 5 je znázornený graf závislosti priemerného času na vyriešenie úlohy od počtu prečítaných predmetov a počtu skupín.

2.5. Analýza získaných výsledkov

Analýzou získaných údajov môžeme vyvodiť určité závery o funkčnosti algoritmov riešenia a matematického modelu, ich nedostatkoch a oblastiach použitia.

Po prvé, použitý matematický model obsahuje „extra“ obmedzenia, ktorých existencia je spôsobená lineárnym celočíselným modelom; navyše každému predmetu čítanému v streame (stream môže pozostávať z jednej skupiny) je pridelených 12 (pre večerných študentov) premenné, z ktorých každá je booleovská premenná. Po druhé, čas potrebný na vyriešenie problému sa prudko zvyšuje s pribúdajúcimi vstupnými údajmi. K tomu dochádza v dôsledku prudkého nárastu počtu premenných a obmedzení v modeli, v dôsledku čoho sa zväčšuje rozmer polí a tým aj čas potrebný na vyriešenie problému. Po tretie, matematicky formalizovaný problém pokrýva len úlohu vytvorenia rozvrhu pre večerných študentov bez zohľadnenia prechodov medzi budovami. Zohľadnenie dodatočných požiadaviek zvýši počet obmedzení problému, čo negatívne ovplyvní rýchlosť algoritmov riešenia.

Venujme pozornosť zväčšujúcemu sa rozdielu medzi minimálnou a priemernou hodnotou času na vyriešenie úlohy so zväčšujúcim sa rozmerom úlohy. Tento rozdiel korešponduje s tým, ako „úspešne“ (čo najbližšie k optimálnemu) bolo nájdené počiatočné možné základné riešenie problému. Preto sa čas potrebný na vyriešenie problému môže výrazne skrátiť „úspešným“ nájdením počiatočného základného realizovateľného riešenia. Na nájdenie takéhoto riešenia je najlepšie použiť heuristické a dekompozičné algoritmy.

Závery V priebehu práce bol zostavený matematický model rozvrhu VŠ pre prípad večerného vyučovania bez prechodov medzi budovami, boli zvolené metódy riešenia úlohy a vypracovaný model ukladania počiatočných údajov úlohy. Model ukladania zdrojových dát, algoritmus pre matematickú formalizáciu modelu a metódy riešenia boli implementované vo forme softvérových modulov. Rýchlosť algoritmov bola testovaná na heterogénnych súboroch počiatočných dát, na základe čoho boli určené možnosti a oblasti použitia algoritmov.

Na základe výsledkov testovania sa zistilo, že rýchlosť činnosti algoritmov riešenia problémov silne závisí od množstva vstupných informácií a počiatočného prípustného základného riešenia, a preto je výrazne nižšia ako heuristické a dekompozičné algoritmy. Ale v prípade heuristického riešenia sa jeho optimálnosť (riešenia) (resp. dosiahnutie globálneho maxima) dá dokázať iba úplným hľadaním všetkých možných možností (je jasné, že v tomto prípade bude doba chodu algoritmu veľmi dlhé), preto sa iterácie heuristických algoritmov zastavia pri dosiahnutí určitého maxima (nedá sa povedať, či lokálneho alebo globálneho) významu. Riešenie takéhoto algoritmu môže byť blízko k optimálnemu, ale nie optimálnemu. V tomto prípade na dosiahnutie globálneho maxima môžete použiť metódu riešenia uvažovanú v práci, pretože optimum možno dosiahnuť v niekoľkých iteráciách opísaných metód riešenia.

LITERATÚRA

1. Lagosha B.A., Petropavlovskaya A.V. Súbor modelov a metód na optimalizáciu rozvrhu hodín na univerzite // Ekonómia a matematika. metódy. 1993. T. 29. Vydanie. 4.

2. Hu T. Celočíselné programovanie a toky v sieťach. M.: Mir, 1979.

3. Lebedev S.S. Modifikácia Benderovej metódy čiastočného celočíselného lineárneho programovania // Ekonomika a matematika. metódy. 1994. T. 30. Vydanie. 2.

4. Lebedev S.S., Zaslavsky A.A. Použitie špeciálnej metódy vetvenia a väzby na vyriešenie celočíselného zovšeobecneného transportného problému // Ekonomika a matematika. metódy. 1995. T. 31. Vydanie. 2.

5. Záslavský A.A. Použitie stratégie premennej stratifikácie vo všeobecných problémoch celočíselného lineárneho programovania // Ekonomika a matematika. metódy. 1997. T. 33. Vydanie. 2.

6. Lebedev S.S. O metóde radenia indexovania celočíselného lineárneho programovania // Ekonomika a matematika. metódy. 1997. T. 33. Vydanie. 2.

7. Lebedev S.S., Zaslavsky A.A. Upravená metóda označovania pre booleovské programovacie problémy // Ekonomika a matematika. metódy. 1998. T. 34. Vydanie. 4.

8. Záslavský A.A. Kombinovaná metóda na riešenie problémov s batohom // Ekonomika a matematika. metódy. 1999. T. 35. Vydanie. 1.

Dodatok 1. Možnosti softvérových produktov pre plánovacie systémy.

S Systém AUTOR-2+ je určený na rýchle a pohodlné vytváranie rozvrhov hodín a ich udržiavanie počas celého akademického roka.
A VTOR-2+ je univerzálny systém. Existuje niekoľko verzií programu určených pre akúkoľvek vzdelávaciu inštitúciu:

Stredné a odborné (matematické, jazykové a pod.) školy, lýceá, gymnáziá;

Technické školy, školy a vysoké školy;

univerzity s jednou akademickou budovou;

Univerzity s viacerými akademickými budovami (vrátane prestupov medzi budovami).

A VTOR-2+ umožňuje maximálne zjednodušiť a zautomatizovať komplexnú prácu plánovačov. Systém vám pomáha jednoducho vytvárať, upravovať a tlačiť vo forme pohodlných a vizuálnych dokumentov:

Rozvrhy tried (študijné skupiny);

Rozvrhy učiteľov;

Harmonogram učební (kancelárií);

Vzdelávacie plány;

Tarifikácia.

A VTOR-2+ má pekný dizajn a priateľské služby. Program sa dá celkom ľahko naučiť. Existuje podrobný manuál, ktorý popisuje všetky funkcie a spôsoby práce s programom.
P Program beží na akomkoľvek počítači kompatibilnom s IBM, počnúc 486DX so 4 Mb RAM (a vyššou), zaberá približne 1 Mb na pevnom disku. Operačný systém: MS DOS alebo WINDOWS 95/98.
IN Prevádzková doba závisí od veľkosti vzdelávacej inštitúcie a výkonu počítača. Kompletný výpočet a optimalizácia rozvrhu pre stredne veľkú školu (30 tried, 60 učiteľov, dve zmeny) trvá na počítači Celeron-400 cca 15 minút.

P Program sa vyznačuje jedinečným a veľmi výkonným algoritmom na zostavovanie a optimalizáciu rozvrhu. Výsledný automatický rozvrh nevyžaduje prakticky žiadnu manuálnu úpravu, to znamená, že aj pri veľmi zložitých a prísnych obmedzeniach sú všetky možné triedy umiestnené automaticky. Ak sú v zdrojových údajoch nevyriešiteľné rozpory, možno ich zistiť a odstrániť pomocou špeciálnej analytickej jednotky.

A VTOR-2+ vám umožňuje:

Optimalizujte „okná“ v pláne;

Zvážte požadovaný rozsah dní/hodín pre triedy aj učiteľov;

Optimálne je umiestňovať triedy do učební (posluchární) s prihliadnutím na charakteristiky tried, predmetov, učiteľov a kapacity učební;

Berte do úvahy povahu práce a želania zamestnancov na plný úväzok a hodinových pracovníkov na čiastočný úväzok;

Je ľahké spojiť („spárovať“) niekoľko tried (študijných skupín) do prúdov pri vedení akýchkoľvek tried;

Rozdeľte triedy pri vyučovaní cudzieho jazyka, telesnej výchovy, práce, informatiky (a akýchkoľvek iných predmetov) do ľubovoľného počtu podskupín (až desať!);

Zaviesť (okrem hlavných predmetov) špeciálne kurzy a voliteľné predmety;

Optimalizujte jednotnosť a pracovnú náročnosť rozvrhu.

2. Systém „Schedule“ ver 4.0 Moskva – LinTech

Hneď je potrebné poznamenať, že program „Rozvrh“ je zameraný na zostavenie školského rozvrhu, použitie na univerzitách a vysokých školách je možné len s určitými výhradami. Plánovanie sa robí v rámci súboru podmienok, ktoré sú určené v krokoch zadávania počiatočných údajov. Úplný zoznam možných podmienok je uvedený nižšie:

- O maximálny počet lekcií je obmedzený – t.j. maximálny povolený počet hodín za deň;

- R rovnomerné rozdelenie úväzku učiteľov medzi dni rozvrhu;

- R rovnomerné rozloženie triedneho zaťaženia medzi dňami rozvrhu;

- TO monitorovacie okná v rozvrhoch učiteľov;

- P Program berie do úvahy skutočnosť, že triedy sa môžu ľubovoľne spájať a deliť (triedy možno spájať do prúdov alebo deliť na menšie podskupiny a tieto podskupiny zase môžu slúžiť ako základ pre spájanie do väčších skupín. Príklad: v škole č. 1859 Existujú 2 seniorské triedy, ale v každej z týchto tried sú dve podskupiny pre špecializáciu, hodiny všeobecných predmetov sa konajú pre celú triedu naraz a predmety špecializácie oddelene. Ale keďže podskupiny pre špecializáciu sú príliš malé a je málo učiteľov, v niektorých predmetoch sa dajú spájať aj podskupiny 11a a 11b (napr. v cudzom jazyku) - to sťažuje zabezpečenie nadväznosti rozvrhu hodín (treba zabezpečiť nadväznosť rozvrhu pre každú z podskupín);

- N prítomnosť viacerých zmien - v tomto prípade musia jednotlivé triedy prísť neskôr ako skupiny prvej zmeny, navyše sa sťažuje ovládanie okienok v rozvrhu učiteľov, ak sú učitelia pracujúci na obe zmeny - v tomto v prípade, že v rozvrhu týchto učiteľov musia byť ich triedy „zazmluvnené“ okolo priesečníka zmien;

- U podmienka prepojenia učiteľov s publikom – jednotliví učitelia majú „svoje“ publikum, v ktorom vedú všetky svoje hodiny;

- N prítomnosť „plávajúceho“ posunu - keď nie je presne určený čas začiatku prvej hodiny, pretože vytvára sa dynamicky v závislosti od uvoľnenia súvisiacich tried, učiteľov a publika;

- TO sledovanie, či rozvrh objektu (triedy, učiteľa, obecenstva) spadá do prípustného pracovného rozsahu (v mape časových obmedzení). Napríklad pre učiteľa mapa časových obmedzení zvyčajne označuje metodické dni, niekedy jednotlivé čísla hodín - jedným slovom sú uvedené pozície, pre ktoré nie je možné nastaviť triedy s účasťou daného objektu;

- N prítomnosť kombinovaných predmetov – ako napríklad „cudzie jazyky/informatika“, „informatika/práca“ atď. - keď je trieda rozdelená na podskupiny;

- U podmienka prepojenia predmetov na učebne - vedenie vyučovania v jednotlivých predmetoch je možné len v presne vymedzenej učebni alebo zozname učební (telesná výchova, robotníctvo a pod.);

- S opustenie rozvrhu s prihliadnutím na skutočnosť, že v niektorých predmetoch nepríde na vyučovanie celá trieda, ale jej podskupina. Aby sa v tomto čase po škole nepotulovala ďalšia podskupina, takéto triedy môžu byť striktne len prvé alebo posledné triedy v rozvrhu hodín;

- “IN zachovať paralely“ - pre niektorých učiteľov je potrebné vziať do úvahy skutočnosť, že vedenie hodín si vyžaduje dlhodobú prípravu (napríklad hodiny chémie), v tomto prípade sa hodiny v dennom rozvrhu učiteľa snažia usporiadať do blokov. paralely, napr. prvý 5. ročník, potom 7. -y atď., alebo pri rozdeľovaní medzi dňami rozdeľovať triedy v rôznych paralelách na rôzne dni;

- A Niekedy je pri zostavovaní rozvrhu potrebné vziať do úvahy nuansu, že pre niektoré predmety je rozvrh známy vopred - v tomto prípade sú takéto triedy zavedené ako nehybné (pevné);

- TO kontrola zakázaných kombinácií predmetov pripadajúcich na ten istý deň rozvrhu hodín - napríklad je nežiaduce, aby sa „telesná výchova“ a „práca“ vykonávali v ten istý deň;

- IN splnenie podmienky požadovaných sledov predmetov - kedy je potrebné zabezpečiť inštaláciu skupín tried, v ktorých vyučovanie musí prebiehať v určitej postupnosti, napr. fyzika-astronómia a pod.;

- N prítomnosť tried viazaných na učebne - väčšina tried pre takéto triedy sa koná v tejto triede, s výnimkou tých tried, ktoré vyžadujú špecializovanú učebňu;

- N potreba usporiadať hodiny v jednotlivých predmetoch do dvoch tried za sebou („v pároch“, „iskry“), pričom táto podmienka môže byť prísna (v žiadnom prípade nerozbíjať „iskry“ tried), alebo môže byť výhodnejšia (ak nie je možné presunúť dve triedy, „iskra“ sa môže prelomiť);

Zohľadňuje sa skutočnosť, že v niektorých predmetoch je zaradenie povolené len do jednotlivých tried.

3. „Metodistický“ systém

Dostupné v dvoch verziách.

Virtuálna verzia.

Dostupné bez modulu automatického plánovania. Vlastnosti virtuálnej verzie:

Rýchle vyhľadávanie v zoznamoch učiteľov, tried, tried (skupín), odborov, budov;

Získanie referenčných informácií pre každý nájdený prvok zoznamu (kapacita publika, všetky budovy auly X, adresa a telefón učiteľa, zoznam katedry, počet hodín v disciplíne, vyučovacia náplň učiteľa a pod.);

Ovládanie a schopnosť prerozdeľovať hodiny medzi týždňami v akejkoľvek akademickej disciplíne. skupiny;

Automatická kontrola možných chýb pri zadávaní údajov (korešpondencia celkového počtu hodín a typov tried, nezaradenie učiteľov do podskupín, časový rozpočet študijnej skupiny a učiteľa, nesúlad medzi hodinami v prúdových skupinách a pod.);

Schopnosť systematicky ukladať (a rýchlo vyhľadávať) ďalšie (nepotrebné na plánovanie) informácie: fotografie učiteľov, kurátorov študijných skupín (triednych učiteľov), informácie o zástupcoch rodičovských výborov, pozíciách, akademických tituloch a tituloch zodpovedných za publikum, ...

Rýchlo získajte kompletné informácie o kombinácii faktorov (všetky skupiny prúdu, všetky disciplíny učiteľa X, s uvedením pracovnej záťaže podľa týždňa a typu hodín, ktoré disciplíny sa môžu v počítačovej triede vyučovať, osobné želania pre vedenie triedy akéhokoľvek učiteľa, zoznam prázdnin v sýrskej skupine a mnoho ďalšieho atď.);

Možnosť prezerať, tlačiť a upravovať hotový rozvrh s kontrolou správnosti zmien (obsadenosť tried, učiteľov, skupín/podskupín, ...);

Kedykoľvek si môžete objednať modul generovania harmonogramu pre pripravené dáta;

Plán sa generuje na vašom počítači s možnosťou meniť nastavenia, ovládať, upravovať atď. (bez možnosti zmeny hodín, odborov, učiteľov, ...);

V prípade zistenia potreby menšej (do 10%) zmeny zdrojových údajov (zistené chyby, náhle doplnenia) je možné za malý poplatok doobjednať modul generovania rozvrhu;

Kedykoľvek môžete prejsť na štandardnú verziu;

Metodista - štandard.

Okrem funkcií virtuálnej verzie obsahuje:

Modul automatického plánovania;

Rozloženie a kontrola vyučovacej záťaže;

Dôsledné dodržiavanie postupnosti disciplíny (prednášky - 2 hodiny, praktická - 4 hodiny, laboratórium...);

Vytvorenie rozvrhu pre akýkoľvek typ vzdelávacej inštitúcie: týždenný alebo semester (od 1 do 23 týždňov);

Účtovanie spájania skupín (tried) do prúdov a/alebo ich rozdeľovania do podskupín;

Pridelenie odborných učební (počítačové triedy, jazykové laboratóriá, bazén, ...);

Účtovanie pracovného pomeru učiteľov a tried (skrátený úväzok, využívanie spoločnej vzdelávacej základne);

Účtovanie doby prechodu medzi budovami;

Víkendy a sviatky – všeobecné a pre jednotlivé študijné skupiny (štátne, cirkevné, štátne sviatky);

Uvedenie dôvodov „neúspešného priradenia“ tried (učebňa je vyťažená, učiteľ je zaradený na nežiaduci deň v týždni) s možnosťou ich „manuálnej“ opravy;

Možnosť opakovaného automatického „vylepšenia“ harmonogramu;

Možnosť zmeny významu faktorov zohľadnených pri zostavovaní harmonogramu;

Možnosť zavedenia priorít učiteľov - miera zohľadnenia ich individuálnych želaní;

Obmedzenia funkcie „Metodista“:

Viaczmenné rozvrhy sú obmedzené na maximálny počet vyučovacích hodín za deň – 7;

Vyučovanie začína vždy prvou hodinou/dvojicou (v prípade potreby je možné prvej dvojici prideliť „hodinu zadarmo“);

Čas zmeny sa neberie do úvahy (napríklad pre kontrolu možnosti pohybu medzi budovami);

„Úroveň obtiažnosti“ tried sa neberie do úvahy pri ich racionálnom rozložení počas týždňa (aj keď je to možné urobiť nepriamo);

Trvanie vyučovania je konštantné (nie je možné vytvoriť rozvrh na 30-minútovú lekciu na strednej škole a 45-minútovú lekciu na strednej škole).

Príloha 2. Výpis softvérového modulu metód na riešenie problému automatického plánovania

type MyArray= pole poľa real;

MyArray_X = pole longintu;

procedure Step_Dual_simplex(var a:MyArray; m,n,i1,j1:integer);

(vykonáva jeden krok duálnej simplexovej metódy,

vedúci prvok - a)

var i,j:integer;

b,b1:pole skutočných;

SetLength(b,m);Setlength(b1,n);

pre i:=0 až m-1 do b[i]:=a;

pre i:=0 až n-1 do b1[i]:=a;

pre i:=0 až m-1 do

pre j:=0 až n-1 začínajú

ak (i=i1) a (j=j1), potom a:=l/b

ak (i=i1) potom a:=b1[j]/b

if (j=j1) potom a:=-b[i]/b

inak a:=a-b[i]*b1[j]/b;

pre i:=0 až n-1 urob a:=0;a:=-1;

Finalize(b);Finalize(b1);

function Lexikogr_few(a:MyArray; m,n:integer;i,i1:integer):boolean;

(prvý stĺpec je lexikograficky menší ako druhý)

Lexikogr_few:=false;

zatiaľ čo (a=a) a (j

function Find_nu(a:MyArray;m,n:integer; i,i1:integer):longint;

(i je index lexikograficky minimálneho stĺpca)

zatiaľ čo (a=a) a (j

if (j 0) then Find_nu:=Round(Int(a/a));

procedure Full_Integer_Simplex(var x:MyArray_X; a:MyArray; m,n:integer);

(Plne celočíselný algoritmus pre lineárny celočíselný problém

programovanie,

pozri Hu T. "Celočíselné programovanie a toky v sieťach", s. 300-309,

a je matica veľkosti m+n+2*n+1, analogicky:

Musíme nájsť maximum

z= - 10x1 - 14x2 - 21x3

2x1 + 2x2 + 7x3 >= 14

8x1 + 11x2 + 9x3 >= 12

9x1 + 6x2 + 3x3 >=10,

procedúra vráti vektor X, ktorého prvých m komponentov je požadované riešenie,

ak je posledná zložka vektora = 1, riešenie neexistuje alebo je = nekonečno)

var i,i1:integer;

zatiaľ čo (i = 0) do Inc(i); (výrobný reťazec)

zatiaľ čo (j = 0) do Inc(j);

pre i1:=1 až n-1 urob, ak (a

minimálny stĺpec)

(výber alfa)

(Writeln(i," ",j);readln;)

pre i1:=1 až n-1 urobte, ak a

j1:=Find_nu(a,m,n,j,i1);

if (j1>0) a (-a/j1>alfa) potom alfa:=-a/j1;

(writeln(alfa," ",i," ",j);readln;)

(prijatie Gomoriho strihu)

pre i1:=0 až n-1 urobte, ak a>0, potom a:=okrúhle(Int(a/alfa))

a:=round(Int(a/alfa));

ak Frac(a/alfa)0 potom a:=a-1;

Step_Dual_simplex(a,m,n,m-1,j);

kým (i>=m-1) alebo (j>=n);

pre i:=0 až m-1 do x[i]:=kruh(a);

ak j>=n, potom x:=1 inak x:=0;

procedure Step_One_Simplex(var a:MyArray; m,n,i:integer);

var i1,i2:integer;

(Jeden krok priamej celočíselnej metódy (vyrábajúci riadok je posledný

i - generovanie stĺpca))

pre i1:=0 až m-2 urob a:=a/(-a);

pre i2:=0 až n-1 do

pre i1:=0 až m-2 do

ak i2i potom a:=a+a*a;

procedure Direct_Integer_Simplex(var x:MyArray_X; a:MyArray; m,n:integer);

(Priamy celočíselný algoritmus pre problém celočíselného lineárneho programovania,

pozri Hu T. "Celočíselné programovanie a toky v sieťach", s. 344-370,

a je matica veľkosti m+n+3*n+1 analogicky:

je potrebné maximalizovať

z = x1 + x2 + x3

4x1 + 5x2 + 2x3

potom matica a bude vyzerať takto:

10 1 1 1 – prvé číslo v tomto riadku predstavuje hrubý maximálny súčet nezákladných premenných

0 0 0 0 - struna na odrezanie Gomori,

Algoritmus funguje iba vtedy, keď a>=0

vráti vektor X - namiesto matice identity požadované riešenie,

ak posledná zložka obsahuje jednotku, vo výpočtoch je chyba)

var i,j,i1,j1:integer;

b, b1, b2: pole bajtov;

NastavenaDlzka(b,m);NastavenaDlzka(b1,m);

pre i:=0 až m-1 do b1[i]:=0;

(kontrola stavu optimality)

pre j:=1 až n-1 urobte, ak a

zatiaľ čo bool začať

(vyhľadajte stĺpec na generovanie)

bool:=false;j1:=0;

pre j:=1 až n-1 začínajú

ak a>0 potom

pre i:=0 až m-3 urob a:=a/a;

ak nie bool, potom začni j1:=j;bool:=true;koniec else if Lexikogr_few(a,m,n,j,j1)

(hľadajte generujúci reťazec)

pre j:=1 až n-1 do

ak a>0 potom

pre i:=0 až m-3 urob a:=a*a;

Zavládlo ticho, ktoré prelomil sám Švejk s povzdychom:
- ... Vo vojenskej službe musí byť disciplína - bez nej by nikto pre vec nepohol ani prstom. Náš hlavný poručík Makovets vždy hovoril: „Disciplína, idioti, je potrebná. Bez disciplíny by ste liezli po stromoch ako opice. Vojenská služba z vás urobí ľudí, bezmozgových hlupákov!“ No nie je to tak? Predstavte si námestie povedzme na Karlovom námestí a na každom strome sedí jeden vojak bez akejkoľvek disciplíny. Toto ma strašne desí.
Jaroslav HAŠEK DOBRODRUŽSTVÁ DOBRÉHO VOJAKA SCHWEIKA

Rozvrh triedy je kombináciou v priestore a čase disciplíny (predmetu), učiteľa (učiteľov), publika a skupiny (podskupiny, prúdu) študentov.

Formulácia problému

Budem stručný.

• Pri vedení hodiny môžu chýbať účastníci, napríklad na schôdzi katedry, študenti spravidla neprídu alebo študenti odišli na vojenskú katedru (majú vlastný rozvrh) a pre tento typ triede nie je disciplína, učiteľ a obecenstvo.
• Kontinuita (bez okien) je spravidla nevyhnutnou požiadavkou pre študentov a najlepšie pre učiteľov.
• Rozvrh je možné zostaviť na semester/polsemester po týždni, po dvoch týždňoch a čitateľovi/menovateľovi (nepárny/párny týždeň). Existuje aj mesačný harmonogram.
• Triedy by sa mali dať nastaviť v manuálnom režime (inými slovami v editore). Napríklad akademická rada alebo pár veľkého šéfa alebo dokonca povolanie len dobrého človeka.
• Musí existovať systém zákazov pre všetkých účastníkov lekcie. Napríklad teraz takmer všetci učitelia zarábajú bokom (inak nebudete môcť prežiť) alebo triedny fond je rozdelený medzi fakulty a hodiny sa nemôžu konať v časti tried po obede.
• Prítomnosť sofistikovaných želaní učiteľov, jeden dostane 5 hodín denne, aby si uvoľnil ďalšie dni, a druhý nemá viac ako dve hodiny denne, unaví sa a ak je prednáška, tak jedna hodina a určite 2. alebo 3. triede.
• Triedy v rôznych budovách vyžadujú viac času na prechod, ako je čas prestávok medzi triedami. Prirodzená je aj podmienka minimalizácie pohybov.

Záver. Ako vyplýva z vyjadrenia, posúdiť kvalitu harmonogramu je možné až po jeho úplnom zostavení. Preto použitie genetických algoritmov môže umožniť zostaviť riešenie požadovaného problému a dokonca získať v istom zmysle jedno z dobrých. Genetické algoritmy sa zároveň na začiatku veľmi rýchlo zbiehajú k optimálnemu, čo znamená, že množstvo vstupných dát nebude prakticky nijako obmedzené.

Obrázok je prevzatý odtiaľto.

Genetický algoritmus

Čisto rétoricky zopakujem hlavné fázy genetického algoritmu:

1. Nastavte cieľovú funkciu (fitness) pre jednotlivcov v populácii
2. Vytvorte počiatočnú populáciu
3. (Začiatok cyklu)
   1. Rozmnožovanie (kríženie)
   2. Mutácia
   3. Vypočítajte hodnotu účelovej funkcie pre všetkých jednotlivcov
   4. Vznik novej generácie (výber)
   5. Ak sú splnené podmienky zastavenia, potom koniec cyklu, inak (začiatok cyklu).

Najčastejšou chybou pri používaní genetických algoritmov je výber génov. Často sú zvolené gény jednoducho samotným riešením. Výber génov je najnetriviálnejším a najkreatívnejším prvkom pri vytváraní genetického algoritmu. Osobne sa domnievam, že výber génov by mal spĺňať nasledujúce dve základné požiadavky.

1. Na základe sady génov by malo byť rýchlo a jednoznačne skonštruované riešenie požadovaného problému.
2. Pri krížení musí potomok zdediť vlastnosti rodičov.

Komentár. Súbor génov by mal poskytnúť celý súbor (možno optimálnych) riešení problému. V zásade nie je potrebné vyžadovať jeden k jednému, stačí, aby bolo mapovanie génov do priestoru riešenia na(odmietnutie).

Algoritmus plánovania

Popíšem len samotné gény, algoritmus na zostavenie riešenia na ich základe, kríženie a mutáciu.

Ako skúsený dispečer robí rozvrh. Slovo skúsený znamená, že dispečer už raz zostavil grafikon a pozná jeho úzke miesta. Napríklad nedostatok veľkého streamovacieho publika alebo počítačových tried. Prvý kurz, keďže majú veľa streamovaných prednášok a súčasne hodiny v podskupinách na počítačových triedach, angličtina/angličtina od nuly/nemčina/francúzština atď., a úrady vyžadujú, aby prvý kurz v žiadnom prípade nemal okná a žiadne viac ako dve prednášky za deň a dni boli rovnomerne zaťažené. Skúsený dispečer preto zariaďuje prvé „úzke hodiny“, hodiny úradov na ich žiadosť a hodiny obzvlášť otravných učiteľov. Potom pomocou usporiadaných tried ako kostry rýchlo dokončí rozvrh. Skúsme tento proces v istom zmysle napodobniť.

Niektoré hodiny sú už v našom rozvrhu, ostatné budú očíslované postupne. Pole čísel povolaní budeme považovať za genóm, aj keď v zásade je dôležité len poradie povolaní. Aby sme zostavili rozvrh, postupne vytiahneme čísla tried a zaradíme vybranú triedu do rozvrhu, čím sa uspokoja potrebné požiadavky a maximalizuje sa objektívna funkcia pre študentov, učiteľov a publikum (tiež majú kritériá zamestnania).
Ak nie je možné splniť potrebné požiadavky, jedinec s takýmto genómom môže byť vyradený ako neživotaschopný. Ak nie je možné vytvoriť rozvrh, môžete potrebné požiadavky nahradiť pokutou v objektívnej funkcii.

Križovanie môže byť organizované niekoľkými spôsobmi. Napríklad jeden z nich. Majme nasledujúce gény

3 1 2 5 6 4 7
2 3 5 7 1 4 6

Tu môžete vidieť, že aktivita 3 sa vyskytuje v oboch génoch až po pozíciu 2 vrátane a napríklad od pozície 2 po pozíciu 5 je interval pre 1 aktivitu. Urobme nasledujúci znak

_ * * * * _ _ za 1 lekciu
* * * _ _ _ _ pre lekciu 2
* * _ _ _ _ _ pre lekciu 3
_ _ _ _ _ * _ na lekciu 4
_ _ * * _ _ _ pre lekciu 5
_ _ _ _ * * * pre lekciu 6
_ _ _ * * * * pre lekciu 7

tu hviezdičky označujú možné pozície pre čísla povolaní potomka. Ako dieťa alebo deti týchto rodičov si môžete vybrať z jedného alebo viacerých možných riešení. Vždy existuje riešenie, ako vybrať gény potomka, vyhovujú mu napríklad aj samotní obaja rodičia. Prepíšme tabuľku cez množiny možných pozícií

1 pozícia (2, 3)
2. miesto (1, 2, 3)
3. miesto (1, 2, 5)
4. pozícia (1, 5, 7)
5 pozície (1, 6, 7)
6. miesto (4, 6, 7)
Pozícia 7 (6, 7)

Na zostavenie riešení môžete použiť nasledujúci algoritmus. Najprv dáme tie počty tried, ktoré sú menej bežné. Ak ich zoradíme vzostupne, budeme mať
1 krát 4
2 krát 3.5
3 krát 2, 6
4 krát 1, 7
Preto najprv dáme lekciu 4 na 6. pozíciu, potom 3 alebo 5 na pozície (1, 2) alebo (3, 4). Na každom kroku môžete hodiť škatuľku zápaliek. V dôsledku toho môžete získať napríklad nasledujúce kroky pre algoritmus kríženia

* * * * * 4 *
3 * * * * 4 *
3 * * 5 * 4 *
3 * * 5 * 4 6
3 * 2 5 * 4 6
3 * 2 5 7 4 6
3 1 2 5 7 4 6

Keďže je možné, že sa nepodarí zostrojiť správnu postupnosť, je lepšie organizovať algoritmus vo forme jednoduchej rekurzie, aby bolo možné algoritmus zopakovať, t.j. organizovanie nejakého vyhľadávania.

Mutáciu je možné zorganizovať celkom jednoducho náhodným preskupením čísel obsadenia.

Záver

Toto je v istom zmysle pokračovanie mojich príspevkov Program rozvrhu hodín na univerzite a Výpočet úväzku pre katedru.

Opäť navrhujem nasledovné riešenie (náčrt).

• GUI na PyQt alebo PySide
• PosgreSQL DBMS (tu mám pripravených cca 80%), okrem samotného rozvrhu obsahuje aj aplikácie a náplne učiteľov, osnovy a mnoho iného (pre tento účel zverejním jednu alebo viac tém)
• webové rozhranie na CherryPy+Cheetah (ale o tom sa dá diskutovať)
• export akýchkoľvek správ (rozvrhov, kartičiek na školenia atď.) vo formáte OpenDocument (GOST R ISO/IEC 26300-2010. Gosstandart Ruska (06.01.2011)) cez ODFPY
• plánovacie algoritmy odo mňa (o tom je táto téma)
• výroba odo mňa
• pre záujemcov práca na spoločnom jadre
• pre záujemcov adaptácia na vlastnú univerzitu a možnosť všetko flexibilne meniť, život ide ďalej a úradníci nespia

Ďakujem všetkým, ktorí sa ozvali, po diskusii na túto tému sa bude dať zorganizovať.