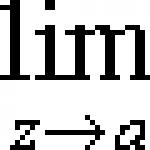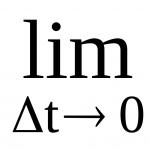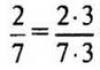V mnohých oblastiach matematiky je potrebné dokázať pravdivosť výroku, ktorý závisí od , t.j. pravdivosť návrhu p(n) pre " nнN (pre akékoľvek n ON p(n) správny).
Často sa to dá dokázať metóda matematickej indukcie.
Táto metóda je založená na princípe matematickej indukcie. Zvyčajne sa vyberá ako jedna z axióm aritmetiky, a preto sa prijíma bez dôkazu. Podľa princípu matematickej indukcie je veta p(n) sa považuje za pravdivé pre všetky prirodzené hodnoty premennej, ak sú splnené dve podmienky:
1. Ponuka p(n) pravda pre n= 1.
2. Z vety, že p(n) pravda pre n =k (k -ľubovoľné prirodzené číslo) z toho vyplýva, že platí pre n =k+ 1.
Metódou matematickej indukcie sa rozumie nasledujúca metóda dôkazu
1. Skontrolujte pravdivosť tvrdenia n= 1 je základ indukcie.
2. Predpokladajme, že tvrdenie je pravdivé pre n = k - indukčný predpoklad.
3. Dokážte, že potom platí aj pre n =k+ 1 indukčný prechod.
Niekedy návrh p(n) Ukazuje sa, že nie pre všetky prirodzené n, a počnúc od niektorých pre n = n 0. V tomto prípade sa pravdivosť kontroluje v indukčnej základni p(n) pri n = n 0.
Príklad 1 Nechaj . Dokáž to
1. Indukčná základňa: kedy n= 1 podľa definície S 1 = 1 a podľa vzorca dostaneme jeden výsledok. Výrok je správny.
n=k a .
n=k+ 1. Dokážme, že .
Skutočne, podľa indukčného predpokladu
Transformujme tento výraz
Indukčný prechod je dokázaný.
Komentujte. Je užitočné zapísať si, čo je dané (induktívny predpoklad) a čo treba dokázať!
Príklad 2 dokázať
1. Základ indukcie. o n= 1, tvrdenie je zjavne pravdivé.
2. Indukčný predpoklad. Nechaj n=k a
3. Indukčný prechod. Nechaj n=k+ 1. Dokážme:
Skutočne, odmocnime pravú stranu ako súčet dvoch čísel:
Použitím induktívneho predpokladu a vzorca pre súčet aritmetickej progresie: dostaneme
Príklad 3 Dokážte nerovnosť
1. Základom indukcie je v tomto prípade overenie pravdivosti tvrdenia pre , t.j. treba kontrolovať nerovnosť. Na to stačí odmocniť nerovnosť: alebo 63< 64 – неравенство верно.
2. Nerovnosť nech platí pre , t.j.
3. Dokážte:
Používame indukčnú hypotézu
Keďže vieme, ako má vyzerať pravá strana v dokazovanej nerovnosti, vyberieme túto časť
Zostáva potvrdiť, že dodatočný faktor nepresahuje jednotu. naozaj,
Príklad 4 Dokážte, že každé prirodzené číslo končí číslicou.
1. Najmenšie prirodzené číslo, od ktorého je výrok pravdivý, sa rovná . .
2. Nechajte číslo pre končiť na . To znamená, že toto číslo možno zapísať ako , kde je nejaké prirodzené číslo. Potom .
3. Nechajte . Dokážme, že to končí v . Pomocou výslednej reprezentácie dostaneme
Posledné číslo má presne jedničky.
Dodatok
1.4. Metóda matematickej indukcie
Ako viete, matematické tvrdenia (vety) musia byť podložené, dokázané. Teraz sa zoznámime s jednou z metód dôkazu – metódou matematickej indukcie.
V širšom zmysle je indukcia spôsob uvažovania, ktorý vám umožňuje prejsť od konkrétnych tvrdení k všeobecným. Spätný prechod od všeobecných tvrdení ku konkrétnym sa nazýva dedukcia.
Dedukcia vždy vedie k správnym záverom. Poznáme napríklad všeobecný výsledok: všetky celé čísla končiace nulou sú deliteľné číslom 5. Z toho, samozrejme, môžeme usudzovať, že každé konkrétne číslo končiace na 0, napríklad 180, je deliteľné číslom 5.
Súčasne môže indukcia viesť k nesprávnym záverom. Ak si napríklad všimneme, že číslo 60 je deliteľné číslami 1, 2, 3, 4, 5, 6, nemáme právo dospieť k záveru, že 60 je deliteľné akýmkoľvek číslom.
Metóda matematickej indukcie umožňuje v mnohých prípadoch rigorózne dokázať platnosť všeobecného tvrdenia P(n), ktorého formulácia obsahuje prirodzené číslo n.
Aplikácia metódy zahŕňa 3 etapy.
1) Základ indukcie: overíme platnosť výroku P(n) pre n = 1 (alebo pre inú, súkromnú hodnotu n, z ktorej sa predpokladá platnosť P(n)).
2) Predpoklad indukcie: predpokladáme, že P(n) platí pre n = k.
3) Krok indukcie: pomocou predpokladu dokážeme, že P(n) platí pre n = k + 1.
Výsledkom je, že P(n) platí pre ľubovoľné n ∈ N. Vskutku, pre n = 1 je tvrdenie pravdivé (základ indukcie). A preto to platí aj pre n = 2, keďže prechod z n = 1 na n = 2 je opodstatnený (indukčný krok). Opakovaným aplikovaním kroku indukcie získame platnosť P(n) pre n = 3, 4, 5, . . ., teda platnosť P(n) pre všetky n.
Príklad 14. Súčet prvých n nepárnych prirodzených čísel je n2: 1 + 3 + 5 + ...
+ (2n - 1) = n2.
Dôkaz bude vykonaný metódou matematickej indukcie.
1) Základ: pre n=1 je vľavo iba jeden člen, dostaneme: 1 = 1.
Výrok je správny.
2) Predpoklad: predpokladáme, že pre nejaké k platí rovnosť: 1 + 3 + 5 + ... + (2k - 1) = k2.
Riešenie problémov o pravdepodobnosti zásahov počas výstrelov
Všeobecné vyjadrenie problému je nasledovné:
Pravdepodobnosť zasiahnutia cieľa jednou ranou sa rovná $p$. $n$ výstrelov. Nájdite pravdepodobnosť, že cieľ bude zasiahnutý presne $k$ krát (zásahov bude $k$).
Aplikujeme Bernoulliho vzorec a dostaneme:
$$ P_n(k)=C_n^k \cdot p^k \cdot (1-p)^(n-k) = C_n^k \cdot p^k \cdot q^(n-k).
Tu $C_n^k$ predstavuje počet kombinácií od $n$ do $k$.
Ak problém zahŕňa niekoľko šípok s rôzne pravdepodobnosti zasiahnutie cieľa, teóriu, príklady riešení a kalkulačku nájdete tu.
Video tutoriál a šablóna programu Excel
Pozrite si naše video o riešení problémov s Bernoulliho výstrelmi a naučte sa, ako používať Excel na riešenie bežných problémov.
Výpočtový súbor programu Excel z videa si môžete zadarmo stiahnuť a použiť na riešenie vašich problémov.
Príklady riešenia problémov pri zasiahnutí cieľa v sérii výstrelov
Pozrime sa na niekoľko typických príkladov.
Príklad 1 Vystrelilo 7 rán. Pravdepodobnosť zásahu jednou ranou je 0,705. Nájdite pravdepodobnosť, že bude presne 5 zásahov.
Dostaneme, že problém sa týka opakovaných nezávislých testov (výstrely na cieľ), celkovo sa vypáli $n=7$ výstrelov, pravdepodobnosť zásahu pri každom $p=0,705$, pravdepodobnosť chýbania $q=1-p =1-0,705 = 0,295 $.
Musíme zistiť, že bude presne $k=5$ zásahov. Všetko dosadíme do vzorca (1) a dostaneme: $$ P_7(5)=C_(7)^5 \cdot 0,705^5 \cdot 0,295^2 = 21\cdot 0,705^5 \cdot 0,295^2= 0,318. $$
Príklad 2 Pravdepodobnosť zasiahnutia cieľa jednou ranou je 0,4.
Na cieľ sa strieľajú štyri nezávislé výstrely. Nájdite pravdepodobnosť, že cieľ bude zasiahnutý aspoň jedným zásahom.
Preštudujeme si problém a zapíšeme si parametre: $n=4$ (výstrel), $p=0,4$ (pravdepodobnosť zásahu), $k \ge 1$ (aspoň jeden zásah bude).
Používame vzorec pre pravdepodobnosť opačnej udalosti (nedošlo k žiadnemu zásahu):
$$ P_4(k \ge 1) = 1-P_4(k \lt 1) = 1-P_4(0)= $$ $$ =1-C_(4)^0 \cdot 0,4^0 \cdot 0 ,6 ^ 4 = 1 - 0,6 ^ 4 = 1 - 0,13 = 0,87. $$
Pravdepodobnosť zásahu aspoň raz zo štyroch je 0,87 alebo 87 %.
Príklad 3 Pravdepodobnosť zasiahnutia cieľa strelcom je 0,3.
Nájdite pravdepodobnosť, že pri 6 výstreloch bude cieľ zasiahnutý tri až šesťkrát.
Na rozdiel od predchádzajúcich problémov tu musíte nájsť pravdepodobnosť, že počet zásahov bude v určitom intervale (a nie presne rovný nejakému číslu). Ale vzorec je rovnaký.
Nájdite pravdepodobnosť, že cieľ bude zasiahnutý trikrát až šesťkrát, to znamená, že to bude buď 3, alebo 4, alebo 5 alebo 6 zásahov.
Tieto pravdepodobnosti sa vypočítavajú podľa vzorca (1):
$$ P_6(3)=C_(6)^3 \cdot 0,3^3\cdot 0,7^3 = 0,185. $$ $$ P_6(4)=C_(6)^4 \cdot 0,3^4\cdot 0,7^2 = 0,06. $$ $$ P_6(5)=C_(6)^5 \cdot 0,3^5\cdot 0,7^1 = 0,01. $$ $$ P_6(6)=C_(6)^6 \cdot 0,3^6\cdot 0,7^0 = 0,001.
Keďže udalosti sú nekompatibilné, požadovanú pravdepodobnosť možno nájsť pomocou vzorca na sčítanie pravdepodobností: $$ P_6(3 \le k \le 6)=P_6(3)+P_6(4)+P_6(5)+P_6(6) =$$ $$ = 0,185 + 0,06 + 0,01 + 0,001 = 0,256, $ $
Príklad 4 Pravdepodobnosť aspoň jedného zásahu do terča štyrmi ranami je 0,9984. Nájdite pravdepodobnosť zasiahnutia cieľa jednou ranou.
Označme pravdepodobnosť zasiahnutia cieľa jednou ranou. Zadáme udalosť:
$A = $ (Zo štyroch výstrelov aspoň jedna zasiahne cieľ),
ako aj jeho opačnú udalosť, ktorú možno napísať ako:
$\overline(A) = $ (Všetky 4 výstrely minuli cieľ, žiadne zásahy).
Zapíšme si vzorec pre pravdepodobnosť udalosti $A$.
Zapíšme si známe hodnoty: $n=4$, $P(A)=0,9984$. Dosaďte do vzorca (1) a získajte:
$$ P(A)=1-P(\overline(A))=1-P_4(0)=1-C_(4)^0 \cdot p^0 \cdot (1-p)^4=1- (1-p)^4=0,9984.
Vyriešime výslednú rovnicu:
$$ 1-(1-p)^4=0,9984,\\ (1-p)^4=0,0016,\\ 1-p=0,2,\\ p=0,8. $$
Pravdepodobnosť zasiahnutia cieľa jednou ranou je teda 0,8.
Ďakujem za prečítanie a zdieľanie s ostatnými
užitočné odkazy
Nájdite v riešení hotové úlohy:
Online výpočty pomocou Bernoulliho vzorca
Riešenie nerovnosti pomocou kalkulačky
Nerovnosť v matematike platí pre všetky rovnice, kde "=" je nahradené ktorýmkoľvek z nasledujúcich znakov: \ [> \] \ [\geq \] \ [
* lineárne;
* námestie;
* zlomkové;
* orientačné;
* trigonometrické;
* logaritmické.
V závislosti od toho sa nerovnosti nazývajú lineárne, čiastočné atď.
Mali by ste si byť vedomí týchto príznakov:
* nerovnosti väčšie ako (>) alebo menšie ako (
* Nerovnosti s ikonami, ktoré sú väčšie alebo rovné \[\geq\] menšie alebo rovné [\leq\], sa nazývajú neprofesionálne;
* ikona nie je rovnaká \[\ne\] samotná, ale prípady s touto ikonou je potrebné neustále riešiť.
Takáto nerovnosť sa rieši transformáciami identít.
Prečítajte si aj náš článok „Vyriešte kompletné riešenie pre online rovnicu“
Predpokladajme, že platí nasledujúca nerovnosť:
Riešime to rovnako ako lineárnu rovnicu, no mali by sme pozorne sledovať znamienko nerovnosti.
Najprv presunieme pojmy z neznámeho doľava, zo známeho doprava, pričom obrátime symboly:
Potom obe strany vydelíme -4 a otočíme znamienko nerovnosti:
Toto je odpoveď na túto rovnicu.
Kde môžem vyriešiť nerovnosť na internete?
Rovnicu môžete vyriešiť na našej webovej stránke pocketteacher.ru.
Bernoulliho kalkulačka nerovnosti
Bezplatné online záchranné riešenie v priebehu niekoľkých sekúnd vyrieši online rovnicu akejkoľvek zložitosti. Jediné, čo musíte urobiť, je zadať svoje údaje do záchrany. Na našej stránke si môžete pozrieť aj video návod a naučiť sa riešiť rovnicu.
A ak máte otázky, môžete sa ich opýtať v našej skupine Vkontakte: pocketteacher. Pridajte sa do našej skupiny, radi vám pomôžeme.
Úplná matematická indukčná metóda
Riešenie rovníc / diferenciálne rovnice
© RU test - online kalkulačky
Riešenie diferenciálnych rovníc
Zadajte rozdiel. rovnica:
Pomocou kalkulačky môžete riešiť diferenciálne rovnice rôznej zložitosti.
Príklady vyriešených diferenciálnych rovníc
Ministerstvo školstva Saratovského regiónu
Štátna sociálno-ekonomická univerzita v Saratove
Krajská súťaž matematických a počítačových prác školákov
"Vektor budúcnosti - 2007"
„Metóda matematickej indukcie.
Jeho aplikácia na riešenie algebraických problémov“
(časť "matematika")
tvorivá práca
10 žiakov „A“ triedy
MOU "Gymnázium č. 1"
Oktyabrsky okres Saratov
Harutyunyan Gayane.
Vedúci práce:
učiteľ matematiky
Grishina Irina Vladimirovna
Saratov
2007
Úvod ……………………………………………………………………………………………… 3
Princíp matematickej indukcie a jeho
dôkaz ……………………………………………………………………………….. 4
Príklady riešenia problémov………………………………………………………………………..9
Záver……………………………………………………………………………………….. 16
Literatúra……………………………………………………………………………………………… 17
Úvod.
Metódu matematickej indukcie možno porovnať s pokrokom. Začíname od najnižšieho, výsledkom logického myslenia sa dostávame k najvyššiemu. Človek sa vždy snažil o pokrok, o schopnosť logicky rozvíjať svoje myslenie, čo znamená, že samotná príroda mu predurčila myslieť induktívne a svoje myslenie podopierať dôkazmi vykonávanými podľa všetkých pravidiel logiky.
V súčasnosti sa oblasť použitia metódy matematickej indukcie rozrástla, no v školských osnovách sa jej, žiaľ, venuje málo času. Ale toto je také dôležité – vedieť myslieť induktívne.
Princíp matematickej indukcie a jej dôkaz
Vráťme sa k podstate metódy matematickej indukcie. Uvažujme o rôznych vyhláseniach. Dajú sa rozdeliť na všeobecné a konkrétne.Uveďme príklady všeobecných tvrdení.
Všetci občania Ruska majú právo na vzdelanie.
V každom rovnobežníku sú uhlopriečky v priesečníku rozdelené na polovicu.
Všetky čísla končiace nulou sú deliteľné 5.
Relevantné príklady súkromných vyhlásení:
Petrov má právo na vzdelanie.
V rovnobežníku ABCD sú uhlopriečky v priesečníku rozdelené na polovicu.
140 je deliteľné 5.
Prechod od všeobecných tvrdení ku konkrétnym sa nazýva dedukcia (z lat odpočet - záver podľa pravidiel logiky).
Uvažujme o príklade deduktívnej dedukcie.
Všetci občania Ruska majú právo na vzdelanie. (jeden)
Petrov je občanom Ruska. (2)
Petrov má právo na vzdelanie. (3)
Zo všeobecného tvrdenia (1) sa pomocou (2) získa konkrétne tvrdenie (3).
Obrátený prechod od konkrétnych výrokov k všeobecným výrokom sa nazýva indukcia (z lat indukcia - vedenie).
Indukcia môže viesť k správnym aj nesprávnym záverom.
Vysvetlime si to na dvoch príkladoch.
140 je deliteľné 5. (1)
Všetky čísla končiace nulou sú deliteľné 5. (2)
140 je deliteľné 5. (1)
Všetky trojciferné čísla sú deliteľné 5. (2)
Z konkrétneho výroku (1) sa získa všeobecný výrok (2). Vyhlásenie (2) je pravdivé.
Druhý príklad ukazuje, ako je možné získať všeobecný výrok (3) z konkrétneho výroku (1), navyše výrok (3) nie je pravdivý.
Položme si otázku, ako využiť indukciu v matematike, aby sme získali len správne závery. Zoberme si niekoľko príkladov indukcie, ktorá je v matematike neprijateľná.
Príklad 1.
Uvažujme štvorcovú trojčlenku nasledujúceho tvaru Р(x)= x 2 + x + 41, ktorej venoval pozornosť Leonard Euler.
P(0) = 41, P(1) = 43, P(2) = 47, P(3) = 53, P(4) = 61, P(5) = 71, P(6) = 83, P (7) = 97, P(8) = 113, P(9) = 131, P(10) = 151.
Vidíme, že zakaždým, keď je hodnota trojčlenky prvočíslo. Na základe získaných výsledkov tvrdíme, že pri dosadzovaní do uvažovaného trojčlenu namiesto x Akékoľvek nezáporné celé číslo má vždy za následok prvočíslo.
Vyvodený záver však nemožno považovať za spoľahlivý. Čo sa deje? Faktom je, že v odôvodnení sa všeobecné tvrdenia o akomkoľvek x uvádzajú iba na základe toho, že sa toto tvrdenie ukázalo ako pravdivé pre niektoré hodnoty x.
Pri bližšom skúmaní trinomu P(x) sú čísla P(0), P(1), ..., P(39) prvočísla, ale P(40) = 41 2 je zložené číslo. A celkom jasne: P(41) = 41 2 +41+41 je násobok 41.
V tomto príklade sme sa stretli s tvrdením, ktoré je pravdivé v 40 špeciálnych prípadoch a napriek tomu sa vo všeobecnosti ukázalo ako nespravodlivé.
Pozrime sa na niekoľko ďalších príkladov.
Príklad 2
V 17. storočí V.G. Leibniz dokázal, že pre každé prirodzené n sú čísla tvaru n 3 - n násobky 3, n 5 - n sú násobky 5, n 7 - n sú násobky 7. Na základe toho navrhol, že pre ľubovoľné nepárne k a prirodzené n, číslo nk - n násobok k, ale čoskoro si sám všimol, že 2 9 -2 = 510, čo, samozrejme, nie je deliteľné 9.
Uvažované príklady nám umožňujú vyvodiť dôležitý záver: vyhlásenie môže byť pravdivé v mnohých špeciálnych prípadoch a zároveň nespravodlivé vo všeobecnosti.
Prirodzene vyvstáva otázka: existuje tvrdenie, ktoré je pravdivé v niekoľkých špeciálnych prípadoch; nie je možné zvážiť všetky špeciálne prípady; ako vieš, či je toto tvrdenie vôbec pravdivé?
Túto otázku možno niekedy vyriešiť použitím špeciálnej metódy uvažovania nazývanej metóda matematickej indukcie. Táto metóda je založená na princíp matematickej indukcie, uzavretá takto: tvrdenie je pravdivé pre každé prirodzené n, ak:
platí pre n = 1;
z platnosti tvrdenia pre nejaké ľubovoľné prirodzené n =k vyplýva, že platí pre n = k +1.
Dôkaz.
Predpokladajme opak, teda nech platí tvrdenie nie pre každé prirodzené n. Potom existuje prirodzené číslo m také, že
tvrdenie pre n = m nie je pravdivé,
pre všetky n
Je zrejmé, že m >1, keďže tvrdenie platí pre n =1 (podmienka 1). Preto je m -1 prirodzené číslo. Pre prirodzené číslo m -1 je tvrdenie pravdivé, ale pre ďalšie prirodzené číslo m neplatí. To je v rozpore s podmienkou 2. Výsledný rozpor ukazuje, že predpoklad je nesprávny. Preto tvrdenie platí pre akékoľvek prirodzené n, h.e.d.
Dôkaz založený na princípe matematickej indukcie sa nazýva dôkaz metódou matematickej indukcie. Takýto dôkaz by mal pozostávať z dvoch častí, z dôkazu dvoch nezávislých viet.
Veta 1. Výrok platí pre n = 1.
Veta 2. Výrok platí pre n =k +1, ak platí pre n=k, kde k je ľubovoľné prirodzené číslo.
Ak sú obe tieto vety dokázané, potom na základe princípu matematickej indukcie platí tvrdenie pre všetky
prirodzené n .
Treba zdôrazniť, že dôkaz matematickou indukciou si určite vyžaduje dôkaz oboch viet 1 a 2. Zanedbanie vety 2 vedie k nesprávnym záverom (príklady 1-2). Ukážme si na príklade, aký potrebný je dôkaz 1. vety.
Príklad 3. „Veta“: každé prirodzené číslo sa rovná prirodzenému číslu, ktoré za ním nasleduje.
Dôkaz bude vykonaný metódou matematickej indukcie.
Predpokladajme, že k = k +1 (1).
Dokážme, že k +1=k +2 (2). Ak to chcete urobiť, pridajte ku každej časti „rovnosti“ (1) 1. Dostaneme „rovnosť“ (2). Ukazuje sa, že ak je tvrdenie pravdivé pre n =k , potom platí aj pre n =k +1. atď.
Zjavný „dôsledok“ z „vety“: všetky prirodzené čísla sú si rovné.
Chyba spočíva v tom, že veta 1, ktorá je potrebná na uplatnenie princípu matematickej indukcie, nebola dokázaná a nie je pravdivá, ale bola dokázaná iba druhá veta.
Obzvlášť dôležité sú vety 1 a 2.
Veta 1 vytvára základ pre indukciu. Veta 2 dáva právo na neobmedzené automatické rozširovanie tejto základne, právo prejsť z tohto konkrétneho prípadu do ďalšieho, z n na n + 1.
Ak veta 1 nebola dokázaná, ale veta 2 bola dokázaná, potom základ pre vedenie indukcie nebol vytvorený a potom nemá zmysel aplikovať vetu 2, pretože v skutočnosti nie je čo rozširovať. .
Ak veta 2 nebola dokázaná a bola dokázaná iba veta 1, potom aj keď bol vytvorený základ na vedenie indukcie, právo na rozšírenie tohto základu chýba.
Poznámky.
Niekedy je druhá časť dôkazu založená na platnosti tvrdenia nielen pre n =k, ale aj pre n =k -1. V tomto prípade musí byť výrok v prvej časti testovaný na ďalšie dve hodnoty n .
Niekedy sa tvrdenie dokazuje nie pre akékoľvek prirodzené n , ale pre n > m , kde m je nejaké celé číslo. V tomto prípade je v prvej časti dôkazu tvrdenie overené pre n = m +1 a ak je to potrebné, pre niekoľko nasledujúcich hodnôt n.
Ak zhrnieme, čo bolo povedané, máme: metóda matematickej indukcie umožňuje pri hľadaní všeobecného zákona testovať hypotézy, ktoré v tomto prípade vyvstanú, zahodiť nepravdivé a tvrdiť pravdivé.
Každý pozná úlohu procesov zovšeobecňovania výsledkov jednotlivých pozorovaní a experimentov (teda indukcie) pre empirické, experimentálne vedy. Na druhej strane matematika bola dlho považovaná za klasický príklad implementácie čisto deduktívnych metód, pretože sa vždy explicitne alebo implicitne predpokladá, že všetky matematické výroky (okrem tých, ktoré sú akceptované ako počiatočné - axiómy) sú dokázané a špecifické aplikácie z týchto tvrdení sú odvodené z dôkazov vhodných pre všeobecné prípady (dedukcia).
Čo znamená indukcia v matematike? Treba to chápať ako nie celkom spoľahlivú metódu a ako hľadať kritérium spoľahlivosti takýchto indukčných metód? Alebo istota matematických záverov rovnakého charakteru ako experimentálne zovšeobecnenia experimentálnych vied, takže by nebolo zlé „overiť“ akýkoľvek dokázaný fakt? V skutočnosti to tak nie je.
Indukcia (vedenie) na hypotézu hrá v matematike veľmi dôležitú, ale čisto heuristickú úlohu: umožňuje uhádnuť, aké by malo byť riešenie. Ale matematické tvrdenia sú stanovené iba deduktívne. A metóda matematickej indukcie je čisto deduktívna metóda dôkazu. Dôkaz vykonaný touto metódou skutočne pozostáva z dvoch častí:
takzvaný "základ" - deduktívny dôkaz požadovanej vety pre jedno (alebo niekoľko) prirodzených čísel;
induktívny krok spočívajúci v deduktívnom dôkaze všeobecného tvrdenia. Veta je presne dokázaná pre všetky prirodzené čísla. Zo základu dokázaného napríklad pre číslo 0 dostaneme indukčným krokom dôkaz pre číslo 1, potom rovnakým spôsobom pre 2, pre 3 ... - a tak možno tvrdenie odôvodniť pre akékoľvek prirodzené číslo.
Inými slovami, názov „matematická indukcia“ je spôsobený tým, že táto metóda je v našich mysliach jednoducho spojená s tradičným induktívnym uvažovaním (koniec koncov, základ je skutočne dokázaný len pre konkrétny prípad); induktívny krok, na rozdiel od kritérií vierohodnosti induktívneho uvažovania založených na skúsenostiach v prírodných a spoločenských vedách, je všeobecným tvrdením, ktoré nepotrebuje žiadny konkrétny predpoklad a je dokázané podľa prísnych kánonov deduktívneho uvažovania. Preto sa matematická indukcia nazýva „úplná“ alebo „dokonalá“, keďže ide o deduktívnu, úplne spoľahlivú metódu dôkazu.
Príklady riešenia problémov
Indukcia v algebre
Zvážte niekoľko príkladov algebraických problémov, ako aj dôkaz rôznych nerovností, ktoré možno vyriešiť pomocou metódy matematickej indukcie.
Úloha 1. Uhádnite vzorec pre súčet a dokážte ho.
A( n )= 2 1 2 + 3 2 2 + .....+ (n +1) n 2 .
Riešenie.
1. Transformujme výraz pre súčet А(n):
A(n)= 2 1 2 + 3 2 2 + ….+ (n+1) n 2 = (1+1) 1 2 + (2+1) 2 2 + …. + (n+1) n 2 = =1 1 2 + 2 2 2 + …+n n 2 + 1 2 + 2 2 +… +n 2 =1 3 + 2 3 +… +n 3 +1 2 + 2 2 +… +n 2 = В(n) + C(n), kde B(n) = 1 3 + 2 3 + …..+ n 3, C(n)= 1 2 + 2 2 + …+ n 2 .
2. Uvažujme súčty C (n) a B (n).
a) C( n) = 12 + 22 +...+ n2. Jedným z často sa vyskytujúcich problémov metódy matematickej indukcie je dokázať, že pre akékoľvek prirodzené n je rovnosť
1 2 + 2 2 +…+ n 2 = (1)
Predpokladajme, že (1) platí pre všetky n N.
b ) B(n) = 1 3 + 2 3 + …..+ n3. Pozrime sa, ako sa hodnoty B (n) menia v závislosti od n.
B(1) = 13 = 1.
B(2) = 1 3 + 2 3 = 9 = 3 2 = (1 + 2) 2
B(3) = 1 3 + 2 3 + 3 3 = 36 = 
Dá sa teda predpokladať, že
B (n) = (1 + 2 + ….+ n)2 = 
(2)
c) Výsledkom je, že pre súčet А(n) dostaneme
A( n) ==
= (*)
3. Dokážme získaný vzorec (*) metódou matematickej indukcie.
a) skontrolujte rovnosť (*) pre n = 1.
A(1) = 2
=2,
Je zrejmé, že vzorec (*) platí pre n = 1.
b) predpokladajme, že vzorec (*) platí pre n=k , kde k N, teda rovnosť
A(k)= 
Na základe predpokladu dokážeme platnosť vzorca pre n =k +1. naozaj,
A(k+1)=
Keďže vzorec (*) platí pre n =1 a z predpokladu, že platí pre nejaké prirodzené k , vyplýva, že platí pre n =k +1, na základe princípu matematickej indukcie sme dospeli k záveru, že rovnosť
platí pre ľubovoľné prirodzené n .
Úloha 2.
Vypočítajte súčet 1-2 + 3-4 +…(-1) n -1 n .
Riešenie.
Zapíšme si postupne hodnoty súčtov pre rôzne hodnoty n.
A(1)=1, A(2)=1-2= -1, A(3)=1-2+3=2, A(4)=1-2+3-4= -2,
A(5)=1-2+3-4+5=3, A(6)=1-2+3-4+5-6= -3.
Pozorovaním vzoru môžeme predpokladať, že A (n)= - pre párne n a A (n)= 
za nepárne n. Skombinujme oba výsledky do jedného vzorca:
A(n) = 
, kde r je zvyšok po delení n 2.
A r , je samozrejme určené nasledujúcim pravidlom
0 ak n je párne,
r=
1 ak n je nepárne.
Potom r(dá sa uhádnuť) môže byť reprezentované ako: 
Nakoniec dostaneme vzorec pre A (n):
A(n)=
(*)
Dokážme rovnosť (*) pre všetky n N metóda matematickej indukcie.
2. a) Skontrolujte rovnosť (*) pre n =1. A(1) = 1= 
Rovnosť je spravodlivá
b) Predpokladajme, že rovnosť
1-2+3-4+…+(-1) n-1 n= 
pravda pri n=k. Dokážme, že platí aj pre n =k + 1, t.j.
A(k+1)= 
Naozaj,
A(k+1)=A(k)+(-1) k(k+1)= 
=
Q.E.D.
Metóda matematickej indukcie sa využíva aj pri riešení úloh deliteľnosti.
Úloha 3.
Dokážte, že číslo N (n)=n 3 + 5n je deliteľné 6 pre každé prirodzené n.
Dôkaz.
o n = 1 číslo N (1) = 6, a preto je tvrdenie pravdivé.
Nech je číslo N (k )=k 3 +5k pre nejaké prirodzené k deliteľné číslom 6. Dokážme, že N (k +1)= (k +1) 3 + 5(k +1) je deliteľné 6. Naozaj, máme
N(k+1)= (k+1)3+5(k+1)=(k3+5k)+3k (k+1)+6.
Pokiaľ ide o k a k +1 sú susedné prirodzené čísla, potom je jedno z nich nevyhnutne párne, takže výraz 3k (k +1) je deliteľný 6. Dostaneme teda, že N (k +1) je deliteľné aj 6. Výstup číslo N (n)=n 3 + 5n je deliteľné 6 pre ľubovoľné prirodzené n.
Zvážte riešenie zložitejšej úlohy deliteľnosti, keď je potrebné niekoľkokrát použiť metódu úplnej matematickej indukcie.
Úloha 4.
Dokážte, že pre akékoľvek prirodzené n číslo 
nie je deliteľné ani 2 n +3 .
Dôkaz.
Predstavte si vo forme diela =
= (*)
Za predpokladu, že prvý faktor v (*) nie je rovnomerne deliteľný číslom 2 k +3 , teda v zobrazení zloženého čísla 
vo forme súčinu prvočísel sa číslo 2 opakuje najviac (k + 2) krát. Takže dokázať, že číslo 
nie je deliteľné 2 k +4 , musíme to dokázať 
nie je deliteľné 4.
Na dôkaz tohto tvrdenia dokážeme pomocné tvrdenie: pre ľubovoľné prirodzené n nie je číslo 3 2 n +1 deliteľné 4. Pre n =1 je tvrdenie zrejmé, keďže 10 nie je bezo zvyšku deliteľné 4. Za predpokladu, že 3 2 k +1 nie je deliteľné 4, dokážeme, že ani 3 2(k +1) +1 nie je deliteľné
o 4. Predstavme posledný výraz ako súčet:
32(k+1) +1=3 2k+2+1=3 2k*9+1=(32k+1)+8*32k. Druhý člen súčtu je deliteľný 4, ale prvý nie je deliteľný. Preto celý súčet nie je bezo zvyšku deliteľný 4. Pomocné tvrdenie je dokázané.
Teraz je to už jasné nie je deliteľné 4, pretože 2k je párne číslo.
Nakoniec dostaneme to číslo 
nie je rovnomerne deliteľné 2 n + 3 pre žiadne prirodzené n .
Uvažujme teraz o príklade použitia indukcie pri dôkaze nerovností.
Úloha 5.
Pre ktoré prirodzené n platí nerovnosť 2 n > 2n + 1?
Riešenie.
1. Kedy n=121< 2*1+1,
pri n = 2 2 2< 2*2+1,
pri n = 3 2 3 > 2*3+1,
pri n = 424 > 2*4+1.
Zdá sa, že nerovnosť platí pre akékoľvek prirodzené n 3. Dokážme toto tvrdenie.
2. Kedy n =3 platnosť nerovnosti sa už ukázala. Teraz nech platí nerovnosť pre n =k , kde k je nejaké prirodzené číslo nie menšie ako 3, t.j.
2 k > 2k+1 (*)
Dokážme, že potom nerovnosť platí aj pre n =k +1, teda 2 k +1 >2(k +1)+1. Vynásobením (*) 2 dostaneme 2k +1 >4k +2. Porovnajme výrazy 2(k +1)+1 a 4k +2.
4k+2-(2(k+1)+1)=2k-1. Je zrejmé, že 2k -1>0 pre akékoľvek prirodzené k. Potom 4k +2>2(k +1)+1, t.j. 2k+1 >2(k+1)+1. Tvrdenie bolo dokázané.
Úloha 6.
Nerovnosť pre aritmetický priemer a geometrický priemer n nezáporných čísel (Cauchyho nerovnosť)., dostaneme =
Ak aspoň jedno z čísel 
sa rovná nule, potom platí aj nerovnosť (**).
Záver.
Pri práci som študoval podstatu metódy matematickej indukcie a jej dôkaz. V príspevku sú prezentované problémy, v ktorých zohrávala dôležitú úlohu neúplná indukcia vedúca k správnemu riešeniu a následne je vykonaný dôkaz získaný metódou matematickej indukcie.
Literatúra.
Boltyansky V.G., Sidorov Yu.V., Shaburin M.I. Prednášky a úlohy v elementárnej matematike; Veda, 1974.
Vilenkin N.Ya. , Shvartburd S.I. Matematická analýza.-
M.: Vzdelávanie, 1973.
Galitsky M.L., Moshkovich M.M., Shvartburd S.I. Hĺbkové štúdium kurzu algebry a matematickej analýzy - M .: Education, 1990.
Potapov M.K., Aleksandrov V.V., Pasichenko P.I. Algebra a analýza elementárnych funkcií.- M.: Nauka, 1980.
Sominsky I.S., Golovina M.L., Yaglom I.M. O matematickej indukcii - M.: Nauka, 1967.
Dôkazová metóda založená na Peanovej axióme 4 sa používa na dôkaz mnohých matematických vlastností a rôznych tvrdení. Základom toho je nasledujúca veta.
Veta. Ak vyhlásenie A(n) s prirodzenou premenlivosťou n pravda pre n= 1 a z toho, že platí pre n=k, z toho vyplýva, že to platí aj pre ďalšie číslo n=k, potom vyhlásenie A(n) n.
Dôkaz. Označiť podľa M množina tých a len tých prirodzených čísel, pre ktoré výrok A(n) pravda. Potom z podmienky vety máme: 1) 1 M; 2) k MkM. Na základe axiómy 4 sme teda dospeli k záveru, že M =N, t.j. vyhlásenie A(n) platí pre všetky prírodné n.
Metóda dôkazu založená na tejto vete sa nazýva metóda matematickej indukcie, a axióma je axióma indukcie. Tento dôkaz má dve časti:
1) dokázať, že tvrdenie A(n) pravda pre n= A(1);
2) predpokladať, že vyhlásenie A(n) pravda pre n=k, a vychádzajúc z tohto predpokladu dokázať, že tvrdenie A(n) pravda pre n=k+ 1, t.j. že výrok je pravdivý A(k) A(k + 1).
Ak A( 1) A(k) A(k + 1) je pravdivé tvrdenie, potom dospejú k záveru, že tvrdenie A(n) platí pre akékoľvek prirodzené číslo n.
Dôkaz matematickou indukciou môže začať nielen potvrdením pravdivosti tvrdenia za n= 1, ale aj z ľubovoľného prirodzeného čísla m. V tomto prípade vyhlásenie A(n) bude dokázané pre všetky prirodzené čísla nm.
Problém Dokážme, že pre akékoľvek prirodzené číslo platí rovnosť 1 + 3 + 5 ... + (2 n- 1) = n.
Riešenie. Rovnosť 1 + 3 + 5 ... + (2 n- 1) = n je vzorec, ktorý možno použiť na nájdenie súčtu prvých po sebe idúcich nepárnych prirodzených čísel. Napríklad 1 + 3 + 5 + 7 = 4= 16 (súčet obsahuje 4 výrazy), 1 + 3 + 5 + 7 + 9 + 11 = 6= 36 (súčet obsahuje 6 výrazov); ak tento súčet obsahuje 20 výrazov uvedeného typu, potom sa rovná 20 = 400 atď. Po preukázaní pravdivosti tejto rovnosti budeme môcť pomocou vzorca nájsť súčet ľubovoľného počtu členov zadaného typu.
1) Overte pravdivosť tejto rovnosti pre n= 1. Kedy n= 1 ľavú stranu rovnosti tvorí jeden člen rovný 1, pravú stranu rovná 1= 1. Keďže 1 = 1, potom pre n= 1 je táto rovnosť pravdivá.
2) Predpokladajme, že táto rovnosť platí pre n=k, t.j. že 1 + 3 + 5 + … + (2 k- 1) = k. Na základe tohto predpokladu dokážeme, že platí pre n=k+ 1, t.j. 1 + 3 + 5 + ... + (2 k- 1) + (2(k + 1) - 1) = (k + 1).
Zvážte ľavú stranu poslednej rovnosti.
Podľa predpokladu súčet prvého k podmienky je k a preto 1 + 3 + 5 + ... + (2 k- 1) + (2(k + 1) - 1) = 1 + 3 + 5 + … + (2k- 1) + (2k+ 1)=
= k+(2k + 1) = k+ 2k + 1. Výraz k+ 2k + 1 sa identicky rovná výrazu ( k + 1).
Preto pravda o tejto rovnosti pre n=k+ 1 je preukázané.
Táto rovnosť teda platí pre n= 1 a z jeho pravdy za n=k nasleduje pravdu pre n=k+ 1.
To dokazuje, že táto rovnosť platí pre akékoľvek prirodzené číslo.
Pomocou metódy matematickej indukcie možno dokázať pravdivosť nielen rovnosti, ale aj nerovností.
Úloha. Dokáž, že kde nN.
Riešenie. Overme si pravdivosť nerovnosti pre n= 1. Máme - skutočnú nerovnosť.
Predpokladajme, že nerovnosť platí pre n=k, tie. - skutočná nerovnosť. Dokážme na základe predpokladu, že platí pre
n=k+ 1, t.j. 
(*).
Transformujeme ľavú stranu nerovnosti (*), pričom berieme do úvahy, že : .
Ale, to znamená 
.
Takže táto nerovnosť platí pre n= 1, a, zo skutočnosti, že nerovnosť platí pre niektoré n= k, zistili sme, že platí aj pre n= k + 1.
Pomocou axiómy 4 sme teda dokázali, že táto nerovnosť platí pre akékoľvek prirodzené číslo.
Iné tvrdenia možno dokázať aj metódou matematickej indukcie.
Úloha. Dokážte, že tvrdenie platí pre akékoľvek prirodzené číslo.
Riešenie. Overme si pravdivosť tvrdenia n= 1: -pravdivý výrok.
Predpokladajme, že toto tvrdenie platí pre n=k: . Ukážme pomocou toho pravdivosť tvrdenia pre n=k+ 1: 
.
Transformujme výraz: . Poďme nájsť rozdiel k a k+ 1 člen. Ak sa ukáže, že výsledný rozdiel je násobkom 7 a za predpokladu, že subtrahend je deliteľný 7, potom je aj minuend násobkom 7:
Súčin je násobkom 7, teda a .
Toto tvrdenie je teda pravdivé pre n= 1 a z jeho pravdy za n=k nasleduje pravdu pre n=k+ 1.
To dokazuje, že toto tvrdenie platí pre akékoľvek prirodzené číslo.
Úloha. Dokážte to pre akékoľvek prirodzené číslo n 2 tvrdenie (7-1)24 je pravdivé.
Riešenie. 1) Skontrolujte pravdivosť tvrdenia n= 2: - pravdivé tvrdenie.
Metóda matematickej indukcie
Úvod
Hlavná časť
- Úplná a neúplná indukcia
- Princíp matematickej indukcie
- Metóda matematickej indukcie
- Riešenie príkladov
- Rovnosť
- Delenie čísel
- nerovnosti
Záver
Zoznam použitej literatúry
Úvod
Deduktívne a induktívne metódy sú základom každého matematického výskumu. Deduktívnou metódou uvažovania je uvažovanie od všeobecného k jednotlivému, t.j. uvažovanie, ktorého východiskom je všeobecný výsledok a konečným bodom konkrétny výsledok. Indukcia sa uplatňuje pri prechode od konkrétnych výsledkov k všeobecným, t.j. je opakom deduktívnej metódy.
Metódu matematickej indukcie možno porovnať s pokrokom. Začíname od najnižšieho, výsledkom logického myslenia sa dostávame k najvyššiemu. Človek sa vždy snažil o pokrok, o schopnosť logicky rozvíjať svoje myslenie, čo znamená, že samotná príroda mu predurčila myslieť induktívne.
Hoci sa oblasť použitia metódy matematickej indukcie rozrástla, v školských osnovách sa jej venuje málo času. No povedzte, že užitočného človeka privedú tie dve-tri lekcie, na ktoré si vypočuje päť slov teórie, vyrieši päť primitívnych problémov a v dôsledku toho dostane päťku za to, že nič nevie.
Ale toto je také dôležité – vedieť myslieť induktívne.
Hlavná časť
Vo svojom pôvodnom význame sa slovo „indukcia“ používa na uvažovanie, ktorým sa získavajú všeobecné závery založené na množstve konkrétnych tvrdení. Najjednoduchšou metódou uvažovania tohto druhu je úplná indukcia. Tu je príklad takéhoto uvažovania.
Nech je potrebné stanoviť, že každé prirodzené párne číslo n v rámci 4< n < 20 представимо в виде суммы двух простых чисел. Для этого возьмём все такие числа и выпишем соответствующие разложения:
4=2+2; 6=3+3; 8=5+3; 10=7+3; 12=7+5;
14=7+7; 16=11+5; 18=13+5; 20=13+7.
Týchto deväť rovnosti ukazuje, že každé z čísel, ktoré nás zaujímajú, je skutočne reprezentované ako súčet dvoch prvočísel.
Úplnou indukciou teda je, že všeobecné tvrdenie je dokázané oddelene v každom z konečného počtu možných prípadov.
Niekedy možno všeobecný výsledok predpovedať po zvážení nie všetkých, ale skôr veľkého počtu špeciálnych prípadov (takzvaná neúplná indukcia).
Výsledok získaný neúplnou indukciou však zostáva iba hypotézou, kým sa nepreukáže exaktným matematickým uvažovaním, pokrývajúcim všetky špeciálne prípady. Inými slovami, neúplná indukcia v matematike sa nepovažuje za legitímnu metódu rigorózneho dokazovania, ale je mocnou metódou na objavovanie nových právd.
Nech je napríklad potrebné nájsť súčet prvých n po sebe idúcich nepárnych čísel. Zvážte špeciálne prípady:
1+3+5+7+9=25=5 2
Po zvážení týchto niekoľkých špeciálnych prípadov sa navrhuje nasledujúci všeobecný záver:
1+3+5+…+(2n-1)=n 2
tie. súčet prvých n po sebe idúcich nepárnych čísel je n 2
Samozrejme, uskutočnené pozorovanie ešte nemôže slúžiť ako dôkaz platnosti vyššie uvedeného vzorca.
Úplná indukcia má v matematike len obmedzené aplikácie. Mnoho zaujímavých matematických tvrdení pokrýva nekonečný počet špeciálnych prípadov a my nemôžeme testovať nekonečný počet prípadov. Neúplná indukcia často vedie k chybným výsledkom.
V mnohých prípadoch je východiskom z tohto druhu ťažkostí uchýliť sa k špeciálnej metóde uvažovania, nazývanej metóda matematickej indukcie. Je to nasledovné.
Nech je potrebné dokázať platnosť určitého tvrdenia pre ľubovoľné prirodzené číslo n (napr. treba dokázať, že súčet prvých n nepárnych čísel sa rovná n 2). Priame overenie tohto tvrdenia pre každú hodnotu n nie je možné, pretože množina prirodzených čísel je nekonečná. Na dôkaz tohto tvrdenia najskôr skontrolujte jeho platnosť pre n=1. Potom je dokázané, že pre akúkoľvek prirodzenú hodnotu k, platnosť uvažovaného tvrdenia pre n=k implikuje jeho platnosť aj pre n=k+1.
Potom sa tvrdenie považuje za preukázané pre všetky n. Toto tvrdenie skutočne platí pre n=1. Potom však platí aj pre ďalšie číslo n=1+1=2. Platnosť tvrdenia pre n=2 implikuje jeho platnosť pre n=2+
1=3. To znamená platnosť tvrdenia pre n=4 atď. Je jasné, že nakoniec sa dostaneme k akémukoľvek prirodzenému číslu n. Preto tvrdenie platí pre každé n.
Zhrnutím toho, čo bolo povedané, sformulujeme nasledujúci všeobecný princíp.
Princíp matematickej indukcie.
Ak veta A(n), ktorá závisí od prirodzeného čísla n, platí pre n=1 a z toho, že platí pre n=k (kde k je ľubovoľné prirodzené číslo), vyplýva, že je aj platí pre nasledujúce číslo n=k +1, potom Predpoklad A(n) platí pre každé prirodzené číslo n.
V mnohých prípadoch môže byť potrebné dokázať platnosť určitého tvrdenia nie pre všetky prirodzené čísla, ale iba pre n>p, kde p je pevné prirodzené číslo. V tomto prípade je princíp matematickej indukcie formulovaný nasledovne.
Ak výrok A(n) platí pre n=p a ak A(k)ÞA(k+1) pre ľubovoľné k>p, potom výrok A(n) platí pre ľubovoľné n>p.
Dôkaz metódou matematickej indukcie sa vykonáva nasledovne. Najprv sa skontroluje tvrdenie, ktoré sa má dokázať, na n=1, t.j. je potvrdená pravdivosť výroku A(1). Táto časť dôkazu sa nazýva indukčná báza. Potom nasleduje časť dôkazu nazývaná indukčný krok. V tejto časti je dokázaná platnosť tvrdenia pre n=k+1 za predpokladu, že tvrdenie platí pre n=k (induktívny predpoklad), t.j. dokázať, že A(k)ÞA(k+1).
Dokážte, že 1+3+5+…+(2n-1)=n 2 .
Riešenie: 1) Máme n=1=1 2 . teda
tvrdenie je pravdivé pre n=1, t.j. A(1) je pravda.
2) Dokážme, že A(k)ÞA(k+1).
Nech k je ľubovoľné prirodzené číslo a výrok nech platí pre n=k, t.j.
1+3+5+…+(2k-1)=k2.
Dokážme, že potom tvrdenie platí aj pre ďalšie prirodzené číslo n=k+1, t.j. čo
1+3+5+…+(2k+1)=(k+1)2.
Naozaj,
1+3+5+…+(2k-1)+(2k+1)=k2+2k+1=(k+1)2.
Takže A(k)ÞA(k+1). Na základe princípu matematickej indukcie sme dospeli k záveru, že predpoklad A(n) platí pre akékoľvek nОN.
Dokáž to
1+x+x 2 +x 3 +…+x n =(x n+1 -1)/(x-1), kde x¹1
Riešenie: 1) Pre n=1 dostaneme
1+x=(x2-1)/(x-1)=(x-1)(x+1)/(x-1)=x+1
preto pre n=1 platí vzorec; A(1) je pravda.
2) Nech k je ľubovoľné prirodzené číslo a vzorec nech platí pre n=k, t.j.
1 + x + x 2 + x 3 + ... + x k \u003d (x k + 1 -1) / (x-1).
Dokážme, že potom tá rovnosť
1+x+x 2 +x 3 +…+x k +x k+1 =(x k+2 -1)/(x-1).
Naozaj
1+х+х 2 +x 3 +…+х k +x k+1 =(1+x+x 2 +x 3 +…+x k)+x k+1 =
=(xk+1-1)/(x-1)+xk+1 =(xk+2-1)/(x-1).
Takže A(k)ÞA(k+1). Na základe princípu matematickej indukcie sme dospeli k záveru, že vzorec platí pre akékoľvek prirodzené číslo n.
Dokážte, že počet uhlopriečok konvexného n-uholníka je n(n-3)/2.
Riešenie: 1) Pre n=3 je tvrdenie pravdivé
A 3 je správne, pretože v trojuholníku
A 3 =3(3-3)/2=0 uhlopriečok;
A 2 A(3) je pravdivé.
2) Predpokladajme, že v akomkoľvek
konvexný k-uholník má-
A 1 sya A k \u003d k (k-3) / 2 uhlopriečky.
A k Dokážme, že potom v konvexnom
(k+1)-gon číslo
uhlopriečky A k+1 =(k+1)(k-2)/2.
Nech А 1 А 2 А 3 …A k A k+1 -konvexný (k+1)-uhol. Narysujme do nej uhlopriečku A 1 A k. Na spočítanie celkového počtu uhlopriečok tohto (k + 1)-uholníka je potrebné spočítať počet uhlopriečok v k-uholníku A 1 A 2 ...A k , k výslednému číslu pripočítať k-2, t.j. treba brať do úvahy počet uhlopriečok (k+1)-uholníka vychádzajúceho z vrcholu A k+1 a navyše uhlopriečku A 1 A k.
Touto cestou,
k+1 = k +(k-2)+1=k(k-3)/2+k-1=(k+1)(k-2)/2.
Takže A(k)ÞA(k+1). Vzhľadom na princíp matematickej indukcie je tvrdenie pravdivé pre akýkoľvek konvexný n-uholník.
Dokážte, že pre akékoľvek n je tvrdenie pravdivé:
1 2 +2 2 +3 2 +…+n 2 =n(n+1)(2n+1)/6.
Riešenie: 1) Nech n=1
X 1 \u003d 1 2 \u003d 1 (1 + 1) (2 + 1) / 6 \u003d 1.
Pre n=1 je teda tvrdenie pravdivé.
2) Predpokladajme, že n=k
X k \u003d k 2 \u003d k (k + 1) (2k + 1) / 6.
3) Uvažujme toto tvrdenie pre n=k+1
Xk+1 = (k+1)(k+2)(2k+3)/6.
X k+1 =1 2 +2 2 +3 2 +…+k 2 +(k+1) 2 =k(k+1)(2k+1)/6+ +(k+1) 2 =(k (k+1)(2k+1)+6(k+1) 2)/6=(k+1)(k(2k+1)+
6(k+1))/6=(k+1)(2k 2 +7k+6)/6=(k+1)(2(k+3/2)(k+
2))/6=(k+1)(k+2)(2k+3)/6.
Dokázali sme platnosť rovnosti pre n=k+1, preto na základe metódy matematickej indukcie platí tvrdenie pre každé prirodzené n.
Dokážte, že pre akékoľvek prirodzené n platí rovnosť:
1 3 +2 3 +3 3 +…+n 3 =n 2 (n+1) 2 /4.
Riešenie: 1) Nech n=1.
Potom X 1 = 1 3 = 1 2 (1+1) 2 /4 = 1.
Vidíme, že pre n=1 je tvrdenie pravdivé.
2) Predpokladajme, že rovnosť platí pre n=k
X k \u003d k 2 (k + 1) 2/4.
3) Dokážme pravdivosť tohto tvrdenia pre n=k+1, t.j.
Xk+1 = (k+1)2(k+2)2/4. X k+1 = 1 3 +2 3 +…+k 3 +(k+1) 3 =k 2 (k+1) 2 /4+(k+1) 3 = (k 2 (k++1) 2+4(k+1)3)/4=(k+1)2(k2+4k+4)/4=(k+1)2(k+2)2/4.
Z vyššie uvedeného dôkazu je zrejmé, že tvrdenie platí pre n=k+1, teda rovnosť platí pre akékoľvek prirodzené n.
Dokáž to
((2 3 +1)/(2 3 -1))´((3 3 +1)/(3 3 -1))´…´((n 3 +1)/(n 3 -1))= 3n(n+1)/2(n2+n+1), kde n>2.
Riešenie: 1) Pre n=2 identita vyzerá takto: (2 3 +1)/(2 3 -1)=(3´2´3)/2(2 2 +2+1),
tie. je to správne.
2) Predpokladajme, že výraz platí pre n=k
(2 3 +1)/(2 3 -1)´...´(k 3 +1)/(k 3 -1)=3k(k+1)/2(k2+k+1).
3) Dokážeme správnosť výrazu pre n=k+1.
(((2 3 +1)/(2 3 -1))´…´((k 3 +1)/(k 3 -1)))´(((k+1) 3 +
1)/((k+1) 3 -1))=(3k(k+1)/2(k 2 +k+1))'((k+2)((k+
1) 2 -(k+1)+1)/k((k+1) 2 +(k+1)+1))=3(k+1)(k+2)/2´
´((k+1)2 +(k+1)+1).
Dokázali sme platnosť rovnosti pre n=k+1, preto vzhľadom na metódu matematickej indukcie platí tvrdenie pre ľubovoľné n>2
Dokáž to
1 3 -2 3 +3 3 -4 3 +…+(2n-1) 3 -(2n) 3 =-n 2 (4n+3)
pre akékoľvek prirodzené n.
Riešenie: 1) Nech n=1
1 3 -2 3 =-1 3 (4+3); -7=-7.
2) Predpokladajme, že n=k
1 3 -2 3 +3 3 -4 3 +…+(2k-1) 3-(2k)3 =-k2 (4k+3).
3) Dokážme pravdivosť tohto tvrdenia pre n=k+1
(1 3 -2 3 +…+(2k-1) 3 -(2k) 3)+(2k+1) 3 -(2k+2) 3 =-k 2 (4k+3)+
+(2k+1)3-(2k+2)3 =-(k+1)3 (4(k+1)+3).
Dokázaná je aj platnosť rovnosti pre n=k+1, preto tvrdenie platí pre ľubovoľné prirodzené číslo n.
Dokážte platnosť totožnosti
(1 2 /1´3)+(2 2 /3´5)+…+(n 2 /(2n-1)´(2n+1))=n(n+1)/2(2n+1)
pre akékoľvek prirodzené n.
1) Pre n=1 je identita pravdivá 1 2 /1´3=1(1+1)/2(2+1).
2) Predpokladajme, že pre n=k
(1 2 /1´3)+…+(k2/(2k-1)´(2k+1))=k(k+1)/2(2k+1).
3) Dokážme, že totožnosť platí pre n=k+1.
(1 2 /1´3)+…+(k 2 /(2k-1)(2k+1))+(k+1) 2 /(2k+1)(2k+3)=(k(k+ 1) )/2(2k+1))+((k+1) 2 /(2k+1)(2k+3))=((k+1)/(2k+1))´((k/2) +((k+1)/(2k+3)))=(k+1)(k+2)´ (2k+1)/2(2k+1)(2k+3)=(k+1) (k+2)/2(2(k+1)+1).
Z vyššie uvedeného dôkazu je zrejmé, že tvrdenie platí pre každé prirodzené číslo n.
Dokážte, že (11 n+2 +12 2n+1) je bezo zvyšku deliteľné číslom 133.
Riešenie: 1) Nech n=1
11 3 + 12 3 \u003d (11 + 12) (11 2 -132 + 12 2) \u003d 23´133.
Ale (23´133) je deliteľné 133 bezo zvyšku, takže pre n=1 je tvrdenie pravdivé; A(1) je pravda.
2) Predpokladajme, že (11 k+2 +12 2k+1) je deliteľné číslom 133 bezo zvyšku.
3) Dokážme to v tomto prípade
(11 k+3 +12 2k+3) je deliteľné 133 bezo zvyšku. Skutočne, 11 k+3 +12 2k+3 = 11´11 k+2 +12 2´ 12 2k+1 = 11´11 k+2 +
+(11+133)´12 2k+1 =11(11 k+2 +12 2k+1)+133´12 2k+1 .
Výsledný súčet je bezo zvyšku deliteľný číslom 133, pretože jeho prvý člen je bezo zvyšku deliteľný číslom 133 a druhý člen je deliteľný číslom 133. Takže А(k)ÞА(k+1). Pomocou metódy matematickej indukcie je tvrdenie dokázané.
Dokážte, že pre ľubovoľné n je n -1 deliteľné číslom 6 bezo zvyšku.
Riešenie: 1) Nech n=1, potom X 1 =7 1 -1=6 delíme 6 bezo zvyšku. Takže pre n=1 je tvrdenie pravdivé.
2) Predpokladajme, že pre n=k
7 k -1 je deliteľné 6 bezo zvyšku.
3) Dokážme, že tvrdenie platí pre n=k+1.
Xk+1=7k+1-1=7'7 k-7+6=7(7k-1)+6.
Prvý člen je deliteľný 6, pretože 7 k -1 je deliteľných 6 za predpokladu, a druhý člen je 6. Takže 7 n -1 je násobkom 6 pre akékoľvek prirodzené n. Pomocou metódy matematickej indukcie je tvrdenie dokázané.
Dokážte, že 3 3n-1 +2 4n-3 pre ľubovoľné prirodzené n je deliteľné 11.
Riešenie: 1) Nech n=1
X 1 \u003d 3 3-1 +2 4-3 \u003d 3 2 +2 1 \u003d 11 sa vydelí 11 bez zvyšku. Pre n=1 je teda tvrdenie pravdivé.
2) Predpokladajme, že pre n=k
X k \u003d 3 3k-1 +2 4k-3 je bezo zvyšku deliteľné 11.
3) Dokážme, že tvrdenie platí pre n=k+1.
X k+1 =3 3(k+1)-1 +2 4(k+1)-3 =3 3k+2 +2 4k+1 =3 3' 3 3k-1 +2 4' 2 4k-3 =
27´3 3k-1 +16´2 4k-3 =(16+11)´3 3k-1 +16´2 4k-3 =16´3 3k-1 +
11´3 3k-1 +16´2 4k-3 =16(3 3k-1 +2 4k-3)+11´3 3k-1 .
Prvý člen je deliteľný 11 bezo zvyšku, keďže 3 3k-1 +2 4k-3 je deliteľné 11 za predpokladu, druhý člen je deliteľný 11, pretože jedným z jeho faktorov je číslo 11. Súčet je teda deliteľné aj 11 bezo zvyšku pre ľubovoľné prirodzené n. Pomocou metódy matematickej indukcie je tvrdenie dokázané.
Dokážte, že 11 2n -1 pre ľubovoľné kladné celé číslo n je bezo zvyšku deliteľné 6.
Riešenie: 1) Nech n=1, potom 11 2 -1=120 je deliteľné 6 bezo zvyšku. Takže pre n=1 je tvrdenie pravdivé.
2) Predpokladajme, že pre n=k
11 2k -1 je deliteľné 6 bezo zvyšku.
11 2(k+1) -1=121´11 2k -1=120´11 2k +(11 2k -1).
Oba členy sú bezo zvyšku deliteľné 6: prvý obsahuje násobok 6 číslo 120 a druhý je deliteľný 6 bezo zvyšku podľa predpokladu. Čiže súčet je bezo zvyšku deliteľný 6. Pomocou metódy matematickej indukcie je tvrdenie dokázané.
Dokážte, že 3 3n+3 -26n-27 pre ľubovoľné kladné celé číslo n je bezo zvyšku deliteľné číslom 26 2 (676).
Riešenie: Najprv dokážme, že 3 3n+3 -1 je bezo zvyšku deliteľné 26.
- Pre n=0
- Predpokladajme, že pre n=k
- Dokážme, že tvrdenie
3 3 -1 = 26 je deliteľné 26
3 3k+3 -1 je deliteľné 26
platí pre n=k+1.
3 3k+6 -1=27´3 3k+3 -1=26´3 3k+3 +(3 3k+3 -1) – deliteľné 26
Teraz dokážme tvrdenie formulované v podmienke problému.
1) Je zrejmé, že pre n=1 je tvrdenie pravdivé
3 3+3 -26-27=676
2) Predpokladajme, že pre n=k
výraz 3 3k+3 -26k-27 je deliteľný 26 2 bezo zvyšku.
3) Dokážme, že tvrdenie platí pre n=k+1
333k+6-26(k+1)-27=26(333k+3-1)+(33k+3-26k-27).
Oba členy sú deliteľné 26 2 ; prvý je deliteľný 26 2, pretože sme dokázali, že výraz v zátvorke je deliteľný 26, a druhý je deliteľný induktívnou hypotézou. Pomocou metódy matematickej indukcie je tvrdenie dokázané.
Dokážte, že ak n>2 a x>0, potom nerovnosť
(1+x) n >1+n´x.
Riešenie: 1) Pre n=2 je nerovnosť pravdivá, pretože
(1+x)2 = 1+2x+x2 >1+2x.
Takže A(2) je pravda.
2) Dokážme, že A(k)ÞA(k+1), ak k> 2. Predpokladajme, že A(k) platí, t.j. že nerovnosť
(1+x) k >1+k´x. (3)
Dokážme, že potom platí aj A(k+1), t.j. že nerovnosť
(1+x) k+1 >1+(k+1)'x.
Vynásobením oboch strán nerovnosti (3) kladným číslom 1+x dostaneme
(1+x) k+1 >(1+k´x)(1+x).
Zvážte pravú stranu posledného nerovného
stva; máme
(1+k´x)(1+x)=1+(k+1)´x+k´x 2 >1+(k+1)´x.
Výsledkom je, že to dostaneme
(1+x) k+1 >1+(k+1)'x.
Takže A(k)ÞA(k+1). Na základe princípu matematickej indukcie možno tvrdiť, že Bernoulliho nerovnosť platí pre všetky
Dokážte, že nerovnosť je pravdivá
(1+a+a2) m > 1+m´a+(m(m+1)/2)´a2 pre a> 0.
Riešenie: 1) Pre m=1
(1+a+a 2) 1 > 1+a+(2/2)´a 2 obe časti sú rovnaké.
2) Predpokladajme, že pre m=k
(1+a+a 2) k >1+k´a+(k(k+1)/2)´a 2
3) Dokážme, že pre m=k+1 je nerovnosť pravdivá
(1+a+a 2) k+1 =(1+a+a 2)(1+a+a 2) k >(1+a+a 2)(1+k´a+
+(k(k+1)/2)´a 2)=1+(k+1)´a+((k(k+1)/2)+k+1)´a 2 +
+((k(k+1)/2)+k)´a 3 +(k(k+1)/2)´a 4 > 1+(k+1)´a+
+((k+1)(k+2)/2)'a2.
Dokázali sme platnosť nerovnosti pre m=k+1, preto pomocou metódy matematickej indukcie platí nerovnosť pre akékoľvek prirodzené m.
Dokážte, že pre n>6 je nerovnosť
3 n > n'2 n+1.
Riešenie: Prepíšme nerovnosť do tvaru
- Pre n=7 máme
- Predpokladajme, že pre n=k
3 7 /2 7 =2187/128>14=2´7
nerovnosť je pravdivá.
3) Dokážme správnosť nerovnosti pre n=k+1.
3k+1 /2k+1 =(3k/2k)´(3/2)>2k´(3/2)=3k>2(k+1).
Od k>7 je zrejmá posledná nerovnosť.
Na základe metódy matematickej indukcie platí nerovnosť pre akékoľvek prirodzené n.
Dokážte, že pre n>2 je nerovnosť
1+(1/2 2)+(1/3 2)+…+(1/n 2)<1,7-(1/n).
Riešenie: 1) Pre n=3 platí nerovnosť
1+(1/2 2)+(1/3 2)=245/180<246/180=1,7-(1/3).
- Predpokladajme, že pre n=k
1+(1/2 2)+(1/3 2)+…+(1/k 2)=1,7-(1/k).
3) Preukážeme platnosť ne-
rovnosti pre n=k+1
(1+(1/2 2)+…+(1/k 2))+(1/(k+1) 2)<1,7-(1/k)+(1/(k+1) 2).
Dokážme, že 1,7-(1/k)+(1/(k+1) 2)<1,7-(1/k+1)Û
w(1/(k+1) 2)+(1/k+1)<1/kÛ(k+2)/(k+1) 2 <1/kÛ
Ûk(k+2)<(k+1) 2Û k 2 +2k To druhé je zrejmé, a preto 1+(1/2 2)+(1/3 2)+…+(1/(k+1) 2)<1,7-(1/k+1). Pomocou metódy matematickej indukcie je nerovnosť dokázaná. Záver Najmä po preštudovaní metódy matematickej indukcie som zlepšil svoje znalosti v tejto oblasti matematiky a tiež som sa naučil, ako riešiť problémy, ktoré boli predtým mimo moju silu. V podstate to boli logické a zábavné úlohy, t.j. práve tie, ktoré zvyšujú záujem o samotnú matematiku ako vedu. Riešenie takýchto úloh sa stáva zábavnou činnosťou a dokáže prilákať do matematických labyrintov stále viac zvedavcov. To je podľa mňa základ každej vedy. Pokračovaním v štúdiu metódy matematickej indukcie sa pokúsim naučiť ju aplikovať nielen v matematike, ale aj pri riešení úloh vo fyzike, chémii a živote samotnom. MATEMATIKA: PREDNÁŠKY, ÚLOHY, RIEŠENIA Učebnica / V. G. Boltyansky, Yu. V. Sidorov, M. I. Shabunin. Potpourri LLC 1996. ALGEBRA A PRINCÍPY ANALÝZY Učebnica / I. T. Demidov, A. N. Kolmogorov, S. I. Shvartsburg, O. S. Ivashev-Musatov, B. E. Veits. "Osvietenie" 1975. MBOU lýceum "Technické a ekonomické"
METÓDA MATEMATICKEJ INDUKCIE
METÓDA MATEMATICKEJ INDUKCIE.
VYSVETLIVKA
Pre žiakov 10. ročníka matematického profilu bol zostavený metodický vývoj „Metóda matematickej indukcie“. Primárne ciele: oboznámiť študentov s metódou matematickej indukcie a naučiť ju aplikovať pri riešení rôznych problémov. V metodickom vývoji sa zvažujú otázky elementárnej matematiky: problémy deliteľnosti, preukazovanie totožnosti, preukazovanie nerovností, sú navrhnuté problémy rôzneho stupňa zložitosti, vrátane problémov ponúkaných na olympiádach. Úloha induktívnych inferencií v experimentálnych vedách je veľmi veľká. Dávajú tie ustanovenia, z ktorých sa potom odvodzujú ďalšie závery. názov metóda matematickej indukcie klamlivo – v skutočnosti je táto metóda deduktívna a poskytuje presný dôkaz tvrdení uhádnutých indukciou. Metóda matematickej indukcie prispieva k identifikácii súvislostí medzi rôznymi úsekmi matematiky, pomáha rozvíjať matematickú kultúru žiaka. Definícia metódy matematickej indukcie. Úplná a neúplná indukcia. Dôkaz nerovností. Dôkaz totožnosti. Riešenie problémov s deliteľnosťou. Riešenie rôznych úloh na tému "Metóda matematickej indukcie". LITERATÚRA PRE UČITEĽA
1. M. L. Galitsky. Hĺbkové štúdium priebehu algebry a matematickej analýzy. - M. Osvietenstvo. 1986. 2. L. I. Zvavich. Algebra a začiatky analýzy. Didaktické materiály. M. Drofa, 2001. 3. N.Ya.Vilenkin. Algebra a matematická analýza. M Osvietenie. 1995. 4. Yu.V. Micheev. Metóda matematickej indukcie. NGU.1995. LITERATÚRA PRE ŠTUDENTOV
1. N.Ya. Vilenkin. Algebra a matematická analýza. M Osvietenie. 1995. 2. Yu.V. Micheev. Metóda matematickej indukcie. NGU.1995. KĽÚČOVÉ SLOVÁ
Indukcia, axióma, princíp matematickej indukcie, úplná indukcia, neúplná indukcia, tvrdenie, identita, nerovnosť, deliteľnosť. DIDAKTICKÁ PRÍLOHA K TÉME
„METÓDA MATEMATICKEJ INDUKCIE“.
Lekcia 1
Definícia metódy matematickej indukcie.
Metóda matematickej indukcie je jednou z vysoko efektívnych metód na hľadanie nových výsledkov a dokazovanie pravdivosti uvedených predpokladov. Hoci táto metóda nie je v matematike nová, záujem o ňu neutícha. Prvýkrát v prehľadnom podaní metódu matematickej indukcie aplikoval v 17. storočí vynikajúci francúzsky vedec Blaise Pascal pri dokazovaní vlastností číselného trojuholníka, ktorý je odvtedy po ňom pomenovaný. Myšlienka matematickej indukcie však bola známa už starým Grékom. Metóda matematickej indukcie je založená na princípe matematickej indukcie, ktorá je akceptovaná ako axióma. Budeme uvažovať o myšlienke matematickej indukcie s príkladmi. Príklad č. 1.
Štvorec je rozdelený segmentom na dve časti, potom je jedna z výsledných častí rozdelená na dve časti atď. Určte, na koľko častí je štvorec rozdelený P kroky? Riešenie. Po prvom kroku dostaneme podľa podmienok 2 diely. V druhom kroku necháme jednu časť nezmenenú a druhú rozdelíme na 2 časti a získame 3 časti. V treťom kroku necháme 2 časti nezmenené a tretiu rozdelíme na dve časti a získame 4 časti. Vo štvrtom kroku necháme 3 časti nezmenené a poslednú časť rozdelíme na dve časti a získame 5 častí. V piatom kroku dostaneme 6 dielov. Návrh sa robí cez P kroky, ktoré dostaneme (n+1)časť. Tento návrh však treba dokázať. Predpokladajme, že cez Komu kroky, na ktoré je námestie rozdelené (k+1)časť. Potom ďalej (k+1) krok my Komučasti zostanú nezmenené a (k+1) rozdeľte časť na dve časti a získajte (k+2)časti. Všimli ste si, že takto sa môžete hádať, ako dlho chcete, do nekonečna. To znamená, že náš predpoklad je taký P kroky štvorec bude rozdelený na (n+1)časť, sa stáva preukázanou. Príklad č. 2.
Moja stará mama mala vnučku, ktorá mala veľmi rada džem, a najmä ten v litrovom tégliku. Babička mu ale dotyk nedovolila. A vnučky sa rozhodli svoju babičku oklamať. Rozhodol sa zjesť každý deň 1/10 litra z tejto nádoby a doliať ju vodou a dôkladne premiešať. Po koľkých dňoch babička odhalí podvod, ak džem zostane rovnaký, keď sa zriedi vodou na polovicu? Riešenie. Zistite, koľko čistého džemu potom zostane v pohári P dni. Po prvom dni zostane zmes v tégliku zložená z 9/10 džemu a 1/10 vody. Po dvoch dňoch 1/10 zmesi vody a džemu z pohára zmizne a zostane (1 liter zmesi obsahuje 9/10 l džemu, 1/10 l zmesi obsahuje 9/100 l džemu) 9/10 - 9/100=81/100=(9/10) 2 litre džemu. Na tretí deň z pohára zmizne 1/10 litra zmesi pozostávajúcej z džemu 81/100 a 19/100 vody. V 1 litri zmesi je 81/100 litrov džemu, v 1/10 litra zmesi 81/1000 litrov džemu. 81/100 – 81/1000= 729/1000=(9/10) Po 3 dňoch zostanú 3 litre džemu a zvyšok zaberie voda. Objaví sa vzor. Naprieč P zostávajúce dni v banke (9/10) P l džem. Ale opäť je to len náš odhad. Nechaj Komu je ľubovoľné prirodzené číslo. Predpokladajme, že cez Komu dní v banke zostane (9/10) do l džem. Uvidíme, čo bude v banke o ďalší deň, teda v (k+1) deň. Zmiznú z banky 1/10 l zmes (9/10)
Komu l džem a voda. V 1 l zmes je (9/10)
Komu l džem, v 1/10 l zmesi (9/10)
k+1 l džem. Teraz to môžeme bezpečne povedať P zostávajúce dni v banke (9/10)
P l džem. Do 6 dní bude mať banka 531444/1000000l džemy, po 7 dňoch - 4782969/10000000l džem, teda menej ako polovicu. odpoveď: po 7 dnoch babatko podvod odhali. Pokúsme sa vybrať najzákladnejšie v riešeniach uvažovaných problémov. Každý z nich sme začali riešiť zvažovaním samostatných alebo, ako sa hovorí, špeciálnych prípadov. Potom sme na základe našich pozorovaní urobili nejaké predpoklady P(n), v závislosti od prirodzeného P.
tvrdenie bolo skontrolované, teda preukázané P(1), P(2), P(3);
navrhol to P(n) platný na n=k a vydedukoval, že potom to bude platiť aj na ďalšie n, n=k+1.
A potom sa hádali asi takto: P(1) správny, P(2) správny, P(3) správny, P(4) správne... je to tak P(n).
Princíp matematickej indukcie.
Vyhlásenie P(n), v závislosti od prirodzeného P, platí pre všetky prírodné P, ak 1) platnosť tvrdenia pre n = 1;
2) z predpokladu platnosti výpisu P(n) pri n=k by mal Spravodlivosť P(n) pri n=k+1.
V matematike sa princíp matematickej indukcie spravidla volí ako jedna z axióm, ktoré definujú prirodzený rad čísel, a preto sa prijíma bez dôkazu. Metóda dôkazu princípom matematickej indukcie sa zvyčajne nazýva metóda matematickej indukcie. Všimnite si, že táto metóda je široko používaná pri dokazovaní teorémov, identít, nerovností pri riešení problémov deliteľnosti a mnohých ďalších problémov. Lekcia č. 2
Úplná a neúplná indukcia.
V prípade, že sa matematický výrok týka konečného počtu objektov, možno ho dokázať kontrolou každého objektu, napríklad výrokom „Každé dvojciferné párne číslo je súčtom dvoch prvočísel“. Metóda dôkazu, pri ktorej testujeme tvrdenie pre konečný počet prípadov, sa nazýva úplná matematická indukcia. Táto metóda sa používa pomerne zriedkavo, pretože výroky sa najčastejšie zvažujú na nekonečných množinách. Napríklad veta „Akékoľvek párne číslo sa rovná súčtu dvoch prvočísel“ nebola doteraz ani dokázaná, ani vyvrátená. Aj keby sme túto vetu otestovali pre prvú miliardu, nepriblížilo by nás to ani o krok bližšie k jej preukázaniu. V prírodných vedách sa používa neúplná indukcia, testovanie experimentu niekoľkokrát, prenášanie výsledku do všetkých prípadov. Príklad č. 3
Uhádnite pomocou neúplného indukčného vzorca pre súčet kociek prirodzených čísel. Riešenie. 1 3 =1; 1 3 +2 3 =(1+2) 2 ; 1 3 +2 3 +3 3 =(1+2+3) 2 ; 1 3 +2 3 +3 3 +4 3 =(1+2+3+4) 2 ;
1 3 +2 3 +3 3 +4 3 +5 3 =(1+2+3+4+5) 2 ; …; 1 3 +2 3 +…+n 3 =(1+2+…+n) 2 . Dôkaz. Nech je to pravda pre n=k.
Dokážme, že to platí pre n=k+1.
Záver: vzorec pre súčet kociek prirodzených čísel platí pre každé prirodzené P.
Príklad č. 4
Uvažujte o rovnosti a hádajte, k akému všeobecnému zákonu tieto príklady vedú. Riešenie. 1=0+1
2+3+4=1+8
5+6+7+8+9=8+27
10+11+12+13+14+15+16=27+64
17+18+19+20+21+22+23+24+25=64+125
……………………………………………………………..
Príklad č. 5
Napíšte nasledujúce výrazy ako súčet: 1) Príklad č. 6.
Zapíšte nasledujúce sumy pomocou znamienka 2) Príklad č. 7.
Napíšte nasledujúce výrazy ako produkty: 1) 3) Príklad č. 8.
Zapíšte si nasledujúce diela pomocou znamienka (veľké grécke písmeno "pi") 1) Príklad #9.
Výpočet hodnoty polynómu Je tento predpoklad správny? Riešenie. Ak je každý sčítanec deliteľný číslom, potom je súčet deliteľný týmto číslom, Analýza konečného počtu prípadov hrá v matematike dôležitú úlohu: bez toho, aby sme poskytli dôkaz o jednom alebo druhom tvrdení, pomáha uhádnuť správnu formuláciu tohto tvrdenia, ak ešte nie je známe. Takto prišiel Goldbach, člen Petrohradskej akadémie vied, k domnienke, že každé prirodzené číslo, počnúc dvojkou, je súčtom najviac troch prvočísel. Lekcia č. 3
Metóda matematickej indukcie nám umožňuje dokázať rôzne identity. Príklad #10. Dokážme to všetkým P identitu Riešenie. Položme Musíme to dokázať Dokážme, že Potom z pravdy identity Podľa princípu matematickej indukcie, pravda identity pre všetkých P.
Príklad č. 11.
Dokážme totožnosť Dôkaz. medziročné rovnosti. Lekcia číslo 4.
Dôkaz identity matematickou indukciou.
Príklad č. 12.
Dokážme totožnosť Dôkaz. Aplikovaním princípu matematickej indukcie sme dokázali, že rovnosť platí pre všetkých P.
Príklad č. 13.
Dokážme totožnosť Dôkaz. Aplikovaním princípu matematickej indukcie sme dokázali, že toto tvrdenie platí pre akékoľvek prírodné P.
Príklad č. 14.
Dokážme totožnosť Dôkaz. Príklad č. 15.
Dokážme totožnosť 1)
n = 1;
2) pre n=k
rovnosť 3) dokázať, že platí rovnosť n=k+1:
Záver: identita je platná pre každú prirodzenú P.
Príklad č. 16. Dokážme totožnosť Dôkaz. Ak n=1
, potom Nech platí identita n=k.
Dokážme, že totožnosť platí n=k+1.
Potom je identita platná pre akékoľvek prirodzené P.
Lekcia číslo 5.
Dôkaz identity matematickou indukciou.
Príklad č. 17. Dokážme totožnosť Dôkaz. Ak n=2
, potom dostaneme správnu rovnosť: Nech platí rovnosť pren=k:
Dokážme platnosť tvrdenia pre n=k+1.
Podľa princípu matematickej indukcie sa identita dokazuje. Príklad č. 18.
Dokážme totožnosť o n=2
táto identita sa dá prepísať veľmi jednoduchou formou a zjavne pravdivé. Nechajte pri n=k naozaj Dokážme platnosť tvrdenia pren=k+1,
to znamená, že je splnená rovnosť: . Takže sme dokázali, že identita je pravdivá pre akékoľvek prírodné n≥2.
Príklad č. 19.
Dokážme totožnosť o n=1
dostaneme správnu rovnosť: Predpokladajme, že pri n=k získame tiež správnu rovnosť: Dokážme, že platnosť rovnosti je dodržaná pre n=k+1:
Potom je identita platná pre akékoľvek prirodzené P.
Lekcia číslo 6.
Riešenie problémov s deliteľnosťou.
Príklad #20. Dokážte to matematickou indukciou Dôkaz. o n=1
existuje rozdelenie na6
bez stopy, Nechajte pri n=k
výraz Dokážme, že kedy n=k+1
výraz Každý výraz je násobkom 6
, takže súčet je násobkom 6
.
Príklad číslo 21.
Dôkaz. o n=1
výraz je deliteľný Nechajte pri n=k
výraz o n=k+1 deleno 5
.
Príklad č. 22.
Dokážte deliteľnosť výrazu Dôkaz. o n=1 viacnásobný 16
.
Nechajte pri n=k
o n=k+1
Všetky pojmy sú deliteľné 16:
prvý je zjavne druhý podľa predpokladu a tretí má v zátvorkách párne číslo. Príklad #23.
Dokážte deliteľnosť Dôkaz. Najprv to dokážme o n=0
Nechajte pri n=k
Potom o n=k+1 deleno 26
.
Dokážme teraz tvrdenie formulované v podmienke problému. o n=1 deleno 676.
o n=k
to je pravda o n=k+1
.
Oba pojmy sú deliteľné 676
; prvá je preto, že sme dokázali deliteľnosť tým 26
výraz v zátvorkách a druhý je deliteľný induktívnou hypotézou. Lekcia číslo 7.
Riešenie problémov s deliteľnosťou.
Príklad číslo 24.
Dokáž to Dôkaz. o n=1
o n=k
o n=k+1
každý výraz je deliteľný5
bez stopy. Príklad č. 25.
Dokáž to Dôkaz. o n=1
Nechajte pri n=k
o n=k+1 deleno 6
žiadny zvyšok, pretože každý člen je deliteľný6
bezo zvyšku: prvý člen podľa induktívneho predpokladu, druhý, samozrejme, tretí, pretože Príklad č. 26.
Dokáž to Dôkaz. Dokážme to o n=1 o n=k+1 deleno 9
.
Príklad číslo 27.
Dokážte, že je deliteľné15
bez stopy. Dôkaz. o n=1 deleno 15
.
Nechajte pri n=k deleno 15
bez stopy. o n=k+1
Prvý člen je násobok15
podľa indukčnej hypotézy je druhý člen násobkom15
– samozrejme, že tretí člen je násobkom15
, pretože Lekcia číslo 8-9.
Dôkaz nerovností matematickou indukciou
Príklad #28. o n=1 máme Nechajte pri n=k o n=k+1 Potom nerovnosť platí pre akékoľvek prírodné P. Príklad #29. Dokážte, že nerovnosť je pravdivá o n=1 dostaneme správnu nerovnosť 4 >1.
Nechajte pri n=k nerovnosť Dokážme, že kedy n=k+1 nerovnosť Pre akékoľvek prírodné Komu pozoruje sa nerovnosť. Ak Príklad #30. Nechaj n=1 Predpokladajme, že nerovnosť platí n=k: o n=k+1 Príklad číslo 31. Dokážte platnosť nerovnosti Najprv dokážme, že pre akékoľvek prírodné T nerovnosť o n=1 pôvodná nerovnosť je pravdivá Nech platí nerovnosť n=k: o n=k+1 Lekcia číslo 10.
Riešenie problémov k téme
Metóda matematickej indukcie.
Príklad #32. Dokážte Bernoulliho nerovnosť. Ak Dôkaz. o n=1
dokazovaná nerovnosť má formu Keďže podľa stavu Pretože Takže nerovnosť platí pre n=1, a z jeho pravdy na n=k z toho vyplýva, že je pravdivé a n=k+1. Matematickou indukciou to teda platí pre všetkých prirodzených P.
napr. Príklad číslo 33.
Nájdite všetky prírodné hodnotyP
, pre ktoré je nerovnosť Riešenie. o n=1 nerovnosť je správna. o n=2 nerovnosť je tiež pravda. o n=3 nerovnosť už nie je uspokojená. Iba ak n=6 nerovnosť platí, takže pre indukčný základ môžeme brať n=6.
Predpokladajme, že nerovnosť platí pre nejaké prirodzené Komu:
Posledná nerovnosť platí ak 
2) 
3)
; 4) 
.
Grécke písmeno "sigma".
:
4) 
2)
f
(
n
)=
n
2
+
n
+11
, o n=1,2,3,4,5,6,7
dá sa predpokladať, že pre akékoľvek prírodnéPčíslo f
(
n
)
jednoduché.
nie je prvočíslo pre žiadne prirodzené čísloP.
nasleduje pravda identity 
; 
. Takže táto identita platí pre všetkýchP
.
pre n≥2.
.
deleno 6
bez stopy.
.
viacnásobný6.
viacnásobný6
.
na5
bez stopy.
.
tiež rozdelené na5
bez stopy.
na16.
viacnásobný16.
na676.
deleno 
.
.
deleno26
.
deleno26
2
.
deleno5
bez stopy.
deleno5.
deleno5
bez stopy.
deleno6
bez stopy.
deleno6
bez stopy.
deleno6
bez stopy.
párne číslo.
pri delení podľa9
dáva zvyšok 1
.
deleno9
.
deleno 9
. Nechajte pri n=k
deleno9
.
viacnásobný5
(dokázané v príklade č. 21), štvrtý a piaty člen sú tiež násobky5
, čo je zrejmé, potom je súčet násobkom15
.
.
- správny.
je skutočná nerovnosť.
pre akékoľvek P.
.
pri 
potom
pre akékoľvek prírodné P a akékoľvek 
, správny.
.
pre akékoľvek prírodné P.
Vynásobte obe strany nerovnosti o 
. Získame ekvivalentnú nerovnosť resp 
; 
; - táto nerovnosť platí pre všetky prírodné T.
; 
; 
.
.
, potom pre všetky prírodné hodnotyP
nerovnosť
a zjavne správne. Predpokladajme, že je to pravdan=k
, toto je čo 
.
, potom 
, a preto nerovnosť nemení svoj význam, keď sa obe jej časti vynásobia o 
:
, potom to dostaneme
.
Zvážte nerovnosť
Testová práca na tému n=1 sa uvádza opakovane: n≥5 , kde P- -prirodzené číslo.
